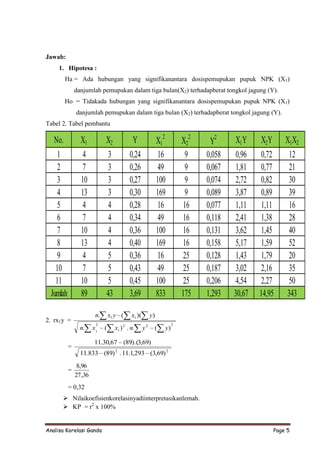
Analisa Korelasi Ganda memberikan ringkasan tentang:
1. Korelasi ganda antara dosis pupuk NPK, jumlah pemupukan, dan berat tongkol jagung.
2. Terdapat hubungan yang signifikan antara ketiga variabel tersebut.
3. Koefisien korelasi ganda sangat kuat sebesar 0,87.