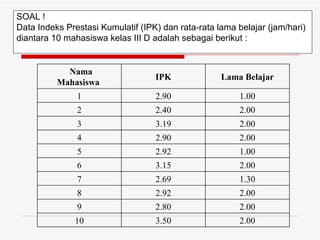
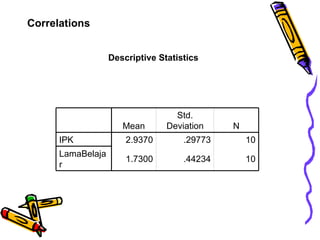
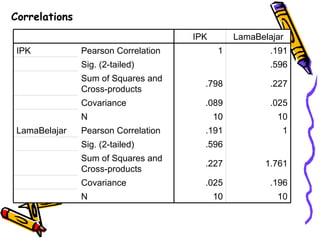
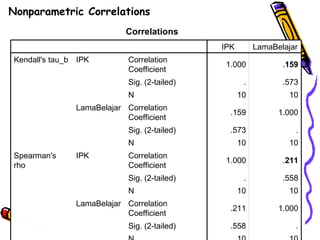
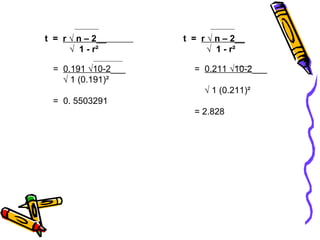Dokumen ini membahas uji korelasi yang sering digunakan dalam penelitian, termasuk bivariate correlation dan partial correlation. Koefisien korelasi 'r' mengukur kekuatan hubungan antara dua variabel, dengan nilai berkisar antara -1 hingga +1. Penilaian hasil 'r' dilakukan melalui besarnya nilai dan pengujian probabilitas untuk menentukan keberadaan korelasi yang signifikan.

1. Korelasi Uji korelasi banyak digunakan dalam berbagai penelitian, dari yang sederhana hingga penelitian yang cukup kompleks. Uji korelasi yang banyak digunakan antara lain : Uji Korelasi Sederhana (Bivariate Correlation) dan korelasi Parsial (Partial Correlation) dari Person Product Moument.

2. BIVARIATE CORRELATION Bivariate Correlation (korelasi sederhana) bermanfaat untuk menghasilkan matrik korelasi pasangan antar 2 variabel. Pada umumnya, orang mengatakan bahwa pengertian korelasi adalah suatu hubungan timbal-balik. Contohnya, hubungan antara permintaan dan penawaran, hubungan antara motivasi dan prestasi belajar, dll. Dimana kedua hubungan tersebut bisa saling mempengaruhinya. Namun, pada kenyataannya tidak semua hubungan terjadi saling menimbulkan sebab akibat. Oleh karena itu, perlu diperhatikan benar apakah hubungan itu merupakan hubungan timbal-balik atau bukan.

3. Keeratan hubungan antara satu variabel dengan variabel lainnya, biasa disebut dengan koofisien korelasi yang ditandai dengan ”r”. Koofisien korelasi ”r” merupakan taksiran dari korelasi populasi dengan kondisi sample normal (acak). Adapun rumus r, sebagai berikut : r = (N – 1) SxSy

4. Tingkat keeratan hubungan (koofisien korelasi) bergerak dari 0-1. jika r mendekati 1 (misalnya 0.95) ini dapat dikatakan bahwa memiliki hubungan yang sangat erat. Sebaliknya, jika mendekati 0 (misalnya 0.10) dapat dikatakan mempunyai hubungan yang rendah. Koofisien korelasi mempunyai harga -1 hingga +1. harga -1 menunjukan adanya hubungan yang sempurna bersifat terbalik antara kedua variabel. Sedangkan hubungan +1 menunjukan adanya hubungan sempurna positif.

5. Penilaian terhadap hasil ”r” dapat dilakukan dengan beberapa cara, diantaranya : Dengan cara melihat besarnya nilai “r”. Sebab, semakin besar nilai “r”, yakni semakin mendekati angka 1. seperti berikut ini 0 – 0.20 sangat rendah 0.21 - 0.40 rendah 0.41 - 0.60 sedang 0.61 - 0.80 cukup tinggi 0.81 - 1 tinggi

6. Dapat pula dilakukan dengan pengujian probabilitas dari hasil “r”. Jika probabilitas r > 0.05, berarti Ho : diterima (tidak dapat korelasi) Jika probabilitas r < 0.05, berarti Ho : ditolak (terdapat korelasi yang berarti) Dapat pula dilakukan dengan pengujian t-tes.

7. SOAL ! Data Indeks Prestasi Kumulatif (IPK) dan rata-rata lama belajar (jam/hari) diantara 10 mahasiswa kelas III D adalah sebagai berikut : 2.00 3.50 10 2.00 2.80 9 2.00 2.92 8 1.30 2.69 7 2.00 3.15 6 1.00 2.92 5 2.00 2.90 4 2.00 3.19 3 2.00 2.40 2 1.00 2.90 1 Lama Belajar IPK Nama Mahasiswa

8. Correlations Descriptive Statistics 10 .44234 1.7300 LamaBelajar 10 .29773 2.9370 IPK N Std. Deviation Mean

9. Correlations 10 10 N .196 .025 Covariance 1.761 .227 Sum of Squares and Cross-products .596 Sig. (2-tailed) 1 .191 Pearson Correlation LamaBelajar 10 10 N .025 .089 Covariance .227 .798 Sum of Squares and Cross-products .596 Sig. (2-tailed) .191 1 Pearson Correlation IPK LamaBelajar IPK

10. ANALISIS OUTPUT Dari output diperoleh informasi sebagai berikut : Mean dari IPK = 2.9370 Mean dari Lama Belajar = 1.7300 Standar deviasi IPK = 0.29773 Standar deviasi Lama belajar = 0.44234 Banyaknya data yang dianalisis = 10 Dengan menggunakan korelasi Pearson diperoleh : r = 0 .191

11. Nonparametric Correlations Correlations 10 10 N . .558 Sig. (2-tailed) 1.000 .211 Correlation Coefficient LamaBelajar 10 10 N .558 . Sig. (2-tailed) . 211 1.000 Correlation Coefficient IPK Spearman's rho 10 10 N . .573 Sig. (2-tailed) 1.000 .159 Correlation Coefficient LamaBelajar 10 10 N .573 . Sig. (2-tailed) . 159 1.000 Correlation Coefficient IPK Kendall's tau_b LamaBelajar IPK

12. t = r √ n – 2 __ √ 1 - r² = 0.191 √10-2 ___ √ 1 (0.191)² = 0. 5503291 t = r √ n – 2 __ √ 1 - r² = 0.211 √10-2 ___ √ 1 (0.211)² = 2.828