Janet Stemwedel, profile picture
Uploaded byJanet Stemwedel
PPT, PDF2,637 views

Truth table analysis

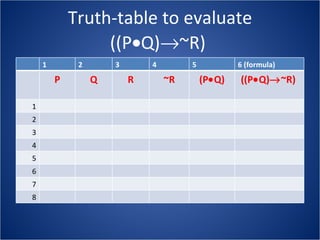
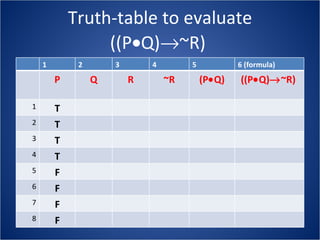
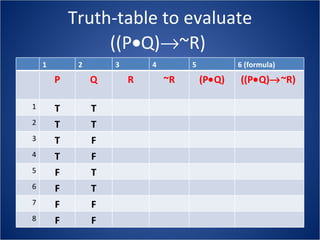
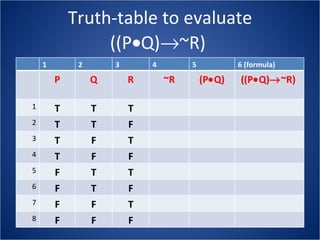
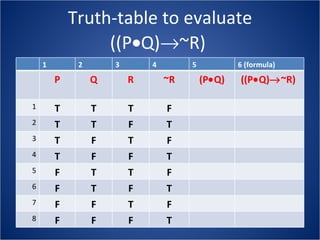
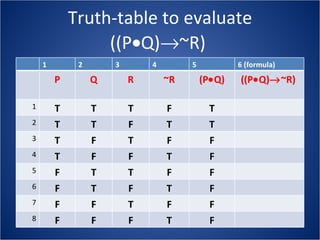
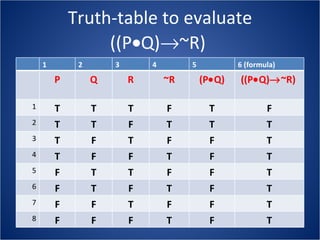
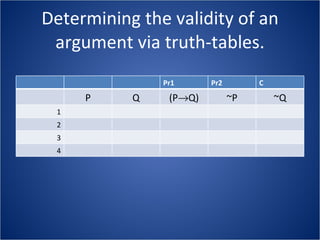
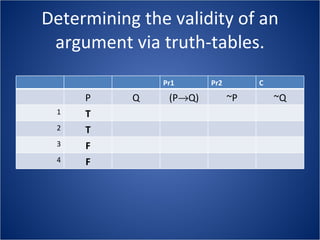
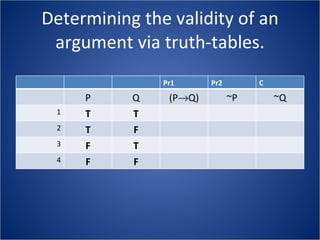
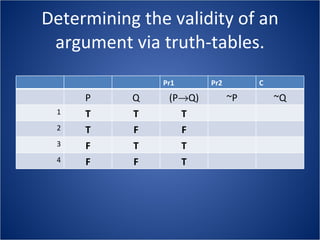
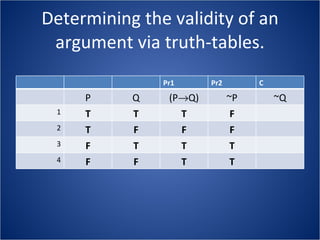
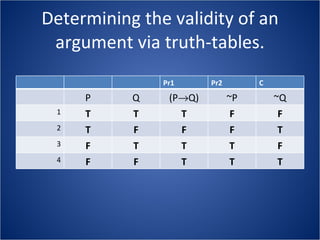
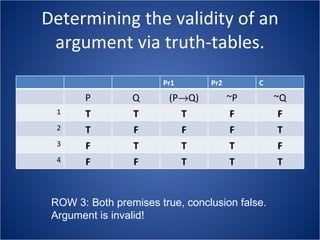
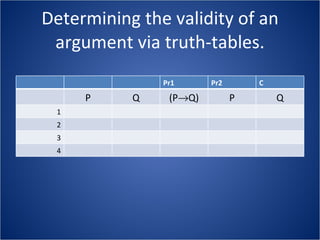
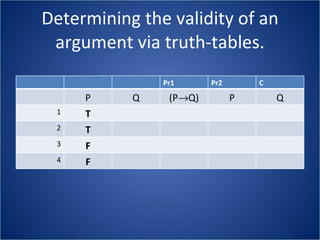
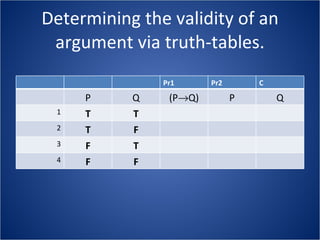
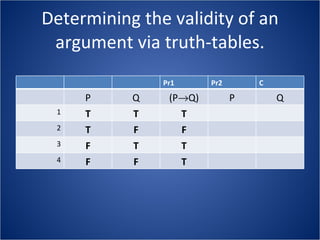
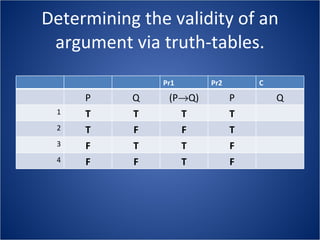
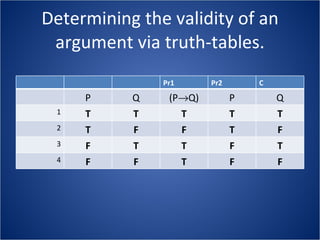
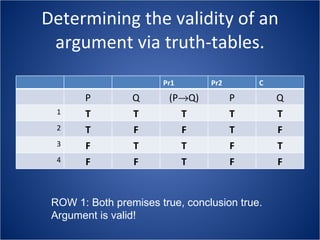
The document discusses how truth tables can be used to determine the logical status of propositions and arguments. Truth tables assign truth values (True/False) to propositions based on the truth values of their component statements, allowing the logical status of single propositions and groups of propositions to be determined. The logical status can be tautology, contradiction, contingent, equivalent, satisfiable/consistent, or unsatisfiable/inconsistent depending on the truth values. Validity of arguments can also be determined from truth tables by checking if the conclusion is true in all rows where the premises are true. Examples of truth tables are provided to illustrate these concepts.

Embed presentation

Downloaded 85 times
Truth-Table Analysis Phil 57 section 3 San Jose State University Fall 2010
What are truth-tables good for? Working out the truth value of a formula from the truth values of the atomic formulae in it. Defining the behavior of logical connectives used to build complex formulae.
What are truth-tables good for? Determining the logical status of a single proposition. Determining the logical status of a group of propositions. Determining the validity of an argument.
The logical status of a proposition. Some propositions are always true: It will rain or it won’t. Some propositions are never true: The universe is empty and not empty. Most propositions are true in some conditions and false in others: Today is hot.
The logical status of a proposition. Can use truth-tables to distinguish these different kinds of propositions. Logical status Description Truth-Table Tautology Always true Every row T Contradiction Always false Every row F Contingent Depends on circumstances Some row T, some row F
The logical status of a proposition. Consider P  ~P P ~P P  ~P
The logical status of a proposition. Consider P  ~P P ~P P  ~P T F
The logical status of a proposition. Consider P  ~P P ~P P  ~P T F F T
The logical status of a proposition. Consider P  ~P P ~P P  ~P T F F F T F
The logical status of a proposition. Consider P  ~P Truth-value for P  ~P is F in every row. (Contradiction) P ~P P  ~P T F F F T F
The logical status of a proposition. Consider P  ~P P ~P P  ~P
The logical status of a proposition. Consider P  ~P P ~P P  ~P T F
The logical status of a proposition. Consider P  ~P P ~P P  ~P T F F T
The logical status of a proposition. Consider P  ~P P ~P P  ~P T F T F T T
The logical status of a proposition. Consider P  ~P Truth-value for P  ~P is T in every row. (Tautology) P ~P P  ~P T F T F T T
The logical status of a group of propositions. Do two different claims mean the same thing? Can two different claims both be true? Must one of a pair of claims be false if the other is true?
The logical status of a group of propositions. Logical Status Description Truth-Table Equivalent Mean the same thing, logically The truth-tables are identical Satisfiable/consistent Possibly all true. There is some row where all propositions are true. Unsatisfiable/inconsistent Can’t all be true. No row where all propositions are true.
Rules for building truth-tables: As many columns as: Statement letters Non-atomic formulae The formula to be computed 2 N rows, where N= number of atomic statement letters.
Truth-table to evaluate ((P  Q)  ~R) 1 2 3 4 5 6 (formula) P Q R ~R (P  Q) ((P  Q)  ~R) 1 2 3 4 5 6 7 8
Truth-table to evaluate ((P  Q)  ~R) 1 2 3 4 5 6 (formula) P Q R ~R (P  Q) ((P  Q)  ~R) 1 T 2 T 3 T 4 T 5 F 6 F 7 F 8 F
Truth-table to evaluate ((P  Q)  ~R) 1 2 3 4 5 6 (formula) P Q R ~R (P  Q) ((P  Q)  ~R) 1 T T 2 T T 3 T F 4 T F 5 F T 6 F T 7 F F 8 F F
Truth-table to evaluate ((P  Q)  ~R) 1 2 3 4 5 6 (formula) P Q R ~R (P  Q) ((P  Q)  ~R) 1 T T T 2 T T F 3 T F T 4 T F F 5 F T T 6 F T F 7 F F T 8 F F F
Truth-table to evaluate ((P  Q)  ~R) 1 2 3 4 5 6 (formula) P Q R ~R (P  Q) ((P  Q)  ~R) 1 T T T F 2 T T F T 3 T F T F 4 T F F T 5 F T T F 6 F T F T 7 F F T F 8 F F F T
Truth-table to evaluate ((P  Q)  ~R) 1 2 3 4 5 6 (formula) P Q R ~R (P  Q) ((P  Q)  ~R) 1 T T T F T 2 T T F T T 3 T F T F F 4 T F F T F 5 F T T F F 6 F T F T F 7 F F T F F 8 F F F T F
Truth-table to evaluate ((P  Q)  ~R) 1 2 3 4 5 6 (formula) P Q R ~R (P  Q) ((P  Q)  ~R) 1 T T T F T F 2 T T F T T T 3 T F T F F T 4 T F F T F T 5 F T T F F T 6 F T F T F T 7 F F T F F T 8 F F F T F T
Determining the logical status of (~P  P) 1 2 3 (formula) P ~P (~P  P) 1 2
Determining the logical status of (~P  P) 1 2 3 (formula) P ~P (~P  P) 1 T 2 F
Determining the logical status of (~P  P) 1 2 3 (formula) P ~P (~P  P) 1 T F 2 F T
Determining the logical status of (~P  P) 1 2 3 (formula) P ~P (~P  P) 1 T F T 2 F T F
Determining the logical status of (~P  P) Formula is CONTINGENT. 1 2 3 (formula) P ~P (~P  P) 1 T F T 2 F T F
Determining the logical status of (P  ~Q) 1 2 3 4 P Q ~Q (P  ~Q) 1 2 3 4
Determining the logical status of (P  ~Q) 1 2 3 4 P Q ~Q (P  ~Q) 1 T 2 T 3 F 4 F
Determining the logical status of (P  ~Q) 1 2 3 4 P Q ~Q (P  ~Q) 1 T T 2 T F 3 F T 4 F F
Determining the logical status of (P  ~Q) 1 2 3 4 P Q ~Q (P  ~Q) 1 T T F 2 T F T 3 F T F 4 F F T
Determining the logical status of (P  ~Q) 1 2 3 4 P Q ~Q (P  ~Q) 1 T T F F 2 T F T T 3 F T F F 4 F F T F
Steps for determining logical status of a proposition. Create truth-table with right number of rows and columns. Compute truth-value of every formula on every row using truth-values of atomic statements for the row. Check for the logical status by checking the relevant rows.
The logical status of a proposition. Can use truth-tables to distinguish these different kinds of propositions. Logical status Description Truth-Table Tautology Always true Every row T Contradiction Always false Every row F Contingent Depends on circumstances Some row T, some row F
Determining the logical status of a group of propositions. Build truth-table to give side-by-side comparison of the truth values of the propositions. Doing this in a single truth-table is the best way to ensure an apples-to-apples comparison.
Logical status of ~(P  Q), (~P  ~Q) 1 2 3 4 5 6 7 P Q ~P ~Q (P  Q) ~(P  Q) (~P  ~Q) 1 2 3 4
Logical status of ~(P  Q), (~P  ~Q) 1 2 3 4 5 6 7 P Q ~P ~Q (P  Q) ~(P  Q) (~P  ~Q) 1 T 2 T 3 F 4 F
Logical status of ~(P  Q), (~P  ~Q) 1 2 3 4 5 6 7 P Q ~P ~Q (P  Q) ~(P  Q) (~P  ~Q) 1 T T 2 T F 3 F T 4 F F
Logical status of ~(P  Q), (~P  ~Q) 1 2 3 4 5 6 7 P Q ~P ~Q (P  Q) ~(P  Q) (~P  ~Q) 1 T T F 2 T F F 3 F T T 4 F F T
Logical status of ~(P  Q), (~P  ~Q) 1 2 3 4 5 6 7 P Q ~P ~Q (P  Q) ~(P  Q) (~P  ~Q) 1 T T F F 2 T F F T 3 F T T F 4 F F T T
Logical status of ~(P  Q), (~P  ~Q) 1 2 3 4 5 6 7 P Q ~P ~Q (P  Q) ~(P  Q) (~P  ~Q) 1 T T F F T 2 T F F T F 3 F T T F F 4 F F T T F
Logical status of ~(P  Q), (~P  ~Q) 1 2 3 4 5 6 7 P Q ~P ~Q (P  Q) ~(P  Q) (~P  ~Q) 1 T T F F T F 2 T F F T F T 3 F T T F F T 4 F F T T F T
Logical status of ~(P  Q), (~P  ~Q) 1 2 3 4 5 6 7 P Q ~P ~Q (P  Q) ~(P  Q) (~P  ~Q) 1 T T F F T F F 2 T F F T F T T 3 F T T F F T T 4 F F T T F T T
Logical status of ~(P  Q), (~P  ~Q) Both formulae have the same truth-values on every row ( equivalent ) 1 2 3 4 5 6 7 P Q ~P ~Q (P  Q) ~(P  Q) (~P  ~Q) 1 T T F F T F F 2 T F F T F T T 3 F T T F F T T 4 F F T T F T T
Logical status of (P  Q), (P  Q) 1 2 3 4 P Q (P  Q) (P  Q) 1 2 3 4
Logical status of (P  Q), (P  Q) 1 2 3 4 P Q (P  Q) (P  Q) 1 T 2 T 3 F 4 F
Logical status of (P  Q), (P  Q) 1 2 3 4 P Q (P  Q) (P  Q) 1 T T 2 T F 3 F T 4 F F
Logical status of (P  Q), (P  Q) 1 2 3 4 P Q (P  Q) (P  Q) 1 T T T 2 T F F 3 F T F 4 F F F
Logical status of (P  Q), (P  Q) 1 2 3 4 P Q (P  Q) (P  Q) 1 T T T T 2 T F F T 3 F T F T 4 F F F F
Logical status of (P  Q), (P  Q) A row (1) where both formulae are T ( satisfiable, but not equivalent ) 1 2 3 4 P Q (P  Q) (P  Q) 1 T T T T 2 T F F T 3 F T F T 4 F F F F
Logical status of (P  ~Q), (P  Q) 1 2 3 4 P Q ~Q (P  ~Q) (P  Q) 1 2 3 4
Logical status of (P  ~Q), (P  Q) 1 2 3 4 P Q ~Q (P  ~Q) (P  Q) 1 T 2 T 3 F 4 F
Logical status of (P  ~Q), (P  Q) 1 2 3 4 P Q ~Q (P  ~Q) (P  Q) 1 T T 2 T F 3 F T 4 F F
Logical status of (P  ~Q), (P  Q) 1 2 3 4 P Q ~Q (P  ~Q) (P  Q) 1 T T F 2 T F T 3 F T F 4 F F T
Logical status of (P  ~Q), (P  Q) 1 2 3 4 P Q ~Q (P  ~Q) (P  Q) 1 T T F F 2 T F T T 3 F T F T 4 F F T T
Logical status of (P  ~Q), (P  Q) 1 2 3 4 P Q ~Q (P  ~Q) (P  Q) 1 T T F F T 2 T F T T F 3 F T F T F 4 F F T T F
Logical status of (P  ~Q), (P  Q) NO row where both formulae are T ( unsatisfiable ) 1 2 3 4 P Q ~Q (P  ~Q) (P  Q) 1 T T F F T 2 T F T T F 3 F T F T F 4 F F T T F
Steps for determining logical status of group of propositions. Create truth-table with right number of rows and columns. Compute truth-value of every formula on every row using truth-values of atomic statements for the row. Check for the logical status by checking the relevant rows.
The logical status of a group of propositions. Logical Status Description Truth-Table Equivalent Mean the same thing, logically The truth-tables are identical Satisfiable/consistent Possibly all true. There is some row where all propositions are true. Unsatisfiable/inconsistent Can’t all be true. No row where all propositions are true.
Determining the validity of an argument via truth-tables. Remember that a valid argument is one where, if all the premises are true, the conclusion must be true.
Determining the validity of an argument via truth-tables. Remember that a valid argument is one where, if all the premises are true, the conclusion must be true. Build truth table that includes formulae for premises and conclusion.
Determining the validity of an argument via truth-tables. Remember that a valid argument is one where, if all the premises are true, the conclusion must be true. Build truth table that includes formulae for premises and conclusion. If there’s a row where the premises are true and the conclusion is false, argument is invalid .
Determining the validity of an argument via truth-tables. Remember that a valid argument is one where, if all the premises are true, the conclusion must be true. Build truth table that includes formulae for premises and conclusion. If there’s a row where the premises are true and the conclusion is false, argument is invalid . Otherwise, argument is valid.
Determining the validity of an argument via truth-tables. If John wins the election, then Mary will run for Governor. John did not win the election. (Conclusion) So, Mary will not run for Governor.
Determining the validity of an argument via truth-tables. If John wins the election, then Mary will run for Governor. John did not win the election. (Conclusion) So, Mary will not run for Governor. P = John wins the election. Q = Mary will run for Governor.
Determining the validity of an argument via truth-tables. If John wins the election, then Mary will run for Governor. (P  Q) John did not win the election. ~P (Conclusion) So, Mary will not run for Governor. ~Q P = John wins the election. Q = Mary will run for Governor.
Determining the validity of an argument via truth-tables. Pr1 Pr2 C P Q (P  Q) ~P ~Q 1 2 3 4
Determining the validity of an argument via truth-tables. Pr1 Pr2 C P Q (P  Q) ~P ~Q 1 T 2 T 3 F 4 F
Determining the validity of an argument via truth-tables. Pr1 Pr2 C P Q (P  Q) ~P ~Q 1 T T 2 T F 3 F T 4 F F
Determining the validity of an argument via truth-tables. Pr1 Pr2 C P Q (P  Q) ~P ~Q 1 T T T 2 T F F 3 F T T 4 F F T
Determining the validity of an argument via truth-tables. Pr1 Pr2 C P Q (P  Q) ~P ~Q 1 T T T F 2 T F F F 3 F T T T 4 F F T T
Determining the validity of an argument via truth-tables. Pr1 Pr2 C P Q (P  Q) ~P ~Q 1 T T T F F 2 T F F F T 3 F T T T F 4 F F T T T
Determining the validity of an argument via truth-tables. ROW 3: Both premises true, conclusion false. Argument is invalid! Pr1 Pr2 C P Q (P  Q) ~P ~Q 1 T T T F F 2 T F F F T 3 F T T T F 4 F F T T T
Determining the validity of an argument via truth-tables. If John wins the election, then Mary will run for Governor. John won the election. (Conclusion) So, Mary will run for Governor. P = John wins the election. Q = Mary will run for Governor.
Determining the validity of an argument via truth-tables. If John wins the election, then Mary will run for Governor. (P  Q) John won the election. P (Conclusion) So, Mary will run for Governor. Q P = John wins the election. Q = Mary will run for Governor.
Determining the validity of an argument via truth-tables. Pr1 Pr2 C P Q (P  Q) P Q 1 2 3 4
Determining the validity of an argument via truth-tables. Pr1 Pr2 C P Q (P  Q) P Q 1 T 2 T 3 F 4 F
Determining the validity of an argument via truth-tables. Pr1 Pr2 C P Q (P  Q) P Q 1 T T 2 T F 3 F T 4 F F
Determining the validity of an argument via truth-tables. Pr1 Pr2 C P Q (P  Q) P Q 1 T T T 2 T F F 3 F T T 4 F F T
Determining the validity of an argument via truth-tables. Pr1 Pr2 C P Q (P  Q) P Q 1 T T T T 2 T F F T 3 F T T F 4 F F T F
Determining the validity of an argument via truth-tables. Pr1 Pr2 C P Q (P  Q) P Q 1 T T T T T 2 T F F T F 3 F T T F T 4 F F T F F
Determining the validity of an argument via truth-tables. ROW 1: Both premises true, conclusion true. Argument is valid! Pr1 Pr2 C P Q (P  Q) P Q 1 T T T T T 2 T F F T F 3 F T T F T 4 F F T F F
Important note for homework: Some of the expressions you’ll be evaluating in truth-tables use alternate notation.  means ~  means   means 

More Related Content

PDF
permutations power point
byAldrin Balenton
 
PPT
Discrete Math Lecture 03: Methods of Proof
byIT Engineering Department
 
PPTX
2-3. MATHEMATICS AS A LANGUAGE.pptx
byYviAshena
 
PPTX
Chapter 2 Mathematics in the Modern World.pptx
byLitoDeGuia1
 
PPTX
Problem-Solving Strategies
byStephen Babbitt
 
DOCX
Cs6660 compiler design may june 2016 Answer Key
byappasami
 
PPTX
Branch and bound technique
byishmecse13
 
PPTX
B+ trees and height balance tree
byJasleen Kaur (Chandigarh University)
 
permutations power point
byAldrin Balenton
 
Discrete Math Lecture 03: Methods of Proof
byIT Engineering Department
 
2-3. MATHEMATICS AS A LANGUAGE.pptx
byYviAshena
 
Chapter 2 Mathematics in the Modern World.pptx
byLitoDeGuia1
 
Problem-Solving Strategies
byStephen Babbitt
 
Cs6660 compiler design may june 2016 Answer Key
byappasami
 
Branch and bound technique
byishmecse13
 
B+ trees and height balance tree
byJasleen Kaur (Chandigarh University)
 

What's hot

PPTX
Proposition
byrey castro
 
PPTX
Turing machine and Halting Introduction
byAmartyaYandrapu1
 
PPTX
DEONTOLOGY ETHICS.pptx
byacademicschool
 
PPTX
Political self . Understanding the self
byIvy Gomez
 
PDF
Searching and Sorting Techniques in Data Structure
byBalwant Gorad
 
PDF
Mathematical language-and-symbols-including-sets
byJutay Nicavera
 
PPTX
Merge Sort
byNikhil Sonkamble
 
PPTX
Permutations and combinations ppt
byPriya !!!
 
PPTX
Proposition (Logic)
byEFREN ARCHIDE
 
PPTX
Math 8 - Linear Inequalities in Two Variables
byCarlo Luna
 
PPTX
Strassen's matrix multiplication
byMegha V
 
PPTX
Universal values PowerPoint presentation
bySafna KV
 
PPT
Utilitarianism
byMamWamar_SHS Teacher/College Instructor at ESTI
 
PPTX
Permutations
byDINAVILLANUEVA3
 
PPTX
Chapter 4 logical reasoning
byJaypee Sidon
 
PPTX
Doubly Linked List
byNinad Mankar
 
PPTX
Job sequencing with Deadlines
byYashiUpadhyay3
 
PPT
Fundamentals of the Analysis of Algorithm Efficiency
bySaranya Natarajan
 
PPTX
Height balanced Tree
byNiveMurugan1
 
PPTX
Data Structures and Algorithm - Module 1.pptx
byEllenGrace9
 
Proposition
byrey castro
 
Turing machine and Halting Introduction
byAmartyaYandrapu1
 
DEONTOLOGY ETHICS.pptx
byacademicschool
 
Political self . Understanding the self
byIvy Gomez
 
Searching and Sorting Techniques in Data Structure
byBalwant Gorad
 
Mathematical language-and-symbols-including-sets
byJutay Nicavera
 
Merge Sort
byNikhil Sonkamble
 
Permutations and combinations ppt
byPriya !!!
 
Proposition (Logic)
byEFREN ARCHIDE
 
Math 8 - Linear Inequalities in Two Variables
byCarlo Luna
 
Strassen's matrix multiplication
byMegha V
 
Universal values PowerPoint presentation
bySafna KV
 
Utilitarianism
byMamWamar_SHS Teacher/College Instructor at ESTI
 
Permutations
byDINAVILLANUEVA3
 
Chapter 4 logical reasoning
byJaypee Sidon
 
Doubly Linked List
byNinad Mankar
 
Job sequencing with Deadlines
byYashiUpadhyay3
 
Fundamentals of the Analysis of Algorithm Efficiency
bySaranya Natarajan
 
Height balanced Tree
byNiveMurugan1
 
Data Structures and Algorithm - Module 1.pptx
byEllenGrace9
 

Viewers also liked

PPT
Indirect-table Analysis
byJanet Stemwedel
 
PPTX
IS 151 Lecture 3
bywajanga
 
PPT
Chap 10(structure and unions)
byBangabandhu Sheikh Mujibur Rahman Science and Technology University
 
PPT
IS 139 Lecture 7
bywajanga
 
PPTX
IS 151 - Lecture 3
bywajanga
 
PPTX
Chapter one
bykiran acharya
 
PPTX
IS 151 Lecture 2
bywajanga
 
PPT
Cd unit i
bythulasib1
 
PPT
pointer, structure ,union and intro to file handling
byRai University
 
PPTX
aaالمملكة العربية السعودية
byabdullah259
 
PPTX
Logical and Conditional Operator In C language
byAbdul Rehman
 
PPTX
C Structures and Unions
byDhrumil Patel
 
PPT
Logic gates
byprasanna chitra
 
PPTX
Hierarchical Memory System
byJenny Galino
 
PPT
C Structures & Unions
byRam Sagar Mourya
 
PPTX
Memory Hierarchy
byTrinity Dwarka
 
PPT
Truth tables
bywalkerlj
 
PPTX
Discrete math Truth Table
byUniversity of Potsdam
 
PPTX
C pointer
byUniversity of Potsdam
 
PDF
Introduction to compilers
byBilal Maqbool ツ
 
Indirect-table Analysis
byJanet Stemwedel
 
IS 151 Lecture 3
bywajanga
 
Chap 10(structure and unions)
byBangabandhu Sheikh Mujibur Rahman Science and Technology University
 
IS 139 Lecture 7
bywajanga
 
IS 151 - Lecture 3
bywajanga
 
Chapter one
bykiran acharya
 
IS 151 Lecture 2
bywajanga
 
Cd unit i
bythulasib1
 
pointer, structure ,union and intro to file handling
byRai University
 
aaالمملكة العربية السعودية
byabdullah259
 
Logical and Conditional Operator In C language
byAbdul Rehman
 
C Structures and Unions
byDhrumil Patel
 
Logic gates
byprasanna chitra
 
Hierarchical Memory System
byJenny Galino
 
C Structures & Unions
byRam Sagar Mourya
 
Memory Hierarchy
byTrinity Dwarka
 
Truth tables
bywalkerlj
 
Discrete math Truth Table
byUniversity of Potsdam
 
C pointer
byUniversity of Potsdam
 
Introduction to compilers
byBilal Maqbool ツ
 

Similar to Truth table analysis

PPTX
Logic - Logical Propositions
byJosefMikaeldelCorro
 
DOCX
LOGIC
byshahzadebaujiti
 
PPTX
Truth table
byLiwayway Memije-Cruz
 
PDF
Proposition Logic in Discrete Structure
byNANDINI SHARMA
 
PPTX
Constructiong Truth Table sfsdf sdfsf.pptx
byfermanrw
 
DOCX
Dicrete structure
byHoney Joy Macabasco
 
PPTX
Chapter1p1
byAngel Martinez
 
PDF
Logic
byAmit Kumar Rathi
 
PPT
Propositional And First-Order Logic
byankush_kumar
 
PDF
Logic and proof
bySuresh Ram
 
PPTX
Drinkfromme.pptx
byRavind8
 
PPT
IT1101 Mathematics for Computing II 2001
byGihan Wikramanayake
 
PPTX
PROPOSITIONAL Logic for students who study logic
bySeniorbLemhes
 
DOCX
Logic worksheet
byAlejandroBuhia
 
PPTX
logic_intro___logic_laws__bma18008_dr.p.sona.pptx
byJaikumarKittuswamy1
 
PPT
Logic
byLoida Silao
 
PPTX
Propositional Logics in Theoretical computer science
byAhmad177077
 
PPT
Mathematical foundations of computer science
byBindhuBhargaviTalasi
 
PPTX
Unit 1-logic
byraksharao
 
PDF
Chapter 01 - p1.pdf
bysmarwaneid
 
Logic - Logical Propositions
byJosefMikaeldelCorro
 
LOGIC
byshahzadebaujiti
 
Truth table
byLiwayway Memije-Cruz
 
Proposition Logic in Discrete Structure
byNANDINI SHARMA
 
Constructiong Truth Table sfsdf sdfsf.pptx
byfermanrw
 
Dicrete structure
byHoney Joy Macabasco
 
Chapter1p1
byAngel Martinez
 
Logic
byAmit Kumar Rathi
 
Propositional And First-Order Logic
byankush_kumar
 
Logic and proof
bySuresh Ram
 
Drinkfromme.pptx
byRavind8
 
IT1101 Mathematics for Computing II 2001
byGihan Wikramanayake
 
PROPOSITIONAL Logic for students who study logic
bySeniorbLemhes
 
Logic worksheet
byAlejandroBuhia
 
logic_intro___logic_laws__bma18008_dr.p.sona.pptx
byJaikumarKittuswamy1
 
Logic
byLoida Silao
 
Propositional Logics in Theoretical computer science
byAhmad177077
 
Mathematical foundations of computer science
byBindhuBhargaviTalasi
 
Unit 1-logic
byraksharao
 
Chapter 01 - p1.pdf
bysmarwaneid
 

More from Janet Stemwedel

PPT
Climategate and scientific methodology
byJanet Stemwedel
 
PPT
P160 Kuhn and his Critics
byJanet Stemwedel
 
PPT
P160 Duhem and Quine
byJanet Stemwedel
 
PPT
P160 Hempel, Hume, Deduction, and Induction
byJanet Stemwedel
 
PPT
Lect10 Human Subjects: History
byJanet Stemwedel
 
PPT
Lect11 Human Subjects: Regulations
byJanet Stemwedel
 
PPT
Lec12 Human Subjects:Global Issues
byJanet Stemwedel
 
PPT
Lec13 Scientific Papers and Communications
byJanet Stemwedel
 
PPT
Lec 14 Authorship Issues
byJanet Stemwedel
 
PPT
Lec15 Patents and Intellectual Property
byJanet Stemwedel
 
PPT
Lec16 International Strategies for Scientific Dialogue
byJanet Stemwedel
 
PPT
Explanation classroomversion
byJanet Stemwedel
 
PPT
P160 antirealismclassroomversion
byJanet Stemwedel
 
PPT
P160 naturalismclassroomlect
byJanet Stemwedel
 
PPT
Feminist Critiques of Science
byJanet Stemwedel
 
PPT
Translating English to Propositional Logic
byJanet Stemwedel
 
PPT
P160 Kuhn classroom Lecture 2
byJanet Stemwedel
 
PPT
Propositional logic
byJanet Stemwedel
 
PPT
Kuhn: Paradigms and Normal Science
byJanet Stemwedel
 
PPT
Syntax and semantics of propositional logic
byJanet Stemwedel
 
Climategate and scientific methodology
byJanet Stemwedel
 
P160 Kuhn and his Critics
byJanet Stemwedel
 
P160 Duhem and Quine
byJanet Stemwedel
 
P160 Hempel, Hume, Deduction, and Induction
byJanet Stemwedel
 
Lect10 Human Subjects: History
byJanet Stemwedel
 
Lect11 Human Subjects: Regulations
byJanet Stemwedel
 
Lec12 Human Subjects:Global Issues
byJanet Stemwedel
 
Lec13 Scientific Papers and Communications
byJanet Stemwedel
 
Lec 14 Authorship Issues
byJanet Stemwedel
 
Lec15 Patents and Intellectual Property
byJanet Stemwedel
 
Lec16 International Strategies for Scientific Dialogue
byJanet Stemwedel
 
Explanation classroomversion
byJanet Stemwedel
 
P160 antirealismclassroomversion
byJanet Stemwedel
 
P160 naturalismclassroomlect
byJanet Stemwedel
 
Feminist Critiques of Science
byJanet Stemwedel
 
Translating English to Propositional Logic
byJanet Stemwedel
 
P160 Kuhn classroom Lecture 2
byJanet Stemwedel
 
Propositional logic
byJanet Stemwedel
 
Kuhn: Paradigms and Normal Science
byJanet Stemwedel
 
Syntax and semantics of propositional logic
byJanet Stemwedel
 

Recently uploaded

PPTX
Lesson_1 Acceleration.pptx_Science 8-4th quarter
byAnnabelAlarcon
 
PPTX
EYE IRRIGATION AND INSTILLATION....pptx
byAneetaSharma15
 
PDF
Using T-Test to Analyze Research Data.pdf
byThelma Villaflores
 
PPTX
A detailed notes on Conjugate Vaccine and its mechanism.
byDr. R. Ram
 
PPTX
MEMORY &FORGETTING. Shilpa Hotakar.Psychology pptx
bySHILPA HOTAKAR
 
PDF
Bones by Sadu Kassam (play) story ppt pdf
byRonnieMaeBorres
 
PDF
Judgement Regarding Land Acquisition Act not Applicable to Encroachers.pdf
byssuser9d8e4e
 
PPTX
G5_ENGLISH_PPT_Q4_W2.pptx week 2 quarter 4
by96zn2w5tqx
 
PPTX
SOLAR SYSTEM.pptx || The infinity solar system
bymahadevdigital024
 
PPTX
A brief introduction to Minor vegetable crops.pptx
byUmeshTimilsina1
 
PPTX
Math 8 Quarter 4 Week 4-SECONDARY DATA.pptx
byshahanieabbat3
 
PPTX
How Physician Assistants in the USA Earn CME Credits Online.pptx
byCME4Life
 
PDF
Pratishta Educational Society., Courses & Opportunities
byGanapathiVankudoth
 
PPTX
ENGLISH-7-Quarter-4-Week-3 Matatag .pptx
byKimberlyJadeCuyos
 
PDF
Why Projects Fail – The Need to “Do the Right Project” and “Do the Project Ri...
byAssociation for Project Management
 
PPTX
World cancer day 2026 4febuary united by unique
byDr Santosh Vishwakarma
 
DOCX
Q4_-LE_PEH8_Lesson1_Week1 pls don't docx
bymirajaneee00
 
PDF
Tetracycline Class of Antibiotics: SAR, MOA and Uses
bymominzarinamdnajeeb
 
PDF
Chapter 05 Drugs Acting on the Central Nervous System: Anticonvulsant (Antiep...
bySandeshSul
 
PDF
RAJAT ARORA SIR PHYSICAL EDUCATION NOTES ALL CHAPTERS .pdf
bysumitkannoujiya74
 
Lesson_1 Acceleration.pptx_Science 8-4th quarter
byAnnabelAlarcon
 
EYE IRRIGATION AND INSTILLATION....pptx
byAneetaSharma15
 
Using T-Test to Analyze Research Data.pdf
byThelma Villaflores
 
A detailed notes on Conjugate Vaccine and its mechanism.
byDr. R. Ram
 
MEMORY &FORGETTING. Shilpa Hotakar.Psychology pptx
bySHILPA HOTAKAR
 
Bones by Sadu Kassam (play) story ppt pdf
byRonnieMaeBorres
 
Judgement Regarding Land Acquisition Act not Applicable to Encroachers.pdf
byssuser9d8e4e
 
G5_ENGLISH_PPT_Q4_W2.pptx week 2 quarter 4
by96zn2w5tqx
 
SOLAR SYSTEM.pptx || The infinity solar system
bymahadevdigital024
 
A brief introduction to Minor vegetable crops.pptx
byUmeshTimilsina1
 
Math 8 Quarter 4 Week 4-SECONDARY DATA.pptx
byshahanieabbat3
 
How Physician Assistants in the USA Earn CME Credits Online.pptx
byCME4Life
 
Pratishta Educational Society., Courses & Opportunities
byGanapathiVankudoth
 
ENGLISH-7-Quarter-4-Week-3 Matatag .pptx
byKimberlyJadeCuyos
 
Why Projects Fail – The Need to “Do the Right Project” and “Do the Project Ri...
byAssociation for Project Management
 
World cancer day 2026 4febuary united by unique
byDr Santosh Vishwakarma
 
Q4_-LE_PEH8_Lesson1_Week1 pls don't docx
bymirajaneee00
 
Tetracycline Class of Antibiotics: SAR, MOA and Uses
bymominzarinamdnajeeb
 
Chapter 05 Drugs Acting on the Central Nervous System: Anticonvulsant (Antiep...
bySandeshSul
 
RAJAT ARORA SIR PHYSICAL EDUCATION NOTES ALL CHAPTERS .pdf
bysumitkannoujiya74
 

Truth table analysis

  • 1.
    Truth-Table Analysis Phil57 section 3 San Jose State University Fall 2010
  • 2.
    What are truth-tablesgood for? Working out the truth value of a formula from the truth values of the atomic formulae in it. Defining the behavior of logical connectives used to build complex formulae.
  • 3.
    What are truth-tablesgood for? Determining the logical status of a single proposition. Determining the logical status of a group of propositions. Determining the validity of an argument.
  • 4.
    The logical statusof a proposition. Some propositions are always true: It will rain or it won’t. Some propositions are never true: The universe is empty and not empty. Most propositions are true in some conditions and false in others: Today is hot.
  • 5.
    The logical statusof a proposition. Can use truth-tables to distinguish these different kinds of propositions. Logical status Description Truth-Table Tautology Always true Every row T Contradiction Always false Every row F Contingent Depends on circumstances Some row T, some row F
  • 6.
    The logical statusof a proposition. Consider P  ~P P ~P P  ~P
  • 7.
    The logical statusof a proposition. Consider P  ~P P ~P P  ~P T F
  • 8.
    The logical statusof a proposition. Consider P  ~P P ~P P  ~P T F F T
  • 9.
    The logical statusof a proposition. Consider P  ~P P ~P P  ~P T F F F T F
  • 10.
    The logical statusof a proposition. Consider P  ~P Truth-value for P  ~P is F in every row. (Contradiction) P ~P P  ~P T F F F T F
  • 11.
    The logical statusof a proposition. Consider P  ~P P ~P P  ~P
  • 12.
    The logical statusof a proposition. Consider P  ~P P ~P P  ~P T F
  • 13.
    The logical statusof a proposition. Consider P  ~P P ~P P  ~P T F F T
  • 14.
    The logical statusof a proposition. Consider P  ~P P ~P P  ~P T F T F T T
  • 15.
    The logical statusof a proposition. Consider P  ~P Truth-value for P  ~P is T in every row. (Tautology) P ~P P  ~P T F T F T T
  • 16.
    The logical statusof a group of propositions. Do two different claims mean the same thing? Can two different claims both be true? Must one of a pair of claims be false if the other is true?
  • 17.
    The logical statusof a group of propositions. Logical Status Description Truth-Table Equivalent Mean the same thing, logically The truth-tables are identical Satisfiable/consistent Possibly all true. There is some row where all propositions are true. Unsatisfiable/inconsistent Can’t all be true. No row where all propositions are true.
  • 18.
    Rules for buildingtruth-tables: As many columns as: Statement letters Non-atomic formulae The formula to be computed 2 N rows, where N= number of atomic statement letters.
  • 19.
    Truth-table to evaluate((P  Q)  ~R) 1 2 3 4 5 6 (formula) P Q R ~R (P  Q) ((P  Q)  ~R) 1 2 3 4 5 6 7 8
  • 20.
    Truth-table to evaluate((P  Q)  ~R) 1 2 3 4 5 6 (formula) P Q R ~R (P  Q) ((P  Q)  ~R) 1 T 2 T 3 T 4 T 5 F 6 F 7 F 8 F
  • 21.
    Truth-table to evaluate((P  Q)  ~R) 1 2 3 4 5 6 (formula) P Q R ~R (P  Q) ((P  Q)  ~R) 1 T T 2 T T 3 T F 4 T F 5 F T 6 F T 7 F F 8 F F
  • 22.
    Truth-table to evaluate((P  Q)  ~R) 1 2 3 4 5 6 (formula) P Q R ~R (P  Q) ((P  Q)  ~R) 1 T T T 2 T T F 3 T F T 4 T F F 5 F T T 6 F T F 7 F F T 8 F F F
  • 23.
    Truth-table to evaluate((P  Q)  ~R) 1 2 3 4 5 6 (formula) P Q R ~R (P  Q) ((P  Q)  ~R) 1 T T T F 2 T T F T 3 T F T F 4 T F F T 5 F T T F 6 F T F T 7 F F T F 8 F F F T
  • 24.
    Truth-table to evaluate((P  Q)  ~R) 1 2 3 4 5 6 (formula) P Q R ~R (P  Q) ((P  Q)  ~R) 1 T T T F T 2 T T F T T 3 T F T F F 4 T F F T F 5 F T T F F 6 F T F T F 7 F F T F F 8 F F F T F
  • 25.
    Truth-table to evaluate((P  Q)  ~R) 1 2 3 4 5 6 (formula) P Q R ~R (P  Q) ((P  Q)  ~R) 1 T T T F T F 2 T T F T T T 3 T F T F F T 4 T F F T F T 5 F T T F F T 6 F T F T F T 7 F F T F F T 8 F F F T F T
  • 26.
    Determining the logicalstatus of (~P  P) 1 2 3 (formula) P ~P (~P  P) 1 2
  • 27.
    Determining the logicalstatus of (~P  P) 1 2 3 (formula) P ~P (~P  P) 1 T 2 F
  • 28.
    Determining the logicalstatus of (~P  P) 1 2 3 (formula) P ~P (~P  P) 1 T F 2 F T
  • 29.
    Determining the logicalstatus of (~P  P) 1 2 3 (formula) P ~P (~P  P) 1 T F T 2 F T F
  • 30.
    Determining the logicalstatus of (~P  P) Formula is CONTINGENT. 1 2 3 (formula) P ~P (~P  P) 1 T F T 2 F T F
  • 31.
    Determining the logicalstatus of (P  ~Q) 1 2 3 4 P Q ~Q (P  ~Q) 1 2 3 4
  • 32.
    Determining the logicalstatus of (P  ~Q) 1 2 3 4 P Q ~Q (P  ~Q) 1 T 2 T 3 F 4 F
  • 33.
    Determining the logicalstatus of (P  ~Q) 1 2 3 4 P Q ~Q (P  ~Q) 1 T T 2 T F 3 F T 4 F F
  • 34.
    Determining the logicalstatus of (P  ~Q) 1 2 3 4 P Q ~Q (P  ~Q) 1 T T F 2 T F T 3 F T F 4 F F T
  • 35.
    Determining the logicalstatus of (P  ~Q) 1 2 3 4 P Q ~Q (P  ~Q) 1 T T F F 2 T F T T 3 F T F F 4 F F T F
  • 36.
    Steps for determininglogical status of a proposition. Create truth-table with right number of rows and columns. Compute truth-value of every formula on every row using truth-values of atomic statements for the row. Check for the logical status by checking the relevant rows.
  • 37.
    The logical statusof a proposition. Can use truth-tables to distinguish these different kinds of propositions. Logical status Description Truth-Table Tautology Always true Every row T Contradiction Always false Every row F Contingent Depends on circumstances Some row T, some row F
  • 38.
    Determining the logicalstatus of a group of propositions. Build truth-table to give side-by-side comparison of the truth values of the propositions. Doing this in a single truth-table is the best way to ensure an apples-to-apples comparison.
  • 39.
    Logical status of~(P  Q), (~P  ~Q) 1 2 3 4 5 6 7 P Q ~P ~Q (P  Q) ~(P  Q) (~P  ~Q) 1 2 3 4
  • 40.
    Logical status of~(P  Q), (~P  ~Q) 1 2 3 4 5 6 7 P Q ~P ~Q (P  Q) ~(P  Q) (~P  ~Q) 1 T 2 T 3 F 4 F
  • 41.
    Logical status of~(P  Q), (~P  ~Q) 1 2 3 4 5 6 7 P Q ~P ~Q (P  Q) ~(P  Q) (~P  ~Q) 1 T T 2 T F 3 F T 4 F F
  • 42.
    Logical status of~(P  Q), (~P  ~Q) 1 2 3 4 5 6 7 P Q ~P ~Q (P  Q) ~(P  Q) (~P  ~Q) 1 T T F 2 T F F 3 F T T 4 F F T
  • 43.
    Logical status of~(P  Q), (~P  ~Q) 1 2 3 4 5 6 7 P Q ~P ~Q (P  Q) ~(P  Q) (~P  ~Q) 1 T T F F 2 T F F T 3 F T T F 4 F F T T
  • 44.
    Logical status of~(P  Q), (~P  ~Q) 1 2 3 4 5 6 7 P Q ~P ~Q (P  Q) ~(P  Q) (~P  ~Q) 1 T T F F T 2 T F F T F 3 F T T F F 4 F F T T F
  • 45.
    Logical status of~(P  Q), (~P  ~Q) 1 2 3 4 5 6 7 P Q ~P ~Q (P  Q) ~(P  Q) (~P  ~Q) 1 T T F F T F 2 T F F T F T 3 F T T F F T 4 F F T T F T
  • 46.
    Logical status of~(P  Q), (~P  ~Q) 1 2 3 4 5 6 7 P Q ~P ~Q (P  Q) ~(P  Q) (~P  ~Q) 1 T T F F T F F 2 T F F T F T T 3 F T T F F T T 4 F F T T F T T
  • 47.
    Logical status of~(P  Q), (~P  ~Q) Both formulae have the same truth-values on every row ( equivalent ) 1 2 3 4 5 6 7 P Q ~P ~Q (P  Q) ~(P  Q) (~P  ~Q) 1 T T F F T F F 2 T F F T F T T 3 F T T F F T T 4 F F T T F T T
  • 48.
    Logical status of(P  Q), (P  Q) 1 2 3 4 P Q (P  Q) (P  Q) 1 2 3 4
  • 49.
    Logical status of(P  Q), (P  Q) 1 2 3 4 P Q (P  Q) (P  Q) 1 T 2 T 3 F 4 F
  • 50.
    Logical status of(P  Q), (P  Q) 1 2 3 4 P Q (P  Q) (P  Q) 1 T T 2 T F 3 F T 4 F F
  • 51.
    Logical status of(P  Q), (P  Q) 1 2 3 4 P Q (P  Q) (P  Q) 1 T T T 2 T F F 3 F T F 4 F F F
  • 52.
    Logical status of(P  Q), (P  Q) 1 2 3 4 P Q (P  Q) (P  Q) 1 T T T T 2 T F F T 3 F T F T 4 F F F F
  • 53.
    Logical status of(P  Q), (P  Q) A row (1) where both formulae are T ( satisfiable, but not equivalent ) 1 2 3 4 P Q (P  Q) (P  Q) 1 T T T T 2 T F F T 3 F T F T 4 F F F F
  • 54.
    Logical status of(P  ~Q), (P  Q) 1 2 3 4 P Q ~Q (P  ~Q) (P  Q) 1 2 3 4
  • 55.
    Logical status of(P  ~Q), (P  Q) 1 2 3 4 P Q ~Q (P  ~Q) (P  Q) 1 T 2 T 3 F 4 F
  • 56.
    Logical status of(P  ~Q), (P  Q) 1 2 3 4 P Q ~Q (P  ~Q) (P  Q) 1 T T 2 T F 3 F T 4 F F
  • 57.
    Logical status of(P  ~Q), (P  Q) 1 2 3 4 P Q ~Q (P  ~Q) (P  Q) 1 T T F 2 T F T 3 F T F 4 F F T
  • 58.
    Logical status of(P  ~Q), (P  Q) 1 2 3 4 P Q ~Q (P  ~Q) (P  Q) 1 T T F F 2 T F T T 3 F T F T 4 F F T T
  • 59.
    Logical status of(P  ~Q), (P  Q) 1 2 3 4 P Q ~Q (P  ~Q) (P  Q) 1 T T F F T 2 T F T T F 3 F T F T F 4 F F T T F
  • 60.
    Logical status of(P  ~Q), (P  Q) NO row where both formulae are T ( unsatisfiable ) 1 2 3 4 P Q ~Q (P  ~Q) (P  Q) 1 T T F F T 2 T F T T F 3 F T F T F 4 F F T T F
  • 61.
    Steps for determininglogical status of group of propositions. Create truth-table with right number of rows and columns. Compute truth-value of every formula on every row using truth-values of atomic statements for the row. Check for the logical status by checking the relevant rows.
  • 62.
    The logical statusof a group of propositions. Logical Status Description Truth-Table Equivalent Mean the same thing, logically The truth-tables are identical Satisfiable/consistent Possibly all true. There is some row where all propositions are true. Unsatisfiable/inconsistent Can’t all be true. No row where all propositions are true.
  • 63.
    Determining the validityof an argument via truth-tables. Remember that a valid argument is one where, if all the premises are true, the conclusion must be true.
  • 64.
    Determining the validityof an argument via truth-tables. Remember that a valid argument is one where, if all the premises are true, the conclusion must be true. Build truth table that includes formulae for premises and conclusion.
  • 65.
    Determining the validityof an argument via truth-tables. Remember that a valid argument is one where, if all the premises are true, the conclusion must be true. Build truth table that includes formulae for premises and conclusion. If there’s a row where the premises are true and the conclusion is false, argument is invalid .
  • 66.
    Determining the validityof an argument via truth-tables. Remember that a valid argument is one where, if all the premises are true, the conclusion must be true. Build truth table that includes formulae for premises and conclusion. If there’s a row where the premises are true and the conclusion is false, argument is invalid . Otherwise, argument is valid.
  • 67.
    Determining the validityof an argument via truth-tables. If John wins the election, then Mary will run for Governor. John did not win the election. (Conclusion) So, Mary will not run for Governor.
  • 68.
    Determining the validityof an argument via truth-tables. If John wins the election, then Mary will run for Governor. John did not win the election. (Conclusion) So, Mary will not run for Governor. P = John wins the election. Q = Mary will run for Governor.
  • 69.
    Determining the validityof an argument via truth-tables. If John wins the election, then Mary will run for Governor. (P  Q) John did not win the election. ~P (Conclusion) So, Mary will not run for Governor. ~Q P = John wins the election. Q = Mary will run for Governor.
  • 70.
    Determining the validityof an argument via truth-tables. Pr1 Pr2 C P Q (P  Q) ~P ~Q 1 2 3 4
  • 71.
    Determining the validityof an argument via truth-tables. Pr1 Pr2 C P Q (P  Q) ~P ~Q 1 T 2 T 3 F 4 F
  • 72.
    Determining the validityof an argument via truth-tables. Pr1 Pr2 C P Q (P  Q) ~P ~Q 1 T T 2 T F 3 F T 4 F F
  • 73.
    Determining the validityof an argument via truth-tables. Pr1 Pr2 C P Q (P  Q) ~P ~Q 1 T T T 2 T F F 3 F T T 4 F F T
  • 74.
    Determining the validityof an argument via truth-tables. Pr1 Pr2 C P Q (P  Q) ~P ~Q 1 T T T F 2 T F F F 3 F T T T 4 F F T T
  • 75.
    Determining the validityof an argument via truth-tables. Pr1 Pr2 C P Q (P  Q) ~P ~Q 1 T T T F F 2 T F F F T 3 F T T T F 4 F F T T T
  • 76.
    Determining the validityof an argument via truth-tables. ROW 3: Both premises true, conclusion false. Argument is invalid! Pr1 Pr2 C P Q (P  Q) ~P ~Q 1 T T T F F 2 T F F F T 3 F T T T F 4 F F T T T
  • 77.
    Determining the validityof an argument via truth-tables. If John wins the election, then Mary will run for Governor. John won the election. (Conclusion) So, Mary will run for Governor. P = John wins the election. Q = Mary will run for Governor.
  • 78.
    Determining the validityof an argument via truth-tables. If John wins the election, then Mary will run for Governor. (P  Q) John won the election. P (Conclusion) So, Mary will run for Governor. Q P = John wins the election. Q = Mary will run for Governor.
  • 79.
    Determining the validityof an argument via truth-tables. Pr1 Pr2 C P Q (P  Q) P Q 1 2 3 4
  • 80.
    Determining the validityof an argument via truth-tables. Pr1 Pr2 C P Q (P  Q) P Q 1 T 2 T 3 F 4 F
  • 81.
    Determining the validityof an argument via truth-tables. Pr1 Pr2 C P Q (P  Q) P Q 1 T T 2 T F 3 F T 4 F F
  • 82.
    Determining the validityof an argument via truth-tables. Pr1 Pr2 C P Q (P  Q) P Q 1 T T T 2 T F F 3 F T T 4 F F T
  • 83.
    Determining the validityof an argument via truth-tables. Pr1 Pr2 C P Q (P  Q) P Q 1 T T T T 2 T F F T 3 F T T F 4 F F T F
  • 84.
    Determining the validityof an argument via truth-tables. Pr1 Pr2 C P Q (P  Q) P Q 1 T T T T T 2 T F F T F 3 F T T F T 4 F F T F F
  • 85.
    Determining the validityof an argument via truth-tables. ROW 1: Both premises true, conclusion true. Argument is valid! Pr1 Pr2 C P Q (P  Q) P Q 1 T T T T T 2 T F F T F 3 F T T F T 4 F F T F F
  • 86.
    Important note forhomework: Some of the expressions you’ll be evaluating in truth-tables use alternate notation.  means ~  means   means 