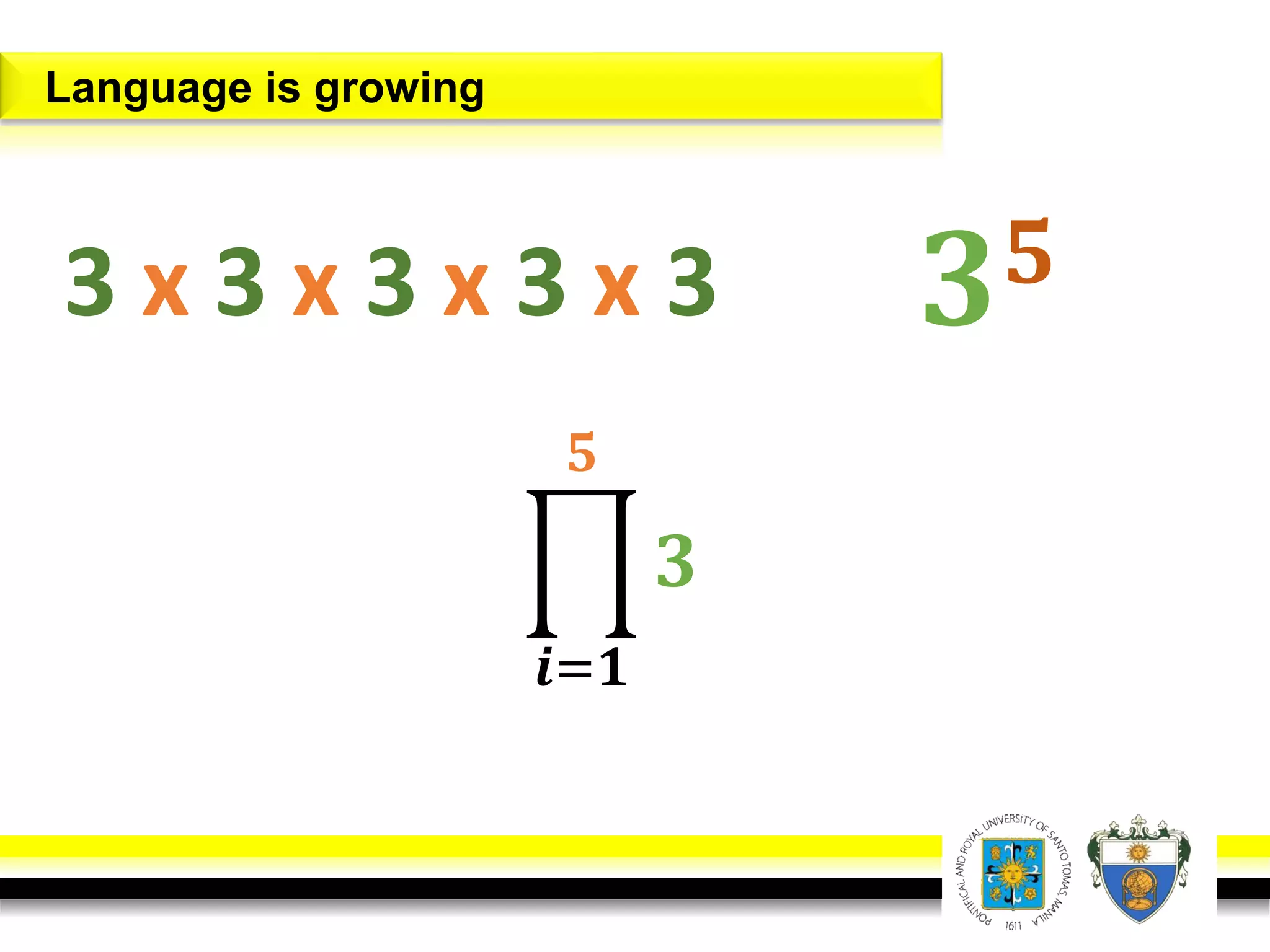
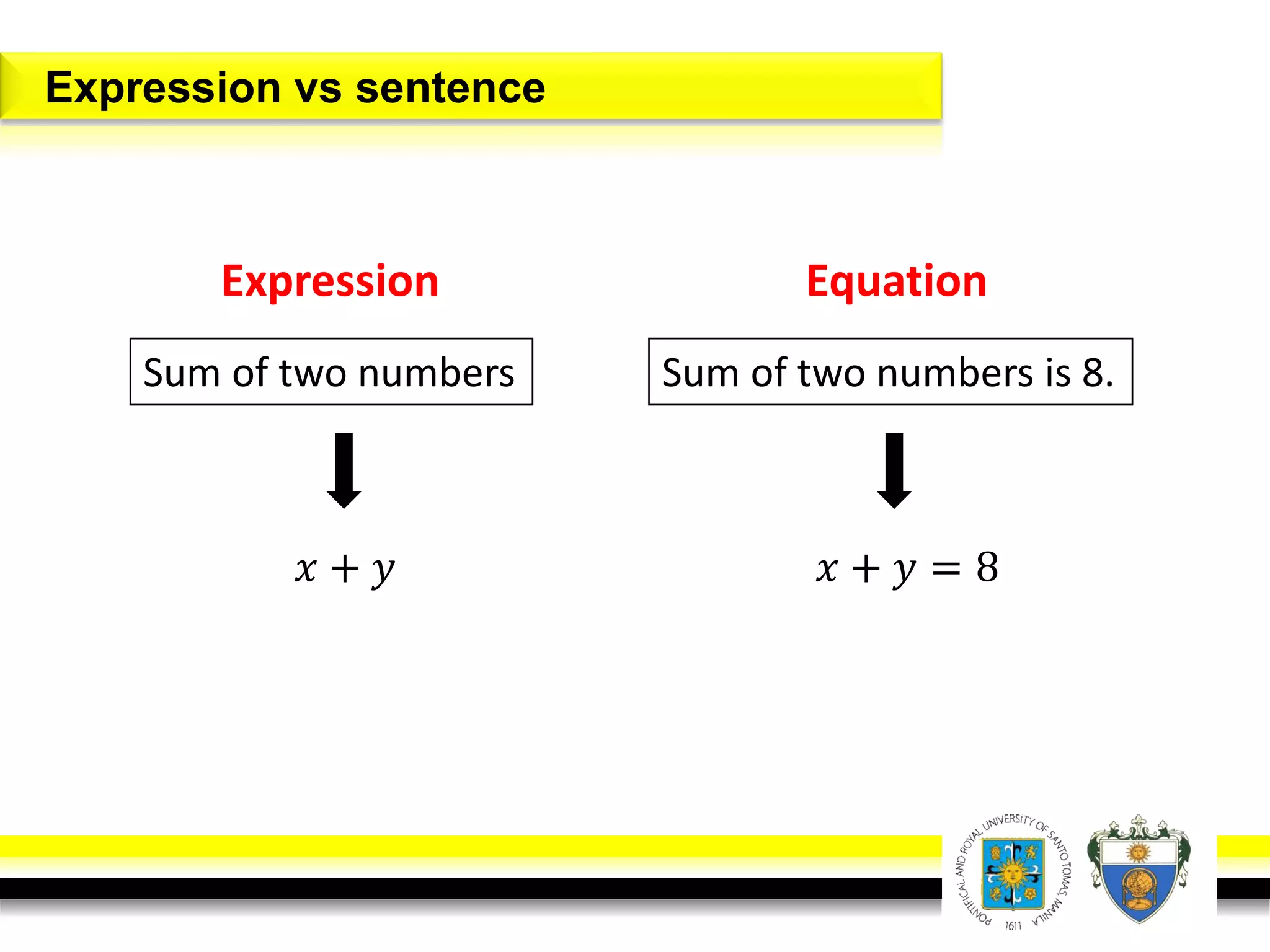
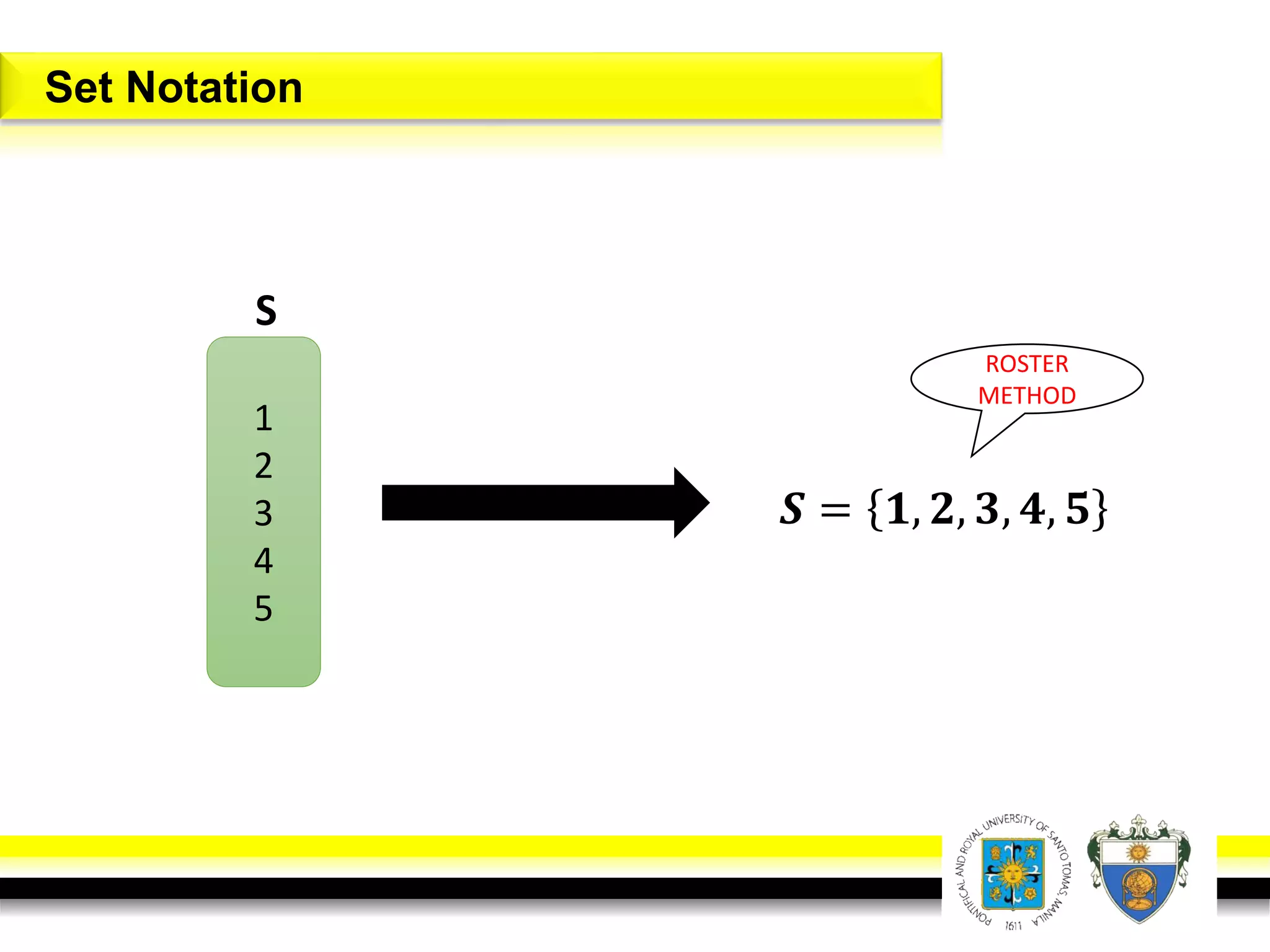
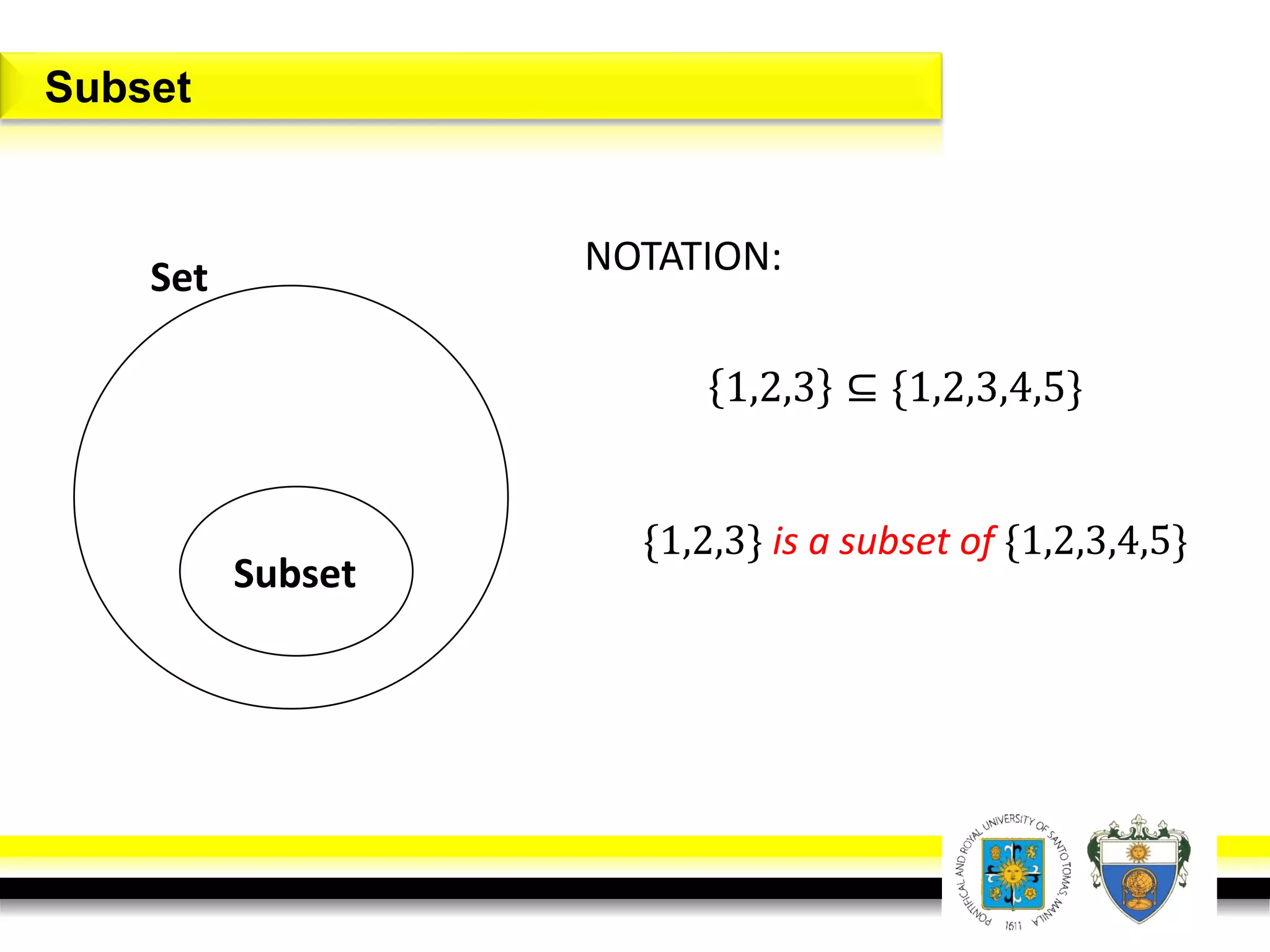
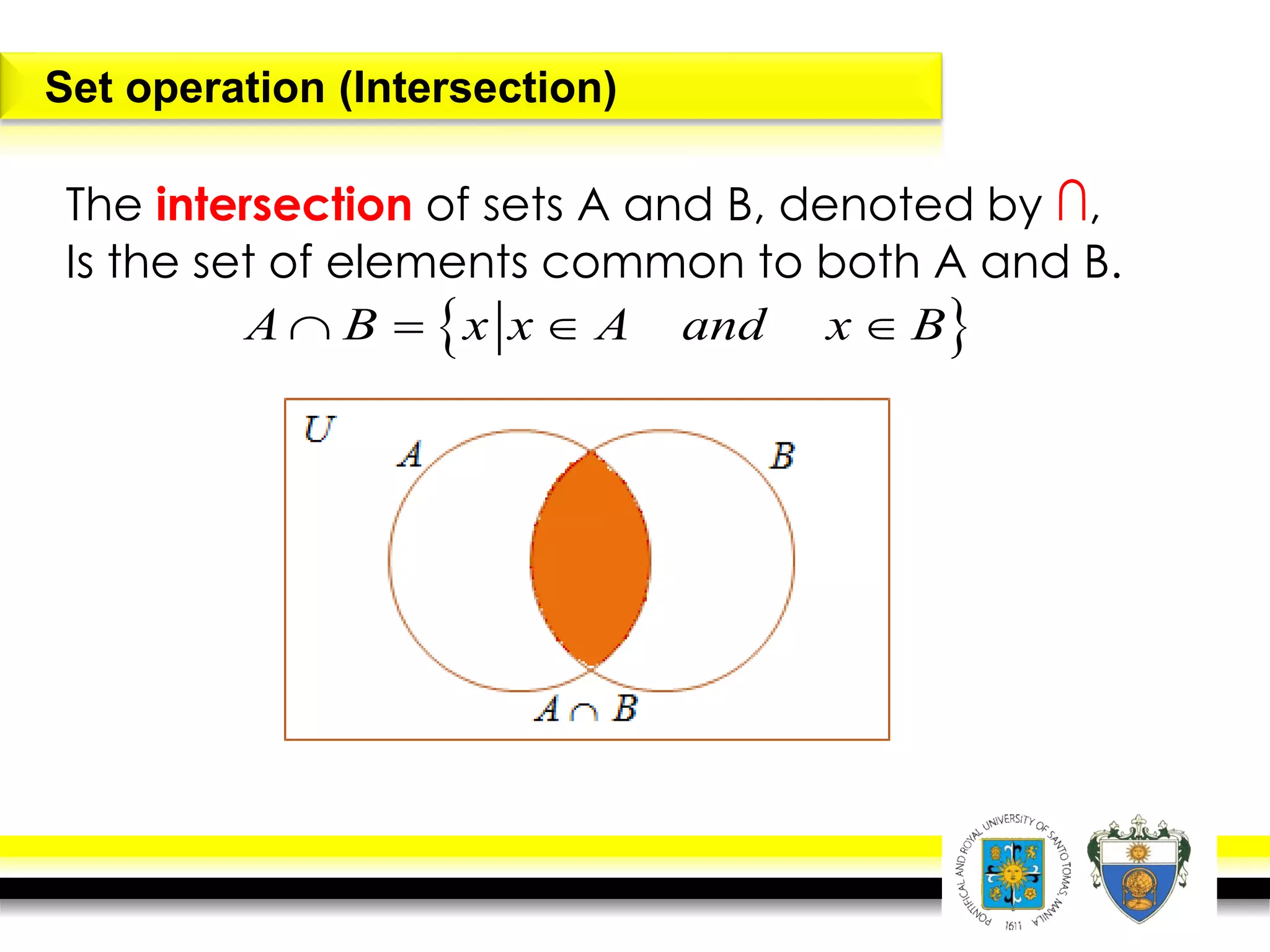
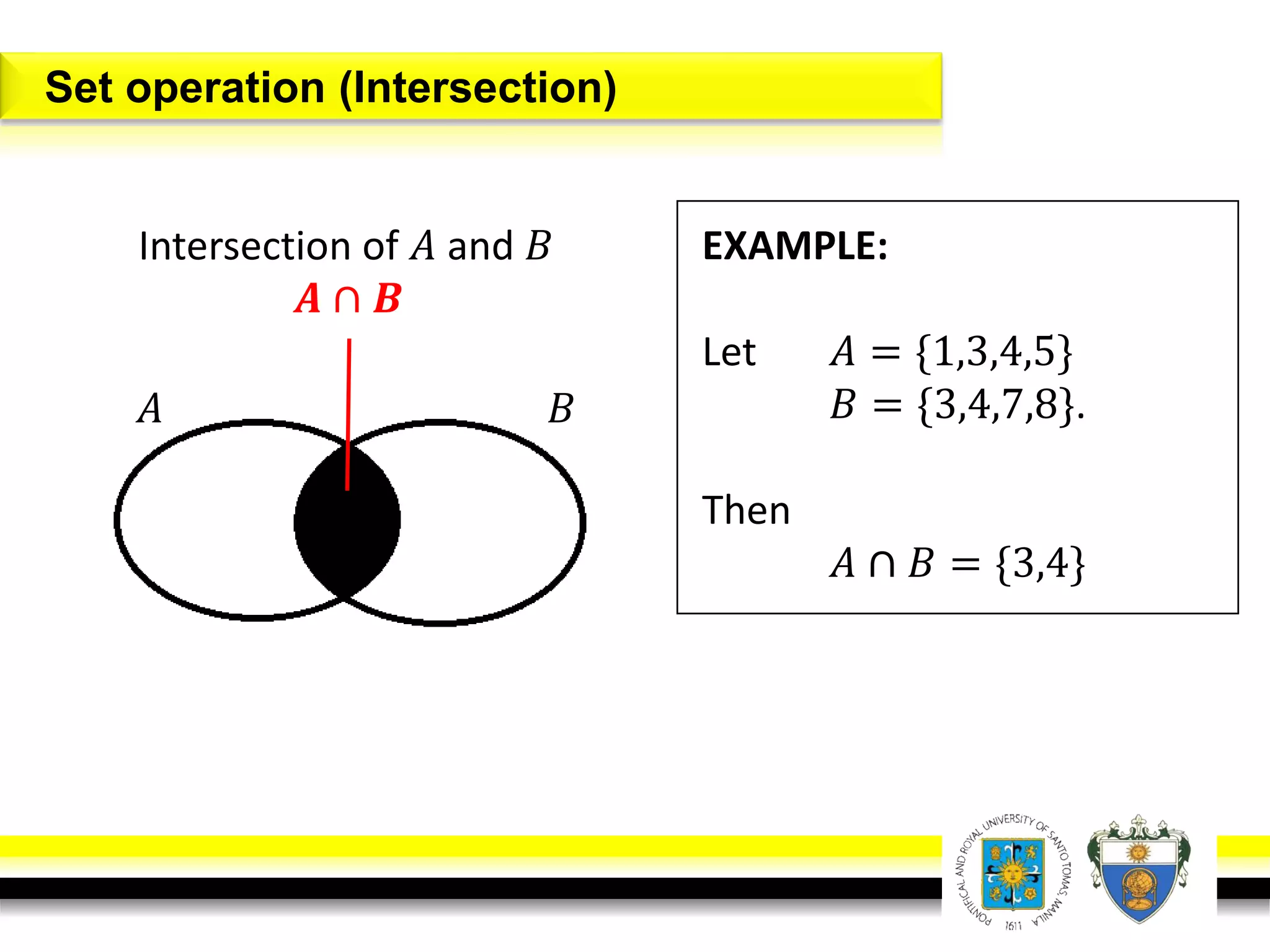
This document provides an overview of mathematical language and symbols. It discusses how mathematics can be considered a language with its own precise, concise and powerful means of communicating ideas using symbols. Examples of common symbols are presented, as well as how English phrases can be translated into mathematical expressions. Sets are then introduced as collections of objects or elements that can be represented using set notation. Operations on sets like union, intersection and complement are defined along with examples.

1. Mathematics in the Modern World – UNIT 2
Mathematical Language
& Symbols
Department of Mathematics and Physics
University of Santo Tomas
Prepared by Eugenio Cedric T. Corro
and Xandro Alexi A. Nieto

2. IS MATHEMATICS A
LANGUAGE?

3. What is a language?
Language (n.): a
systematic means of
communicating ideas or
feelings by the use of
conventional symbols,
sounds, or marks having
understood meaning

4. What is a language?

5. What is a language?
± ∞ ∅
𝒙 𝛉, 𝛃, 𝛜, 𝛔

6. What is a language?
∀
∃
∴
෍ 𝒙 , ෑ 𝒑 𝒙 , න 𝒇(𝒙) ,
‘for every”
“there exists”
“therefore”
sum, product, integral

7. Language is growing
3 x 3 x 3 x 3 x 3 𝟑 𝟓
ෑ
𝒊=𝟏
𝟓
𝟑

8. Phrasea group of words that expresses a concept
Sentencea group of words that are put together to
mean something

9. Expressiona group of number or variable
with or without mathematical operation
Equationa group of number or variable
with or without mathematical operation
separated by an equal sign

10. Expression vs sentence
Sum of two numbers
Expression
𝑥 + 𝑦

11. Expression vs sentence
Sum of two numbers is 8.
Equation
𝑥 + 𝑦 = 8
Sum of two numbers
Expression
𝑥 + 𝑦

12. Translate the
following to
mathematical
expressions
/equations.

13. English words to mathematics
English phrase/sentence Mathematical symbols
Product of two numbers 𝐴 × 𝐵 or 𝐴𝐵
Three more than twice a number 2𝑥 + 3
Two less than half a number is 15. 1
2
𝑦 − 2 = 15
The sum of three distinct numbers is at
least 10.
𝑥 + 𝑦 + 𝑧 ≥ 10
He owns at most eight cars. 𝐶 ≤ 8
The price of the house increased by 8%. 𝑃𝑛𝑒𝑤 = 𝑃𝑜𝑙𝑑 + 0.08 𝑃𝑜𝑙𝑑
Each kid gets one-eighth of the cake.
𝐾 =
1
8
𝐶

14. Expression or sentence?
Classify.
(1) The product of two numbers
(2) The sum of three integers is greater than 11.
(3) Half of the sum of 23 and 88
(4) The sum of two numbers is half their product.
(5) 2𝑥 − 3
(6) 𝑥 = 1
(7) 𝑥 +
3𝑦
2
(8) 𝑥 + 2𝑥 + 3𝑥 + 4𝑥 + 5𝑥

15. Characteristics of math language
• Precise
- able to make very fine distinctions
• Concise
- able to say things briefly
• Powerful
- able to express complex thoughts with
relative ease

16. Mathematics in the Modern World – UNIT 2
SETS

17. Mathematics in the Modern World – UNIT 2
SETS
collection of objects,
called as elements

18. 1
2
3
4
5
S
𝑺 = 𝟏, 𝟐, 𝟑, 𝟒, 𝟓
ROSTER
METHOD
Set Notation

19. 𝑺 = 𝟏, 𝟐, 𝟑, 𝟒, 𝟓
1 ∈ 𝑆 means “1 is an element of set 𝑆”
while
6 ∉ 𝑆 means “6 is NOT an element of set 𝑆”
Set Notation

20. 𝑺 = 𝟏, 𝟐, 𝟑, 𝟒, 𝟓, …
𝑆 also contains 6,7,8, and so on – all positive integers
Set Notation

21. 𝑻 = … , −𝟑, −𝟐, −𝟏
𝑇 also contains -4,-5,-6, and so on – all negative integers
Set Notation

22. 𝒁 = … , −𝟐, −𝟏, 𝟎, 𝟏, 𝟐, …
𝑍 also contains all integers
Set Notation

23. What if I want to know the set containing
ALL real numbers between 0 and 1
(including 0 and 1)?
Set Notation
𝑆 = 𝑥 | 𝑥 ≥ 0 𝐴𝑁𝐷 𝑥 ≤ 1
“such that”
“𝑆 contains all 𝑥’s such that 𝑥 is greater than or equal to 0 AND
𝑥 is less than or equal to 1”
Set-builder
notation

24. What if I want to know the set containing
ALL real numbers between 0 and 1
(including 0 and 1)?
Set Notation
𝑆 = 𝑥 | 𝑥 ≥ 0 ∩ 𝑥 ≤ 1

25. What if I want to know the set containing
ALL real numbers between 0 and 1
(including 0 and 1)?
Set Notation
𝑆 = 𝑥 | 0 ≤ 𝑥 ≤ 1

26. Set of natural numbers ℕ = 1, 2, 3, 4, 5, …
Set of integers ℤ = … , −2, −1, 0, 1, 2, …
Some known sets
Empty set ∅ or

27. Describe each set.
• {Sunday, Monday, Tuesday, Wednesday, Thursday,
Friday, Saturday}
• {A, E, I, O, U}
• {Mercury, Venus, Earth, Mars}
• {2, 4, 6, 8, 10}
• {2, 4, 6, 8, 10, …}
• {2, 3, 5, 7, 11, 13}
• {1, 4, 9, 16, 25}
Using sets

28. Write in set notation.
• Months with 31 days
• Colors of the rainbow
• Dog breeds that lay egg
• Three core Thomasian values
Using sets

29. 1. Explain why is incorrect.
2. Explain why is incorrect.
3. Consider the set . Does this set have
one or two elements? Explain.
   2 1,2,3
 1 1,2,3
  1, 1

30. Subset
Set
Subset
1,2,3 ⊆ {1,2,3,4,5}
NOTATION:
{1,2,3} is a subset of {1,2,3,4,5}

31. Subset (Examples and Nonexamples)
{1,2,3,4,5} is a subset of {1,2,3,4,5}.
{1,2} is a proper subset of {1,2,3,4,5}.
{6,7} is not a subset of {1,2,3,4,5}.
{1,3,6} is not a subset of {1,2,3,4,5}.
The empty set, ∅, is a subset of 1,2,3,4,5 .

32. Complement of a set
NOTATIONS: 𝐴 – any set
𝐴′ – the complement of set 𝐴
𝐴
𝐴′ The set 𝐴′ contains
elements in the
universal set which
are not contained
in set 𝐴.

33. Complement of a set (Examples)
Universal set → 𝐔 = {1,2,3,4,5,6,7,8,9,0}
If 𝐴 = 1,4,5,6 , then 𝐴′
= {2,3,7,8,9,0}.
If 𝐵 = {1,2,3}, then 𝐵′
= {4,5,6,7,8,9,0}.
If 𝐶 = {0,1,2,3,4,5,6,7,8,9}, then 𝐶′
= ∅

34. Set operation (Union)
The union of sets A and B, denoted by U, is the
set that contains all the elements that belong to A
or to B or to both.
 A B x x A or x B =  
U
A B
A B

35. Set operation (Union)
𝐴 𝐵
Union of 𝐴 and 𝐵
𝑨 ∪ 𝑩
EXAMPLE:
Let 𝐴 = {1,3,4,5}
𝐵 = {3,4,7,8}.
Then
𝐴 ∪ 𝐵 = {1,3,4,5,7,8}

36. Set operation (Intersection)
The intersection of sets A and B, denoted by ∩,
Is the set of elements common to both A and B.
 A B x x A and x B =  

37. Set operation (Intersection)
Intersection of 𝐴 and 𝐵
𝑨 ∩ 𝑩
EXAMPLE:
Let 𝐴 = {1,3,4,5}
𝐵 = {3,4,7,8}.
Then
𝐴 ∩ 𝐵 = {3,4}
𝐴 𝐵

38. LAST EXAMPLE:
Let U = {1,2,3,4,5,6,7,8,9,10,11,12}
A = 1,3,5,7,9,10
B = {1,2,3,5,7}
C = {2,4,6,7,8}
What is A∩(B∪ C)’?

39. NEXT TOPIC:
SETS OF FUNCTIONS
AND RELATIONS
& BINARY OPERATIONS