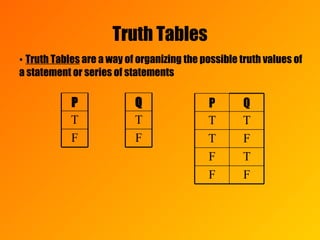
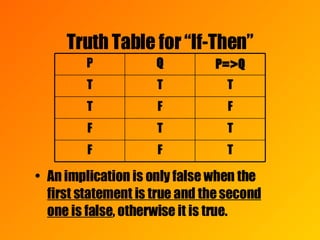
The document discusses different types of logical statements and their truth values. It defines simple and compound statements, truth tables, negation, conjunction, disjunction, implication, converse, and biconditional. Examples are provided to illustrate each concept, such as truth tables showing the possible truth value combinations of statements connected by logical operators like "and", "or", and "if-then".

1. Logic

2. Statements Statement – a sentence that is either true or false Examples: Lansing is the Capitol of Michigan All swimming pools are rectangles Mr. Cavis is an amazing teacher Class will be cancelled next Wednesday 2 is an even number 13 is an even number We often use ‘P’ or ‘Q’ to represent statements Ex – P 1 : Lansing is the Capitol of Michigan P 2 : All swimming pools are rectangles

3. Statements – Simple and Compound A Simple Statement is a statement that conveys 1 idea A Compound Statement is a statement that combines 2 or more simple statements Examples: Mr. Cavis drives a minivan Seven times four is 28 and today is Friday The earth is flat or I had waffles for breakfast

4. Truth Values and Open Sentences • A statement’s Truth Value is whether it is true (T) or false (F) • So P 1 : Lansing is the Capitol of Michigan has a truth value of true (T) • While P 2 : All swimming pools are rectangles, has a truth value of false (F) • Open sentence – a sentence whose truth value depends on the value of some variable. • Example: - 3x = 12; is a open math sentence.

5. Truth Tables • Truth Tables are a way of organizing the possible truth values of a statement or series of statements F T P F T Q F F T F F T T T Q P

6. Negation – “Not statements” • Negation – Changing a statement so that it has the opposite meaning and truth values - We generally do this by inserting the word ‘NOT’ - The symbol for negation is ‘~’ and is read “Not” - So if we have a statement P: five plus two is seven; the negation of that would be ~P: five plus two is not seven • Example: P: There is snow on the ground ~P: There is not snow on the ground

7. Truth Table for Negation F T P T F ~P

8. “ And Statements” (Conjunctions) When we are making the conjunction of 2 or more statements, we use the word “And,” and the symbol that we use is ‘^’ (Looks like an A without the middle line – ‘And’ starts with ‘A’) Example: P: I found $5 Q: I crashed my car into a telephone pole P^Q: I found $5 AND I crashed my car into a telephone pole .

9. Truth Table for “And” A conjunction is only true if all of the statements in it are true , otherwise it is false F F F F T F F F T T T T P^Q Q P

10. “ Or Statements” (Disjunctions) When we are making the disjunction of 2 or more statements, we use the word “Or,” and the symbol that we use is ‘ V ’ Example: P: The number 3 is odd Q: 57 is a prime number P V Q: The number 3 is odd OR 57 is a prime number .

11. Truth Table for “Or” A disjunction is true if at least one of the statements in it are true , otherwise it is false. F F F T T F T F T T T T P V Q Q P

12. Implication Called an implication because we are “Implying” something to be true Also known as an “If-Then” Statement An implication for statements P and Q is denoted P=> Q An implication is read either “If P, then Q” or “P implies Q”

13. Truth Table for “If-Then” An implication is only false when the first statement is true and the second one is false , otherwise it is true. T F F T T F F F T T T T P => Q Q P

14. Example of an “If-Then” Suppose a student in here is getting a B+ and asks me “Is there any way for me to get an ‘A’ in this class?” I tell that student “If you get an ‘A’ on the final exam, then you will get an ‘A’ in the class.” So here are our 2 statements *P: You get an ‘A’ on the Final Exam *Q: You get an ‘A’ in the class

15. Example of an “If-Then” (Cont.) Think of the combinations of outcomes as if I was telling the truth to that student or not and then consider the possible outcomes: Both P and Q are true - The student got an ‘A’ on the exam and then received an ‘A’ in the class - Therefore, I was telling the truth about the student’s final grade

16. Example of an “If-Then” (Cont.) 2) P is true, but Q is false - The student got an ‘A’ on the exam and then did not receive an ‘A’ in the class - Therefore, I was not telling the truth about the student’s final grade - What I said was false, which agrees with the 2 nd row of the truth table

17. Example of an “If-Then” (Cont.) 3) P is false and Q is true - The student did not get an ‘A’ on the exam (say they got a ‘B’) and then received an ‘A’ in the class - I did not lie when I spoke with the student initially, so I was telling the truth

18. Example of an “If-Then” (Cont.) 4) Both P and Q are false - The student did not get an ‘A’ on the exam and did not get an ‘A’ in the class - I only promised an ‘A’ in the class if the student got an ‘A’ on the exam, so again I was telling the truth, which agrees with the last row in the truth table.

19. Converse (Not the shoe brand) The converse is when you take an “If-Then” statement (P=>Q) and reverse the order of the statements (Q=>P) *So, Q=>P is the converse of P=>Q Example: *Let this be an implication about a triangle ‘T’: - If T is equilateral, then T is isosceles *So the converse would be: - If T is Isosceles, then T is equilateral - Note that the implication (If-Then) is true in this case, but the converse is not.

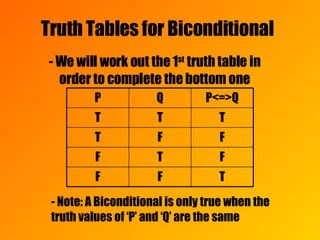
20. Biconditional A biconditional of statements P and Q is denoted P<=>Q and is read “P if and only if Q” A biconditional is nothing more than an “if-then” statement joined with its converse by an “And” – [(P=>Q)^(Q=>P)] Note: the prefix “bi” means 2, so biconditional means “2 conditionals (If-Then)’

21. Truth Tables for Biconditional - We will work out the 1 st truth table in order to complete the bottom one - Note: A Biconditional is only true when the truth values of ‘P’ and ‘Q’ are the same T F F F T F F F T T T T P<=>Q Q P