This document contains notes from a lecture on Boolean logic. It introduces concepts like negation, conjunction, disjunction and provides examples of how to represent them symbolically. Negation rules are discussed, as well as conjunction and disjunction rules. Truth tables are presented as a way to determine if a formula is a tautology or logical consequence. The document also discusses logical equivalence and normalization of formulas by pushing negations inward.

1. Truth, Deduction,
Computation
Lecture 5
Boolean Logic
Vlad Patryshev
SCU
2013

2. Earlier we had…
<atomic formula> ::= <predicate>(<arguments>)
<arguments> ::= <term>|<arguments>,<term>
Now let’s build formulas
out of atomic formulas!

3. (Chapter 3)
Negation
●
●
●
●
●
not(a)
!a
~a
a
¬a
P
¬P
TRUE
FALSE
FALSE TRUE
Notation:
a ≠ b means ¬(a = b)
¬¬¬Cube(c) is the same as ¬Cube(c)
¬¬Cube(c) is the same as Cube(c)?

4. Negation
●
●
●
●
●
not(a)
!a
~a
a
¬a
Notation:
a ≠ b means ¬(a = b)
P
¬P
TRUE
FALSE
FALSE TRUE
Well...
¬¬¬Cube(c) is the same as ¬Cube(c)
¬¬Cube(c) is the same as Cube(c)? ...it depends...

5. Negation Rules
●
If P is a sentence, so is ¬P
●
A sentence that is either atomic
or a negation of atomic is called
literal

6. Conjunction
●
●
●
●
a
a
a
a
and b
∧ b
& b
&& b
Q
P∧Q
TRUE
TRUE
TRUE
TRUE
FALSE
FALSE
FALSE
Examples:
P
TRUE
FALSE
FALSE
FALSE
FALSE
● Tet(f) ∧ Small(f)
● ¬(Tet(f) ∧ ¬Large(f)
● if (1 < a && a < 1) alert(“ouch”)
Well...

7. Disjunction
●
●
●
●
a
a
a
a
or b
v b
| b
|| b
Q
PvQ
TRUE
TRUE
TRUE
TRUE
FALSE
TRUE
FALSE
Examples:
P
TRUE
TRUE
FALSE
FALSE
TRUE
● Tet(f) v Small(f)
● ¬(Tet(f) v ¬Large(f)
● if (0 < a || a < 0) alert(“good”)
● Dead(AshwathamaTheHuman) or Dead(AshwathamaTheElephant)
Well...

8. Conjunction and Disjunction Rules
●
If P and Q are sentences, so is P∧Q
●
If P and Q are sentences, so is PvQ

9. Need Parentheses
● Home(max) v Home(claire) ∧ Happy(carl)
● ¬ Home(max) v ¬ Home(claire) ∧ Happy(carl)
Avoid Ambiguity
(remember Yudhisthira)

10. Associativity Rules (or are they laws?)
● ((P ∧ Q) ∧ R) <=> (P ∧ (Q ∧ R))
● ((P v Q) v R) <=> (P v (Q v R))
Actually… we have two monoids!

11. Commutativity Rules
● P ∧ Q <=> Q ∧ P
● P v Q <=> Q v P
We have two commutative monoids!

12. Idempotence Rules
● P ∧ P <=> P
● P v P <=> P
We have two commutative idempotent monoids!
(we are closer to sets than we thought)

13. Logical Formulas, formally
<formula>
<formula>
<formula>
<formula>
<formula>
::=
::=
::=
::=
::=
<atomic formula>
¬<formula>
(<formula>)
<formula>v<formula>
<formula>∧<formula>

14. Some More Laws
● Double Negation: ¬¬P ⇔ P
● DeMorgan: ¬(P ∧ Q) ⇔ ¬P v ¬Q
● DeMorgan: ¬(P v Q) ⇔ ¬P ∧ ¬Q

15. (Chapter 4)
Philosophy on Page 94
“it is necessarily the case that S” - what’s the
difference with just S?
If a formula depends on entities, it’s called
“Truth-functional”
And if it is always (constant) true, it can be
considered as “not truth-functional”... see next

16. More definitions
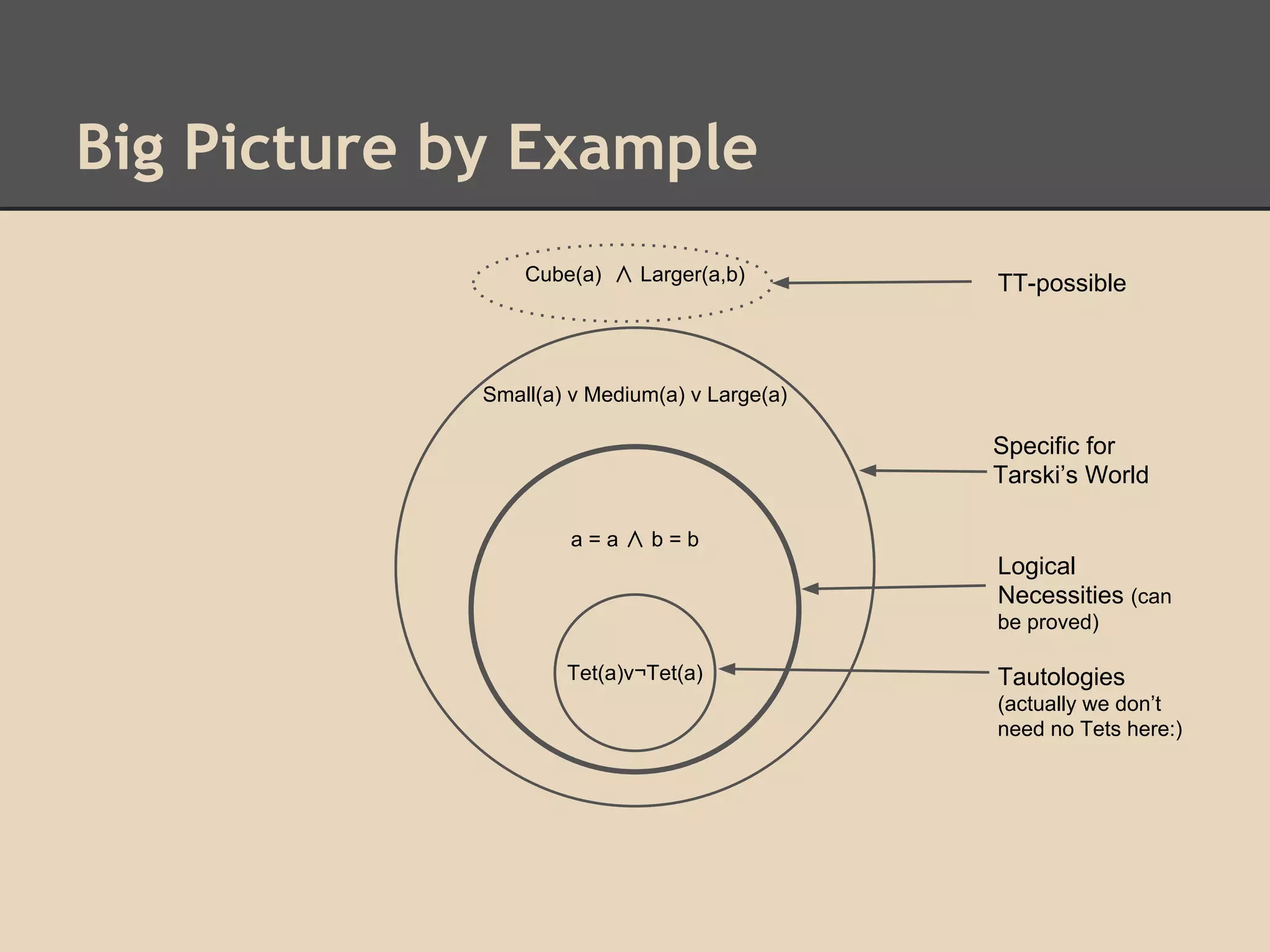
Logical Truth - “logically necessary sentences” consequences that follow from an empty list of premises
Logical Possibility - “logically possible sentences” sentences which negation cannot be proven for a given
collection of entities and rules
(example in Tarsky World)
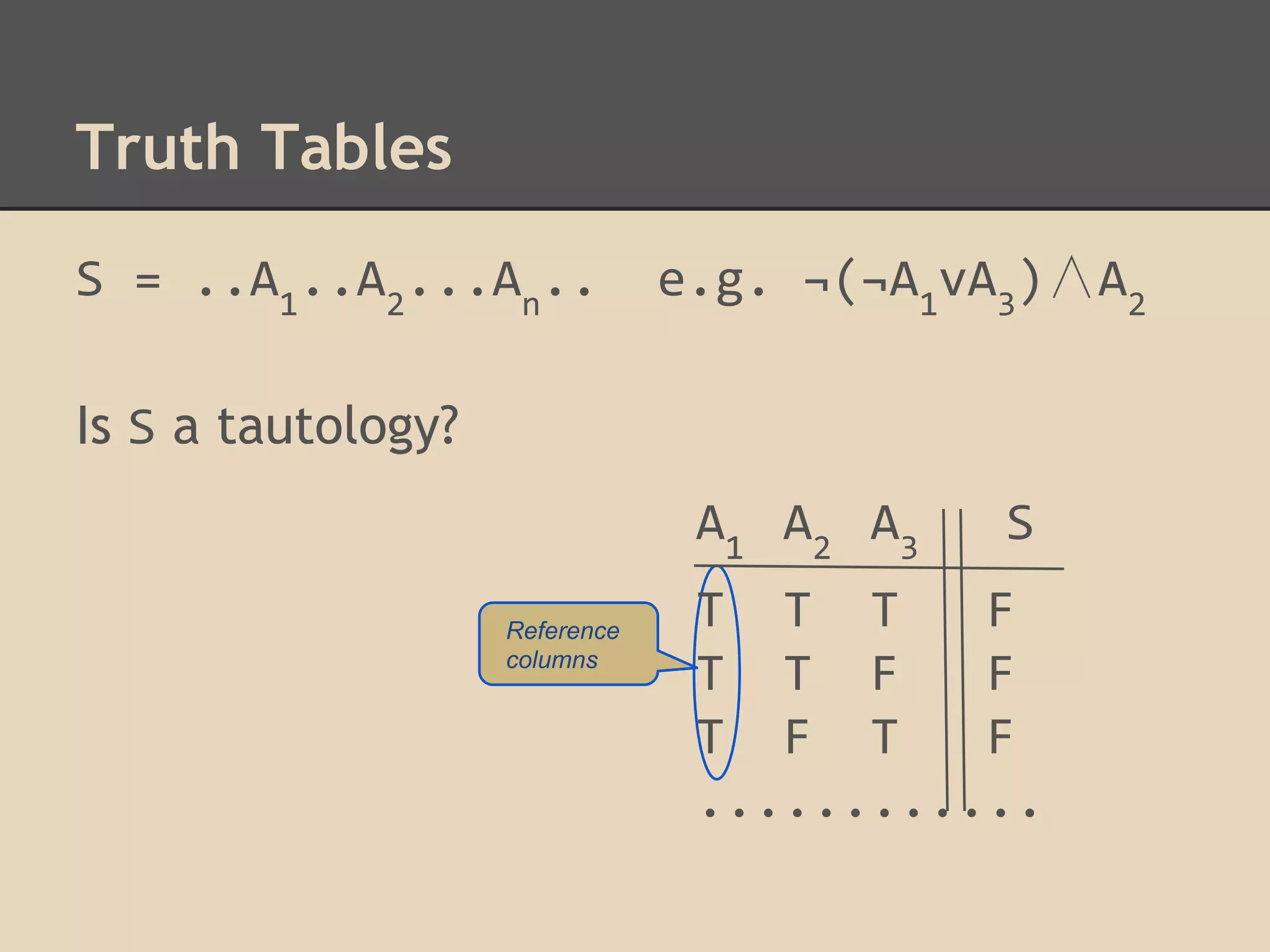
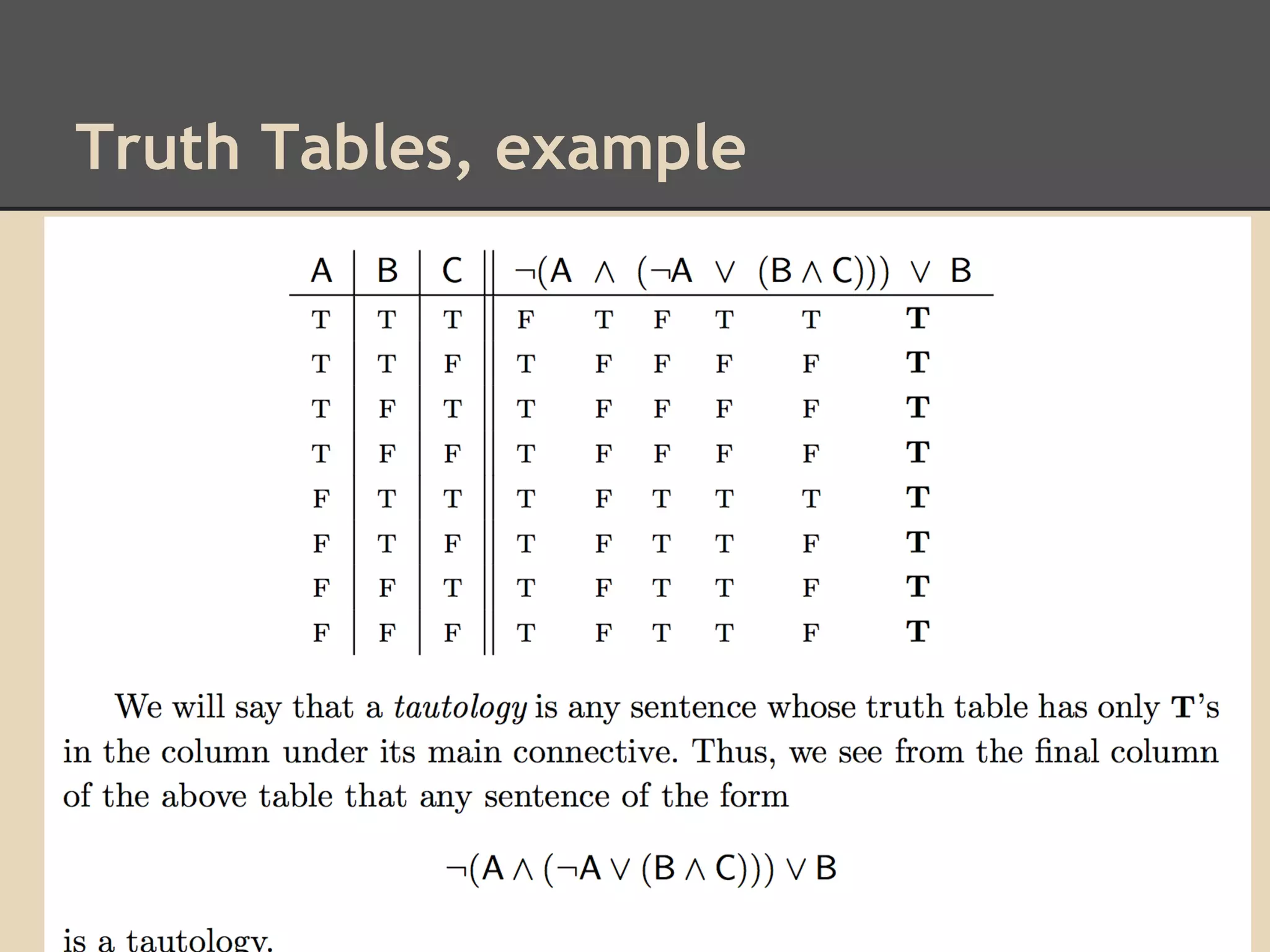
Tautology (from Greek ταυτολογία) is a formula which is
true in every possible interpretation. [wikipedia] That is, it
will be true, whatever the argument entities.

17. Truth Tables
S = ..A1..A2...An..
e.g. ¬(¬A1vA3)∧A2
Is S a tautology?
A1 A2 A3
Reference
columns
S
T T T
F
T T F
F
T F T
F
............

18. Truth Tables, example

19. Big Picture by Example
Cube(a) ∧ Larger(a,b)
TT-possible
Small(a) v Medium(a) v Large(a)
Specific for
Tarski’s World
a=a∧b=b
Logical
Necessities (can
be proved)
Tet(a)v¬Tet(a)
Tautologies
(actually we don’t
need no Tets here:)

20. Equivalence of sentences
Two sentences are...
Logically equivalent
if each can be deduced from
another.
Tautologically equivalent
if they take the same values
in truth tables.
E.g. a=b and b=a
E.g. ¬(A∧B) and ¬A v ¬B

21. Example from the book
if (!((A || B) && !C) println(“completely satisfied”)
if ((!A && !B) || C) println(“absolutely satisfied”)

22. Consequence of sentences
Remember lecture 5?
A is a logical consequence
A is a tautological consequence
of B if we can build a proof of B if in the truth table every
time B is true, A is true.
E.g. a=b∧с=b yields c=a
E.g. A∧B yields AvB

23. Try 4.24

24. Try 4.24
Never mind, FITCH has Taut Con

25. Remember the Laws?
● Double Negation: ¬¬P ⇔ P
● DeMorgan: ¬(P ∧ Q) ⇔ ¬P v ¬Q
● DeMorgan: ¬(P v Q) ⇔ ¬P ∧ ¬Q

26. Pushing Negation Around
Will use the laws
E.g.
¬(Cube(a) ∧ ¬¬Small(a))
¬(Cube(a) ∧ Small(a))
¬Cube(a) v ¬Small(a)
Hmm… wait… who said it is legal?!...

27. We use Substitution!
P ⇔ Q
S(P) - contains P somewhere inside
then
S(P) ⇔ S(Q)
Kind of obvious for tautological equivalence, but…
We’ll get back to it later

28. Normalization. Step 1. Negation
NNF, Negation Normal Form
all negations by atomic formulas. (remember
“literal”?)
E.g.
¬¬¬(¬A v ¬(B∧C) v D) ⇔
¬(¬A v ¬(B∧C) v D)
⇔
A ∧ (B∧C) ∧ ¬D)

29. Remember, we have...
● associativity
● commutativity
● idempotence
Together with de Morgan laws, they do miracles
We can simplify expressions.

30. Simplifying Logical Sentence
(A v B) ∧ C ∧ (¬(¬B ∧ ¬A) v B) ⇔
(A v B) ∧ C ∧ ((¬¬B v ¬¬A) v B) ⇔
(A v B) ∧ C ∧ ((B v A) v B) ⇔
(A v B) ∧ C ∧ (B v A v B) ⇔
(A v B) ∧ C ∧ (A v B v B) ⇔
(A v B) ∧ C ∧ (A v B) ⇔
(A v B) ∧ (A v B) ∧ C ⇔
(A v B) ∧ C

31. That’s it for today