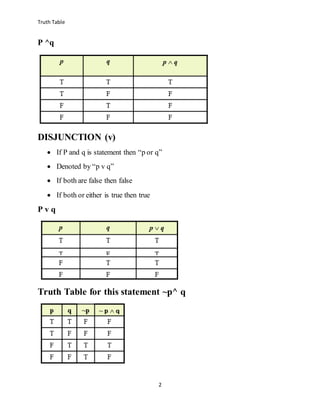
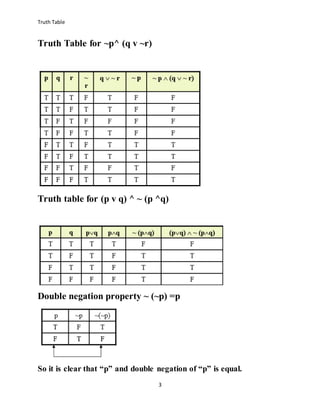
A truth table specifies the truth values of a compound proposition for all possible truth values of its constituent propositions. It is a convenient method for analyzing compound statements. A truth table shows the truth values of statements involving logical connectives such as negation, conjunction, and disjunction. De Morgan's laws state that the negation of a conjunction is the disjunction of the negations, and the negation of a disjunction is the conjunction of the negations. Truth tables can be used to show that expressions following from De Morgan's laws are logically equivalent.

1. Truth Table
1
WHAT IS TRUTH TABLE
A truth table specifies the truth value of a compound proposition for all possible
truth values of its constituent proposition.
A convenient method for analyzing a compound statement is to make a truth table
to it
NEGATION (~)
 If p=statement variable, then negation of ‘p’ “NOT p”, is denoted by “~p”
 If p is true, ~p is false
 If p is false ~p is true
TRUTH TABLE FOR ~P
CONJUNCTION (^)
 If p and q is statement then conjunction is “p and q”
 Denoted by “p ^q”
 If p and q are true then true
 If both or either false then False

2. Truth Table
2
P ^q
DISJUNCTION (v)
 If P and q is statement then “p or q”
 Denoted by “p v q”
 If both are false then false
 If both or either is true then true
P v q
Truth Table for this statement ~p^ q

3. Truth Table
3
Truth Table for ~p^ (q v ~r)
Truth table for (p v q) ^ ~ (p ^q)
Double negation property ~ (~p) =p
So it is clear that “p” and double negation of “p” is equal.

4. Truth Table
4
Example
English to symbolic
P= I am Ali
~p= I am not Ali
~ (~p) = I am Ali
So it is clear that double negation of “p”is also equal to “p”.
~ (p ^q) & ~p ^~q are not logically Equivalent.
So it is clear that “~ (p ^q) & ~p ^~q” are not equal
De Morgan’s Law
1. The negation of “AND” statement is logically equivalent to the “OR”statement
in which each component is negated.
Symbolically ~ (p ^q) = ~p v ~q
P q P ^q ~(p ^q) ~p ~q ~p v ~q
T T T F F F F
T F F T F T T
F T F T T F T
F F F T T T T
So it is clear that ~ (p ^q) = ~p v ~q are logically equivalent

5. Truth Table
5
2. The negation of “OR”statement is logically equivalent to the “AND” statement
in which componentis negated.
Symbolically ~ (p v q) = ~p ^ ~q
So it is clear that ~ (p v q) = ~p ^ ~q is Equal.
Application
Negation for each of the following:
a. The fan is slow ‘OR’ it is very hot
b. Ali is fit ‘OR’ Akram is injured.
Solution:
a. The fan is not slow “AND” it is not very hot
b. Ali is not fit “AND” Akram is not injured

6. Truth Table
6
Inequalities and Demorganes laws
1. (p ^q) ^ r = P^(q ^ r)
p q r (p ^q) (q ^r) (p ^q)^r P^(q ^r)
T T T T T T T
T T F T F F F
T F T F F F F
T F F F F F F
F T T F T F F
F T F F F F F
F F T F F F F
F F F F F F F
So it clears that Colum 6 and Colum 7 are equal
2. (P ^q) v r = p ^ (q v r)?????
P q r (p ^q) (q v r) (p ^q) v r P ^(q v r)
T T T T T T T
T T F T T T T
T F T F T T T
T F F F F F F
F T T F T T F
F T F F T F F
F F T F T T F
F F F F F F F
So it clear that Colum 6 and Colum 7 are not equal.