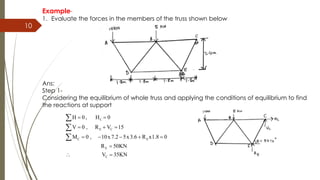
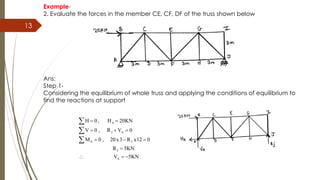
1) A truss is a structure composed of straight members connected at joints that allows the members to only experience axial forces from the connections and any applied loads. 2) Trusses are divided into bridge trusses and roof trusses with various types of each including Pratt, Howe, Warren, and more. 3) Trusses can be analyzed through the method of joints which involves applying equilibrium conditions to each joint sequentially or the method of sections which uses equilibrium on a cut portion of the truss to directly find member forces.

1. Truss
Presented By,
Miss. Shinde Bharti M. (Assistant Professor)
Department of Civil Engineering
Sanjivani College of Engineering, Kopargaon.
Email- shindebharticivil@sanjivani.org.in
1

2. Definition of Truss-
A truss is a structure comprising one or more triangular
units constructed with straight members where ends are
connected at its joints or nodes.
A truss is held in position by supports and loads are applied at
joints only
The free body diagram of a member shows that it is acted upon
by two equal and opposite forces.
The hinged/pinned joint permits the members to rotate with
respect to each other and hence members are subjected to
purely axial forces i.e. tension or compression
2

3. 3
Types of Trusses-
Trusses are mainly divided into two parts as,
1. Bridge Truss
• Pratt Bridge Truss
• Howe Bridge Truss
• Baltimore Bridge Truss
• K-Bridge Truss
• Warren Bridge Truss
• Bailey Bridge Truss
2. Roof Truss
• Pratt Roof Truss
• Fink Roof Truss
• Howe Roof Truss
• Warren Roof Truss
• King Post Roof

4. 4
Analysis of Trusses-
Statical Determinancy-

5. 5
Truss can also be classified into three types based on statical
indeterminacy
1. Perfect Truss- m=2j-3
2. Deficient Truss- m<2j-3
3. Reduntant Truss- m>2j-3

6. 6
Continued…….
 Assumptions-



 Methods Of Analysis-



7. 7
Method of Joints-
The procedure for analysis of truss using method of joint is,
1. Obtain the support reactions first considering the conditions of equilibrium,
applied to truss as a hole ( )
2. Then, take the free body diagram of a joint (preferably) which has not more
than two unknowns and applying the conditions of equilibrium for a
concurrent force system as ( ) the unknowns are determined.
3. The analysis is continued with the equilibrium of next joint until the forces in all
the members are evaluated.
H 0, V 0, M 0    
H 0, V 0  

8. 8
Zero force Members-
For simplification of analysis one can identify the zero force members as,
1. When two of the three members meeting at a joint are collinear, and no external
load is acting at the joint then the force in the third member is zero.
2. When two members meet at a joint where no load is acting , then the forces in
those members are zero.

9. 9 3. When two members meet at a joint there is support such that the support reaction is
collinear with any one member, then the force in the other member is zero.

10. 10
Example-
1. Evaluate the forces in the members of the truss shown below
Ans:
Step 1-
Considering the equilibrium of whole truss and applying the conditions of equilibrium to find
the reactions at support
C
E C
C E
E
C
H 0 , H 0
V 0 , R V 15
M 0 , 10x7.2 5x3.6 R x1.8 0
R 50KN
V 35KN
 
  
    

 




11. 11
Step2-
Consider a joint one by one as concurrent force system, and apply conditions of
equilibrium to evaluate the unknowns.
Joint C
Joint E
Joint B
Joint D
BC CE
CE
CE BC
H 0 , F F (cos53.13) 0
V 0 , F (sin53.13) 35
F 43.75KN (C) and F 26.25KN (T)
   
  
  


CE BE DE
CE BE
BE DE
H 0 , F (cos53.13) F (cos53.13) F 0
V 0 , F (sin53.13) F (sin53.13) 50 0
F 18.75KN (C) and F 15KN (T)
   
   
  


BC AB BD BE
BD BE
BD AB
H 0 , F F F (cos53.13) F (cos53.13) 0
V 0 , 5 F (sin53.13) F (sin53.13) 0
F 12.5KN (T) and F 7.5KN (T)
    
    
  


BD AD DE
BD AD
AD
H 0 , F (cos53.13) F (cos53.13) F 0
V 0 , F (sin53.13) F (sin53.13) 0
F 12.5KN (C)
   
  
 



12. 12
Method of Sections-
In this method the forces in the members can be determined directly instead of
considering the equilibrium of joints one by one. The procedure for analysis of truss using
method of section is,
1. Obtain the support reactions first considering the conditions of equilibrium, applied to
truss as a hole ( )
2. Then, take the imaginary cutting line through the truss, dividing it into two parts, such
that it passes through the members and cuts maximum three members in which the
forces are to be determined.
3. Now, consider any one part of the truss left or right side of the section and apply the
conditions of equilibrium for the non-concurrent force system ( )
to evaluate the unknown forces.
H 0, V 0, M 0    
H 0, V 0, M 0    

13. 13
Example-
2. Evaluate the forces in the member CE, CF, DF of the truss shown below
Ans:
Step 1-
Considering the equilibrium of whole truss and applying the conditions of equilibrium to
find the reactions at support
A
J A
A J
J
A
H 0 , H 20KN
V 0 , R V 0
M 0 , 20x3 R x12 0
R 5KN
V 5KN
 
  
  

  




14. 1414
Step2-
Consider an imaginary cut line passing through the members CE, CF, DF , and take left side
of the section as non-concurrent force system, and apply conditions of equilibrium to
evaluate the unknowns.
CE CE CF DF A
A CF
C A DE
CE CF DE
H 0 , 20 F F F (cos45) F H 0
V 0 , V F (sin 45) 35
M 0 , 20x3 V x3 F x3 0
F 10KN (T), F 7.071KN(C) and F 15KN (T)
       
  
   
   




15. 15

16. 16
Thank You