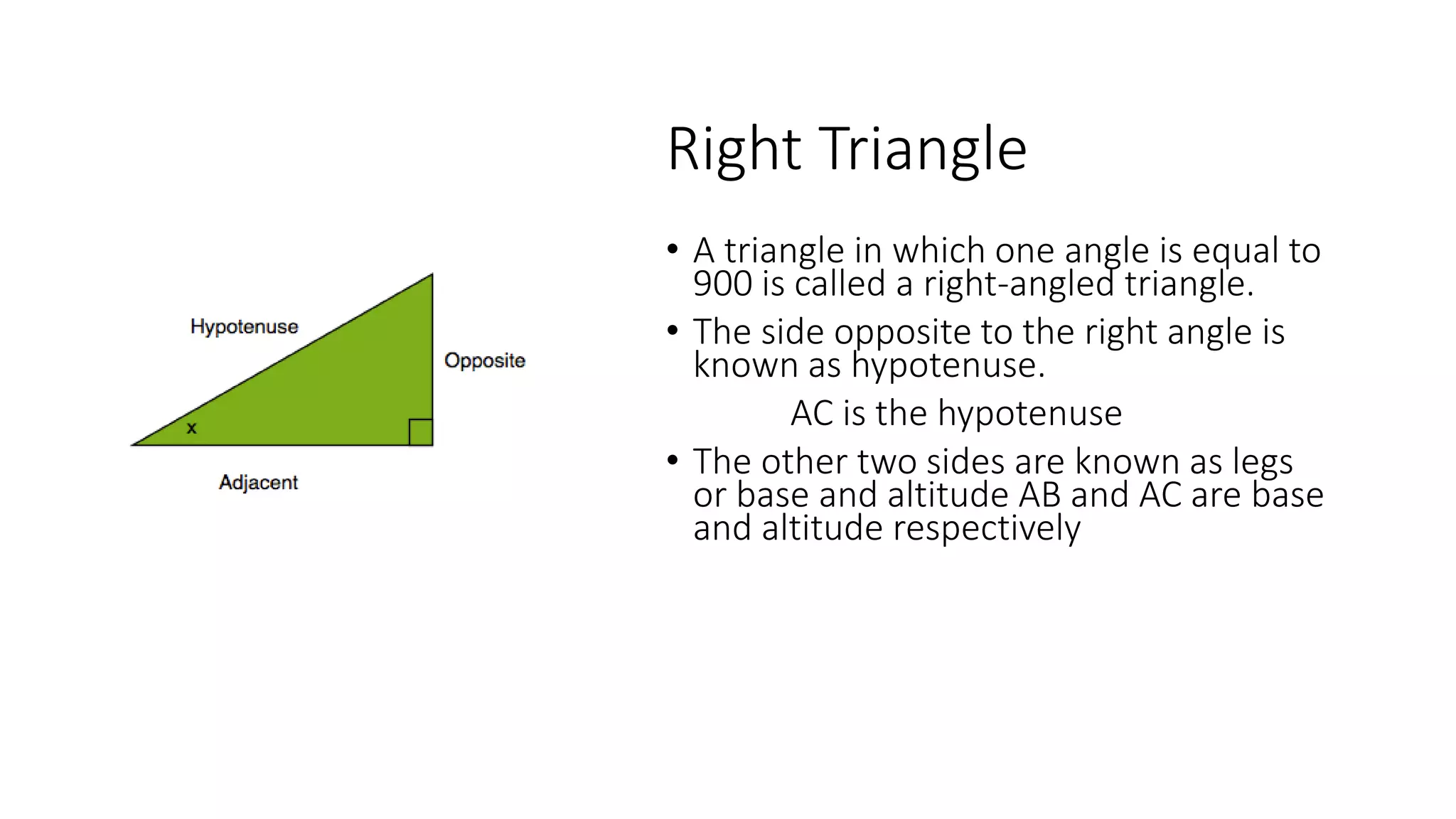
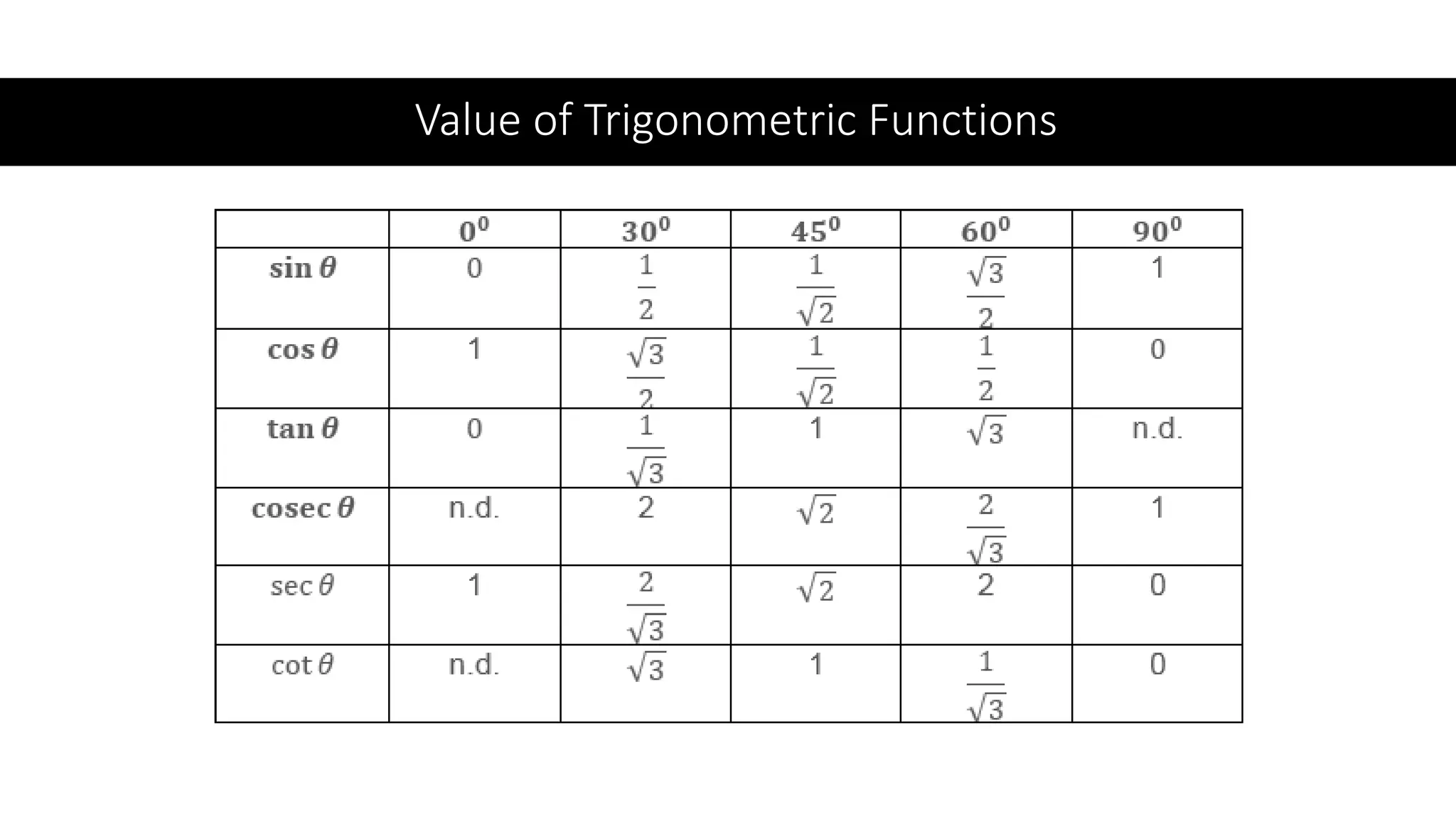
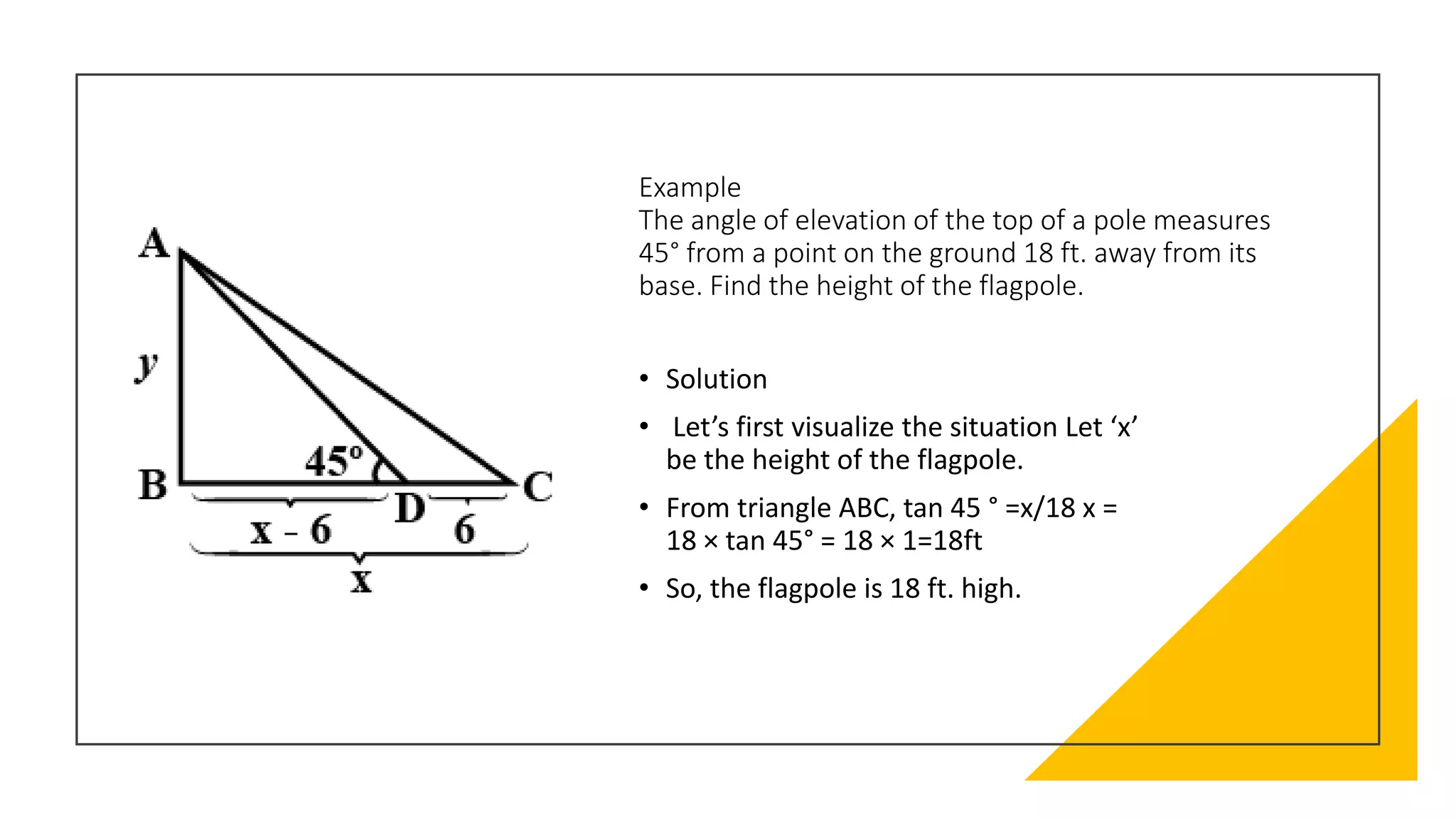
This document provides an introduction to trigonometry, including its history and key concepts. Trigonometry deals with right triangles and relationships between their sides. Important concepts discussed include the trigonometric ratios (sine, cosine, tangent etc.), Pythagorean theorem, and applications to fields like construction, astronomy, and engineering. An example problem demonstrates using trigonometric functions to calculate the height of a flagpole given the angle of elevation and distance from the base.

1. APPLICATION
OF
TRIGONOMETRY

2. INTRODUCTION
• Trigonometry is the branch of mathematics that deals
with triangles particularly right triangles.
• They are behind how sound and light move and are
also involved in our perceptions of beauty and other
facets on how our mind works.
• So trigonometry turns out to be the fundamental to
pretty much everything!

3. History
• The origins of trigonometry can be traced to the
civilizations of ancient Egypt, Mesopotamia and the
Indus Valley, more than 4000 years ago
• Some experts believe that trigonometry was originally
invented to calculate sundials
• The first recorded use of trigonometry came from the
Hellinistic mathematician Circa in 150 BC.
• Many mathemiticians like Aryabhatta, Ibn Yunus and
Al-Kashi also contributed significantly.

4. Right Triangle
• A triangle in which one angle is equal to
900 is called a right-angled triangle.
• The side opposite to the right angle is
known as hypotenuse.
AC is the hypotenuse
• The other two sides are known as legs
or base and altitude AB and AC are base
and altitude respectively

5. Pythagoras Theorem
• In any right triangle, the area of the square whose side is
the hypotenuse is equal to the sum of the areas of the
squares whose sides are the two legs.
• If AB, BC, and AC are the sides of the triangle, then: BC2 =
AB2 + AC2​. While if a, b, and c are the sides of the triangle,
then ​c2 = a2 + b2

6. Trigonometric Ratios
• Sine (sin)  Opposite side / Hypotenuse
• Cosine (cos)  Adjacent side / Hypotenuse
• Tangent (tan)  Opposite side / Adjacent side
• Cosecant (cosec)  Hypotenuse / Opposite side
• Secant (sec)  Hypotenuse / Adjacent side
• Cotangent (cot)  Adjacent side / Opposite side

7. Value for Trigonometric Functions for Angle C
• Sinθ = AB/AC
• Cosθ = BC/AC
• Tanθ = AB/BC
• Cosecθ = AC/AB
• Secθ = AC/BC
• Cotθ = AC/AB
C
A
B
Adjacent
Opposite

8. Value of Trigonometric Functions

9. Some Applications of
Trigonometry
• Main use is in Construction or else this
field of mathematics can be applied in
astronomy,navigation, acoustics
medical imaging, civil engineering,
seismology, electrical engineering
phonetics, chemistry, number theory
and many more.

10. Example
The angle of elevation of the top of a pole measures
45° from a point on the ground 18 ft. away from its
base. Find the height of the flagpole.
• Solution
• Let’s first visualize the situation Let ‘x’
be the height of the flagpole.
• From triangle ABC, tan 45 ° =x/18 x =
18 × tan 45° = 18 × 1=18ft
• So, the flagpole is 18 ft. high.

11. Conclusion
• Trigonometry is a branch of
Mathematics with several
important and useful applications.
Hence, it attracts more and more
research with several theories
published year after year.

12. Thank you!
Done by Aksar Ali 😊