1. A triangle is a closed figure formed by three intersecting lines, with three sides, three angles, and three vertices.
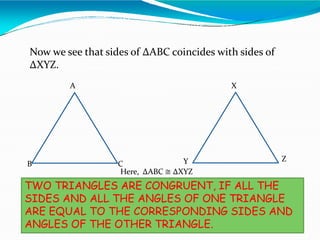
2. There are five criteria to determine if two triangles are congruent: side-angle-side (SAS), angle-side-angle (ASA), angle-angle-side (AAS), side-side-side (SSS), and right-angle-hypotenuse-side (RHS).
3. Key properties of triangles include: angles opposite equal sides are equal; sides opposite equal angles are equal; the sum of any two sides is greater than the third side.