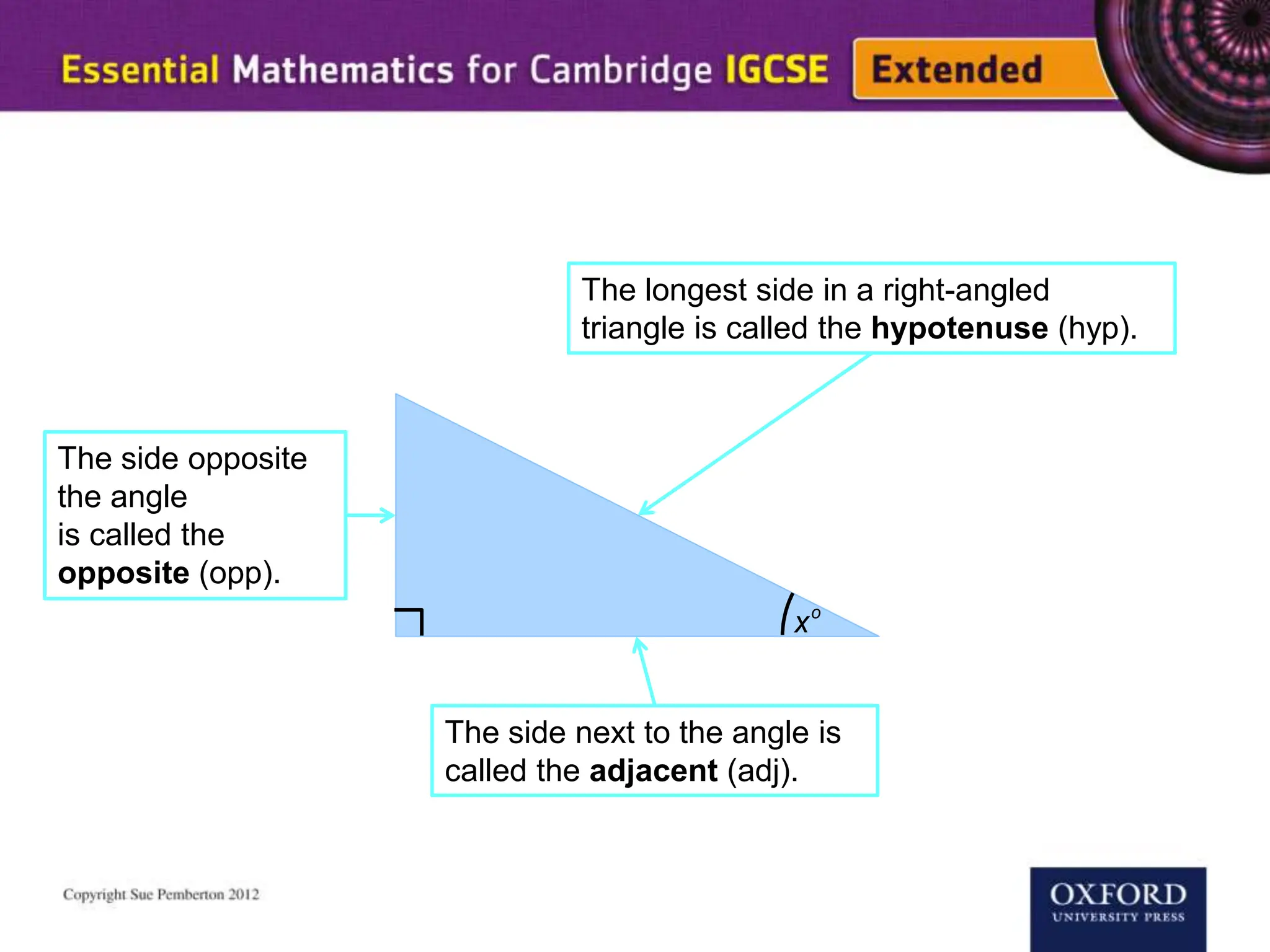
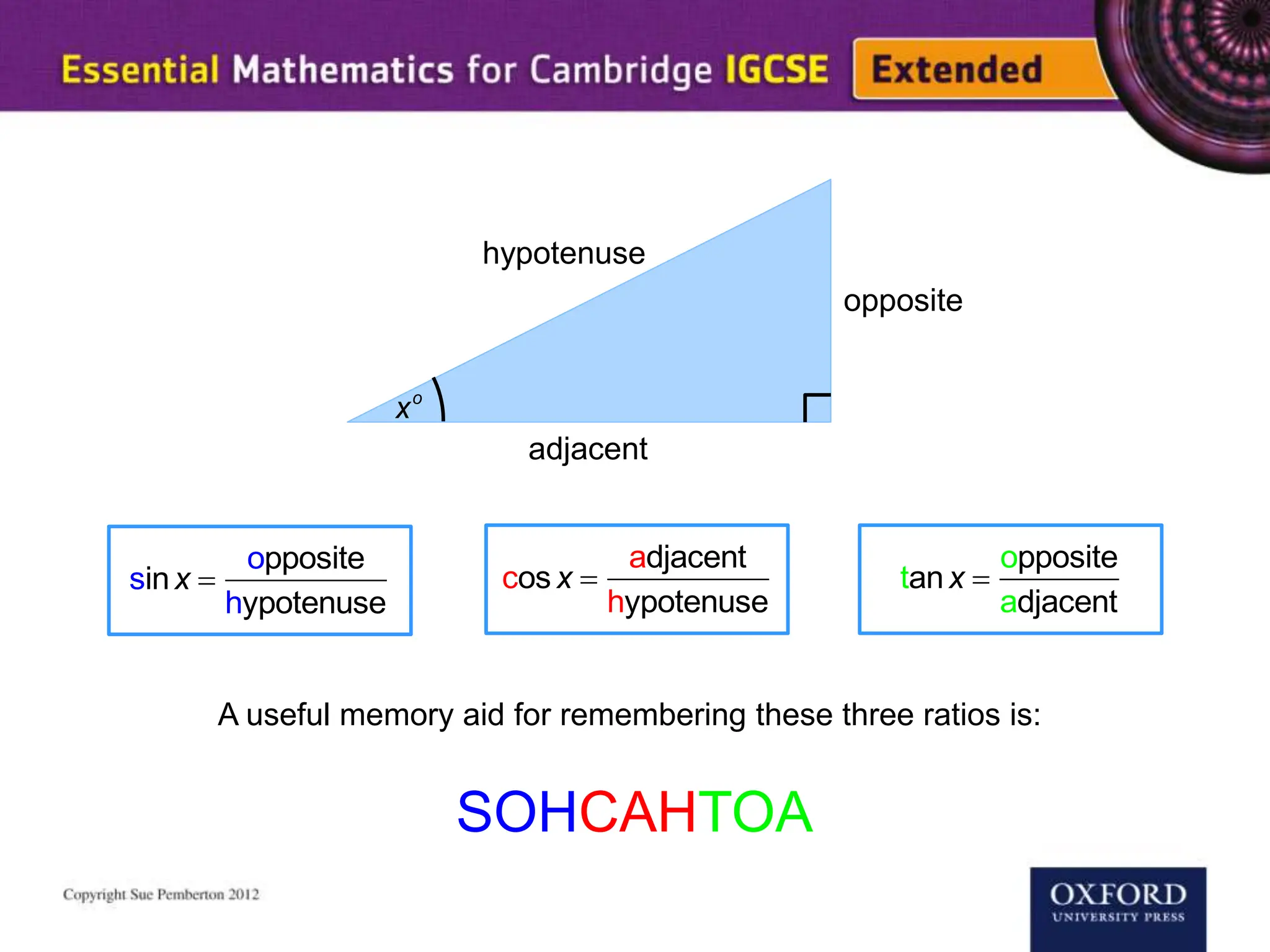
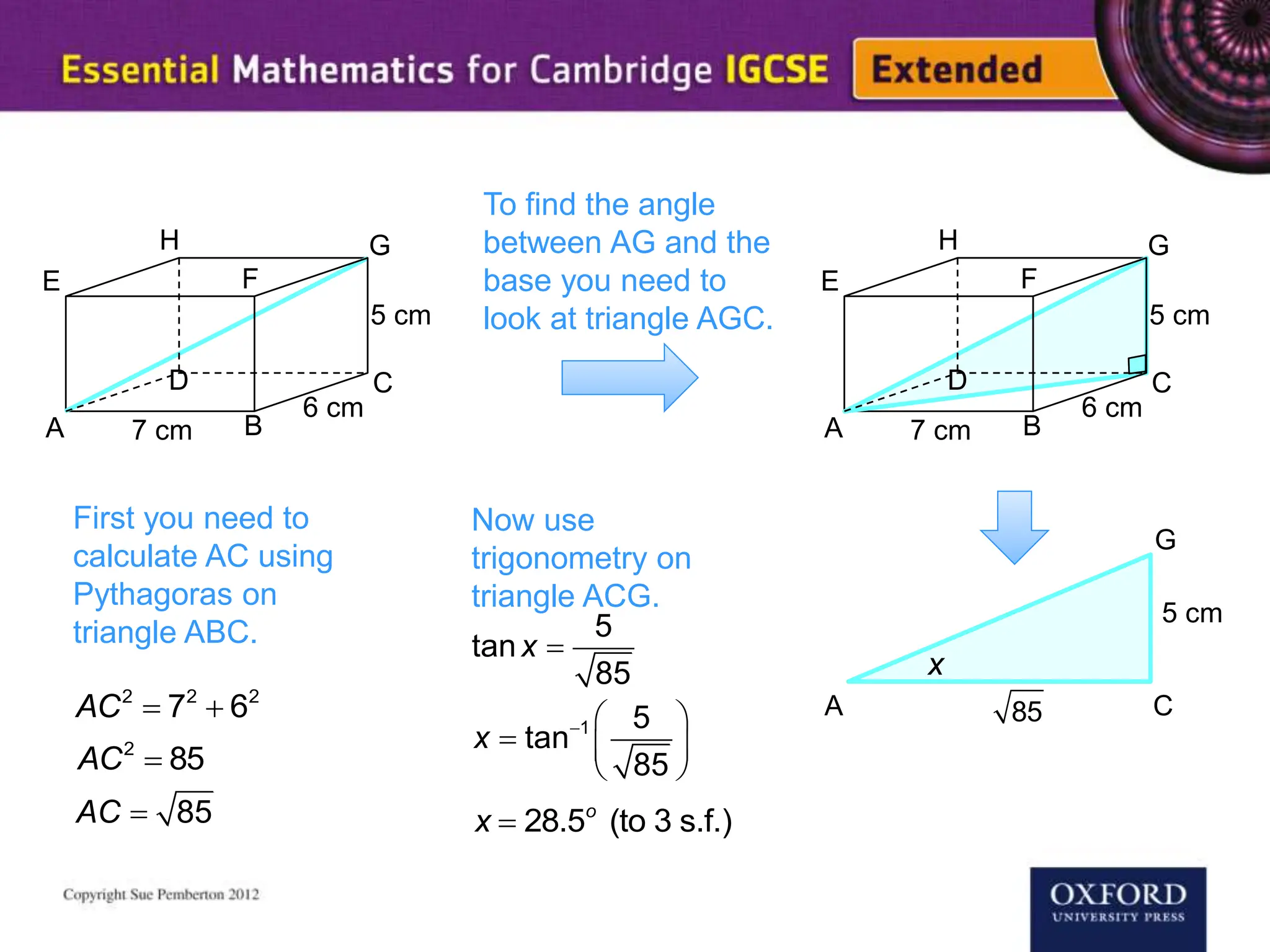
This document explains key concepts of trigonometry, focusing on the definitions of sides in a right-angled triangle: hypotenuse, adjacent, and opposite. It provides examples of calculating the length of sides and angles using trigonometric ratios such as sine, cosine, and tangent. Additionally, it touches on three-dimensional trigonometry with an example involving the calculation of angles and side lengths using Pythagorean theorem and trigonometric functions.

1. Trigonometry

2. The longest side in a right-angled
triangle is called the hypotenuse (hyp).
xo
The side next to the angle is
called the adjacent (adj).
The side opposite
the angle
is called the
opposite (opp).

3. xo
hypotenuse
opposite
adjacent
tanx 
opposite
adjacent
cos x 
adjacent
hypotenuse
sinx 
opposite
hypotenuse
A useful memory aid for remembering these three ratios is:
SOHCAHTOA

4. Finding the length of a side

5. 24o
x
6 cm
Example
1 Find the value of x.
opp
adj
tan24o

opp
adj
tan24o

x
6
x  6  tan24o
x  2.67 cm (to 3 s.f.)
replace opp by x and adj by 6
multiply both sides by 6

6. 73o
x
8 cm
Example
2 Find the value of x.
adj
hyp
cos73o

adj
hyp
cos73o

x
8
x  8  cos73o
x  2.34 cm (to 3 s.f.)
replace adj by x and hyp by 8
multiply both sides by 8

7. 40o
x 5 cm
Example
3 Find the value of x.
opp
hyp
sin40o

opp
hyp
sin40o

x
5
x  5  sin40o
x  3.21 cm (to 3 s.f.)
replace opp by x and hyp by 5
multiply both sides by 5

8. 65o
x
15 cm
Example
4 Find the value of x.
adj
hyp
cos65o

adj
hyp
cos65o

15
x
x  cos65o
 15
x  35.5 cm (to 3 s.f.)
replace adj by 15 and hyp by x
multiply both sides by x
x 
15
cos65o
divide both sides by cos 65o

9. Finding an angle

10. xo
5 cm 9 cm
Example
1 Find the value of x.
opp
hyp
sinx 
opp
hyp
sinx 
5
9
  
  
 
1 5
sin
9
x
x  33.7o
(to 3 s.f.)
replace opp by 5 and hyp by 9
to find x use the sin-1 button on your calculator

11. xo
5 cm
8 cm
Example
2 Find the value of x.
adj
hyp
cos x 
adj
hyp
cos x 
5
8
  
  
 
1 5
cos
8
x
x  51.3o
(to 3 s.f.)
replace adj by 5 and hyp by 8
to find x use the cos-1 button on your calculator

12. xo
3 cm
6 cm
Example
3 Find the value of x.
opp
adj
tanx 
opp
adj
tanx 
3
6
  
  
 
1 3
tan
6
x
x  26.6o
(to 3 s.f.)
replace opp by 3 and adj by 6
to find x use the tan-1 button on your calculator

13. Three dimensional
trigonometry

14. To find the angle
between AG and the
base you need to
look at triangle AGC.
A B
7 cm
C
E
G
H
D
F
6 cm
5 cm
A B
7 cm
C
E
G
H
D
F
6 cm
5 cm
First you need to
calculate AC using
Pythagoras on
triangle ABC.
AC2
 72
 62
AC2
 85
 85
AC
85
Now use
trigonometry on
triangle ACG.

5
tan
85
x
  
  
 
1 5
tan
85
x
x  28.5o
(to 3 s.f.)
A C
G
5 cm
x