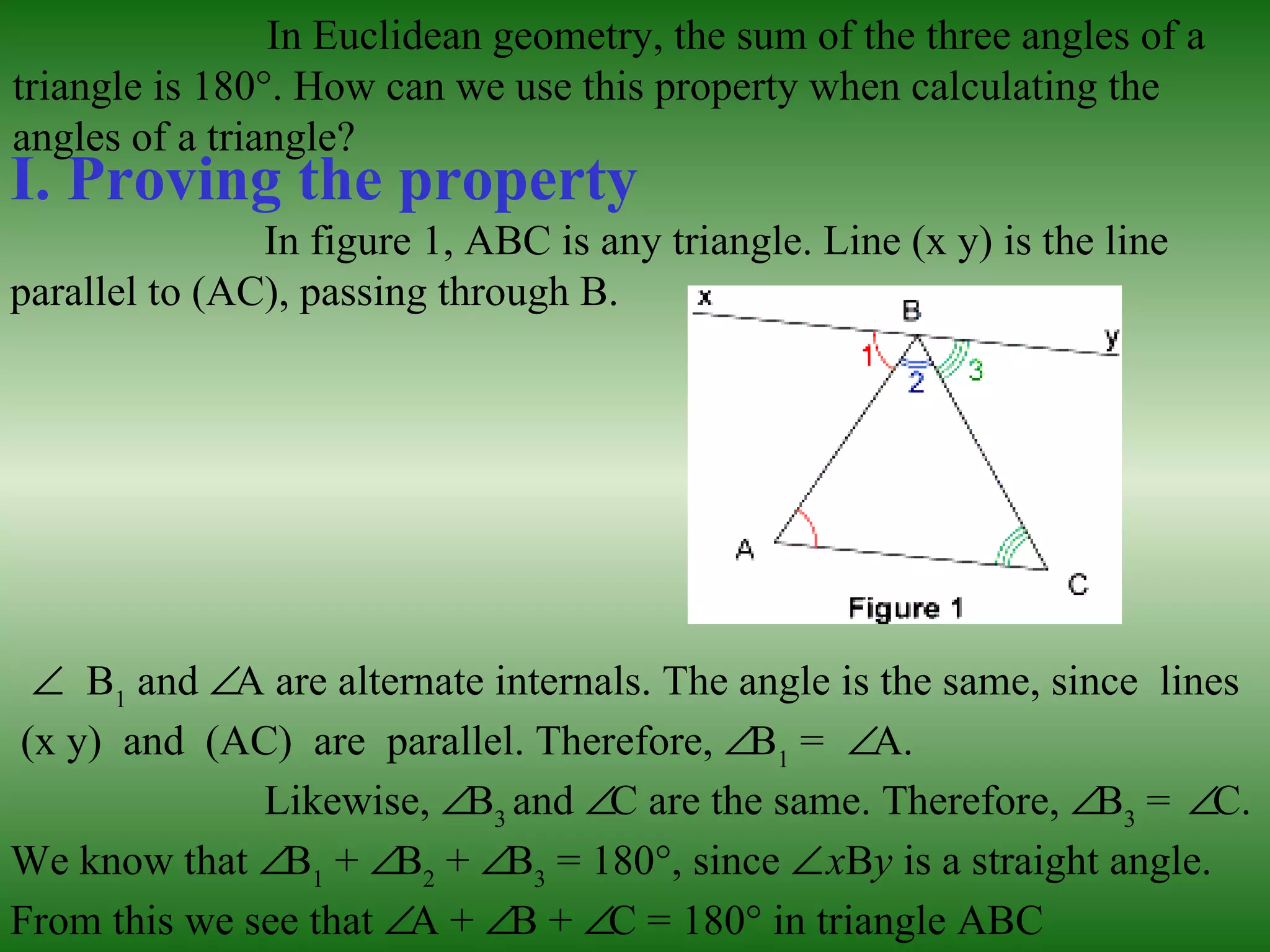
I. The property that the sum of the three angles of any triangle is 180 degrees is proven by drawing a parallel line through one vertex of a triangle. The angles opposite the parallel sides are equal, showing the three angles sum to 180 degrees. II. This property can be used to calculate unknown angles of different types of triangles: A) In a generic triangle, the sum of the three known angles is set equal to 180 degrees to solve for the unknown angle. B) In a right triangle, the two acute angles sum to 90 degrees since one angle is 90 degrees by definition. 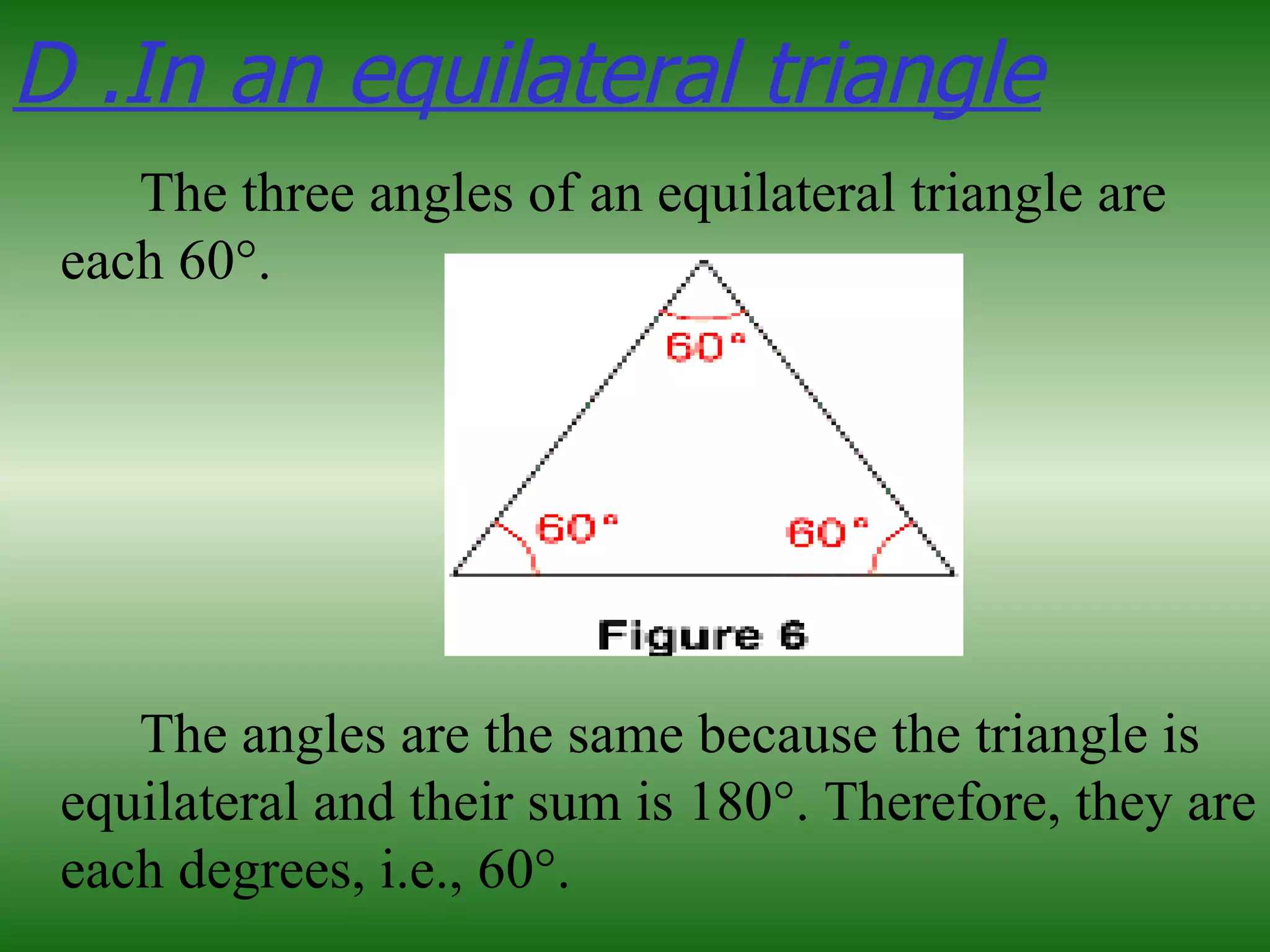C) In an isosceles triangle, the two angles opposite the equal sides are set equal,

1. Name – Ashwani Kumar

2. In Euclidean geometry, the sum of the three angles of a
triangle is 180°. How can we use this property when calculating the
angles of a triangle?
I. Proving the property
In figure 1, ABC is any triangle. Line (x y) is the line
parallel to (AC), passing through B.
∠ B1 and ∠A are alternate internals. The angle is the same, since lines
(x y) and (AC) are parallel. Therefore, ∠B1 = ∠A.
Likewise, ∠B3 and ∠C are the same. Therefore, ∠B3 = ∠C.
We know that ∠B1 + ∠B2 + ∠B3 = 180°, since ∠ xBy is a straight angle.
From this we see that ∠A + ∠B + ∠C = 180° in triangle ABC

3. II. Calculating the angles
A. In any triangle
Example: We want to calculate ∠A of triangle ABC.
We apply the rule ∠A + 114° + 25° = 180°.From this,
we have the calculations: ∠A + 139° = 180° and
∠A = 180° - 139° = 41°.

4. B. In a right-angled triangle
The sum of the two acute angles in a right-angled triangle is 90°.
Triangle ABC has a right angle at A.
So: ∠A = 90°. Therefore, 90° + ∠B + ∠C = 180°, which means ∠B +
∠C = 90°.
Example: We want to calculate ∠B of triangle ABC, shown in
figure 3, which has a right angle at A.
We apply the rule stated previously: ∠B + ∠C = 90°. From this, ∠B +
57° = 90° and ∠B = 90° - 57° = 33°.
∠B is 33°.

5. C. In an isosceles triangle
Example: We want to calculate ∠A and ∠B of isosceles
triangle ABC.
We apply the rule ∠A + ∠B + 48° = 180°. As ABC is an
isosceles triangle in C, we know that ∠A = ∠B;
therefore ∠A + ∠A + 48° = 180°, 2∠A + 48° = 180°,
2∠A = 180°– 48° = 132°, and ∠A (and ∠B ) is 66°.

6. D .In an equilateral triangle
The three angles of an equilateral triangle are
each 60°.
The angles are the same because the triangle is
equilateral and their sum is 180°. Therefore, they are
each degrees, i.e., 60°.