Little Red Riding Hood needs to walk 5 miles to get to her destination. The document shows the time it would take her to walk 5 miles at different speeds: 5 hours if walking at 1 mile per hour, 1 hour if walking at 5 miles per hour, and 0.5 hours or 30 minutes if running at 10 miles per hour. The algebra expression that calculates time for any speed is 5 divided by the speed (5/S). Word problems are translated into algebra expressions so they can be solved mathematically. Examples of key words that translate into different algebra operations are provided.

1. It depends how fast she walks : Time = d / s
Image Source: http://camsp.net

2. Word Problems need to be turned into Algebra Expressions so that
we can do mathematics on them, and work out number answers.
(Or write a Computer App that gets the answer).
Little Red Riding Hood has to walk 5 miles.
If she hops on 1 leg at 1 mile per hour, it will take her 5 hours.
If she walks at 5 miles per hour it will take her 1 hour.
If she runs at 10 miles per hour, it will take her half an hour.
The Algebra Expression that gets the time for any speed she
travels at is : 5 divided by Speed or the “expression” 5 / S .

3. An Algebra Expression is made up of Numbers and
Letters (or “Pronumerals”) as well as + - x symbols.
Examples of Algebra Expressions are:
Y+7
2m
4k / 3
3g – 4k
5–L

4. The Algebra Expression for the “Momentum” of a
moving object is mass x velocity or mv
A light object travelling slowly, like a party balloon, will
have low momentum, and will not hurt you if it bumps
into you. (small mass x low speed = small momentum).
However, a fast running
American Football
player, who has body
weight, and considerable
speed, will make the
recipient of his tackle
definitely feel some big
momentum ! Image Source: http://btfl.tripod.com

5. Algebra Expressions are used to make descriptions of
mathematical situations a lot shorter.
It is much easier to write “mv”, than “mass x velocity”
Think of it like this:
On a Calculator it would take a long time to type in words:
“Six times twelve divided by three equals”
and it is much easier to type in: 6 x 12 2=

6. To translate word problems into Algebra Expressions,
containing letters and numbers, we need to know how to
translate the key words in the problem into mathematical
symbols.
Consider these examples:
“Two added to Four” becomes 2 + 4
“Four multiplied by V” becomes 4V
The following slides provide some translation rules for the
key words that are found in word problems.

7. Words that translate to Adding
plus added to the sum of
sum more than combined together
and increased by heavier than
total next year the total of
combined longer than older than
still gain bigger than
perimeter together older than

8. Words that translate to Subtract
less subtracted subtracted from
difference less than taken away
removed decreased by lighter than
total last year the difference of
separated shorter than younger than
fewer smaller than shorter than
loss differ by how many more

10. Words that translate to Division
Per quotient split so many ways
out of halved divided by
over ratio fraction
split half into equal parts

11. Words that translate to Multiplication
times multiplied by three times as
of doubled increased by a factor of
product tripled quadrupled
area twice as volume

12. Words that translate to Equals
equals results in to obtain
gives will be has a value of
was makes is the same as
is becomes is equivalent to

13. "the quotient of n and 3" n/3
“four less than x" x–4
"the sum of ten and y" y + 10
“Two less than the total of a number and five"
n + 5 – 2 which simplifies to n + 3
"x multiplied by 22“ 22x

14. “Alex has C chocolates, and D drinks. Miley has four
fewer chocolates than Alex, but twice as many
drinks. Write an expression for Miley’s snacks”.
Replace the words with Numbers and Maths symbols.
Four 4
fewer Chocolates C - 4 (Remember minus Reverses)
Twice 2x
as many Drinks 2xD
Answer: C – 4 + 2 x D C - 4 + 2D

15. “In a fruit bowl there are ‘a’ apples and ‘b’ bananas.
In a paper bag there are 6 apples and 8 bananas.
What is the total number of pieces of fruit?”
Replace the words with Numbers and Maths symbols.
‘a’ apples and ‘b’ bananas a+b
6 apples and 8 bananas 6 + 8 ( Not 6a + 8b )
Combining our two expressions we have:
a+b +6+8 Final Answer: a + b + 14

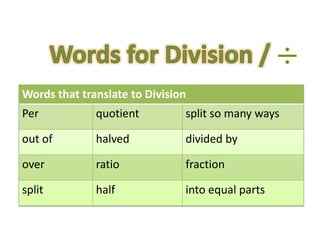
16. “Brad takes ‘h’ hours and ‘m’ minutes to complete a
mini-triathlon. His friend Leonardo takes twice as
long to finish the race. Write an algebra expression
for Leo’s race time.”
‘h’ hours and ‘m’ minutes h+m
Twice ‘h’ hours and ‘m’ minutes 2x h+m
2 x (h + m) 2xh+2xm 2h + 2m [ Not 2h + m ]
Final Answer: 2h + 2m

17. “Johnny has ‘r’ red marbles and ‘b’ blue marbles.
Pete keeps losing his marbles, and has half as many
red marbles, and 5 less blue marbles than Johnny.
Write an expression for Pete’s total marbles”
Half as many red marbles r/2
Five less blue marbles b–5
Source: ipadwallpapers.org
Combining our two expressions we have:
r/2 +b-5 Final Answer: r/2 + b - 5

18. http://passyworldofmathematics.com