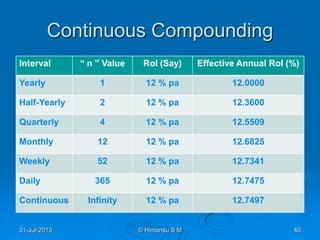
The document presents an overview of interest types, specifically simple and compound interest, along with their calculations. It explains how simple interest is linear and based on principal, time, and rate, while compound interest is exponential and calculated on the accrued principal. Various formulas for calculating both types of interest are provided, along with examples and discussions on compounding frequency and its impact on effective interest rates.











![Comparison [ @ 10% pa ]
Simple Interest
Year Principal Interest
1 100 10
2 100 10
3 100 10
4 100 10
5 100 10
6 100 10
7 100 10
8 100 10
TOTAL 100 80
Compound Interest
Year Principal Interest
1 100 10
2 110 11
3 121 12.1
4 133.1 13.3
5 146.4 14.6
6 161.1 16.1
7 177.2 17.7
8 194.9 19.5
TOTAL 100 114.5
31-Jul-2013 12(C) Himansu S M](https://image.slidesharecdn.com/simpleandcompoundinterest-130801060722-phpapp02/85/Simple-and-Compound-Interest-12-320.jpg)








![Formula for Compound Interest
A = P * ( 1 + i / 100 / n ) ^ ( t * n )
[ the symbol ^ denotes “to the power of” or
“raised to” ]
i = Rate of interest
t = Time period
n = Compounding frequency
P = Principal
A = Amount
31-Jul-2013 21(C) Himansu S M](https://image.slidesharecdn.com/simpleandcompoundinterest-130801060722-phpapp02/85/Simple-and-Compound-Interest-21-320.jpg)


![Formula for Compound Interest
How to find Rate of Interest:
If A, P, t are given
For simplicity let’s assume n=1
Then the formula is:
i = [ { ( A / P ) ^ (1 / t ) } – 1 ] * 100
31-Jul-2013 24(C) Himansu S M](https://image.slidesharecdn.com/simpleandcompoundinterest-130801060722-phpapp02/85/Simple-and-Compound-Interest-24-320.jpg)
![Formula for Compound Interest
Example: Let’s take the Last example
A = 214.4
P = 100
t = 8
n = 1
i = [{( 214.4 / 100 ) ^ ( 1 / 8 )} – 1 ] * 100
= ( 2.144 ^ 0.125 – 1 ) * 100
= ( 1.10 -1 ) * 100 = 0.10 * 100 = 10 % pa
31-Jul-2013 25(C) Himansu S M](https://image.slidesharecdn.com/simpleandcompoundinterest-130801060722-phpapp02/85/Simple-and-Compound-Interest-25-320.jpg)