This document provides instructions on how to sketch parabolas by identifying their key features:
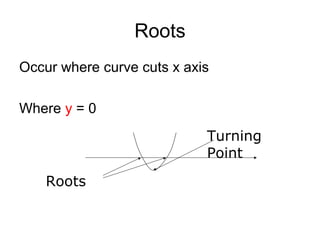
1) Roots occur where the curve cuts the x-axis (where y = 0)
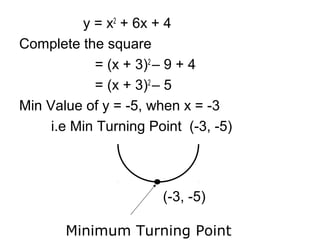
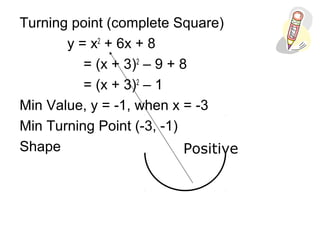
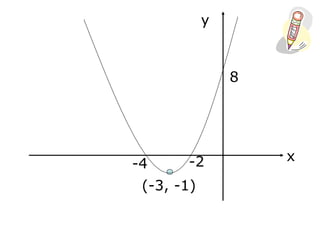
2) Turning points can be found by completing the square of the equation
3) The y-intercept occurs where x = 0
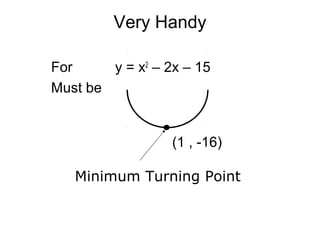
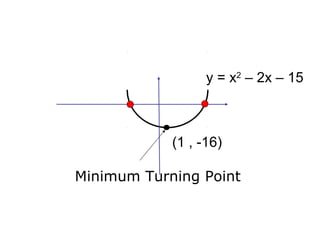
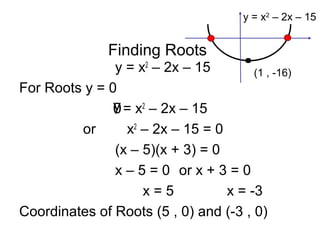
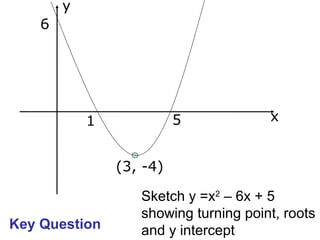
It demonstrates finding these features for equations such as y = x^2 - 2x - 15, identifying the minimum turning point as (1, -16), roots as (5, 0) and (-3, 0), and y-intercept as (0, -15). Finally, it asks the key question of sketching y = x^2 - 6x + 5, showing its