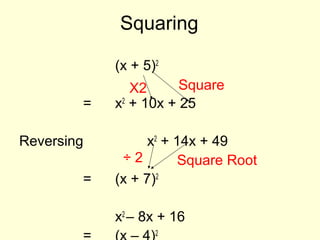
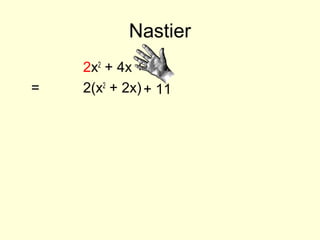
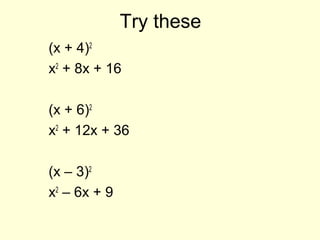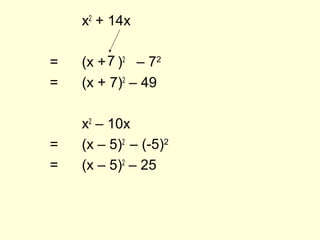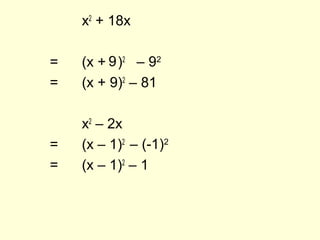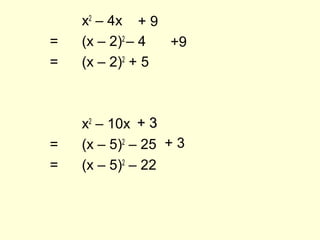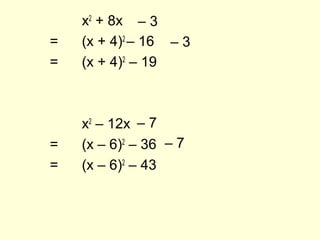1) The document discusses completing the square, which involves rewriting quadratic expressions in the form (x + a)2 + b to find maximum and minimum values. 2) Examples are provided of completing the square for expressions like x2 + 8x + 3 and 2x2 + 4x + 11. 3) The technique of setting the expression equal to 0 and solving for x is described as a way to find the minimum value and the corresponding x-value that produces it.

1. Block 3
Completing the Square

2. What is to be learned?
• How to complete the square
• How to use this to find maximum and
minimum values

3. Try these
(x + 4)2
x2
+ 8x + 16
(x + 6)2
x2
+ 12x + 36
(x – 3)2
x2
– 6x + 9

4. Squaring
(x + 5)2
= x2
+ 10x + 25
Reversing x2
+ 14x + 49
= (x + 7)2
x2
– 8x + 16
2
X2 Square
÷ 2 Square Root

5. x2
+ 6x
x2
+ 6x + 9
= (x + 3)2
Balance by subtracting the square of the
number in brackets!

= – 9
– 9

6. x2
+ 14x
= (x + )2
= (x + 7)2
– 49
x2
– 10x
= (x – 5)2
= (x – 5)2
– 25
7 – 72
– (-5)2

7. x2
+ 18x
= (x + )2
= (x + 9)2
– 81
x2
– 2x
= (x – 1)2
= (x – 1)2
– 1
9 – 92
– (-1)2

8. x2
+ 8x
= (x + 4)2
– 16
= (x + 4)2
+ 1
x2
+ 6x
= (x + 3)2
– 9
= (x + 3)2
– 6
+ 17 Troublemaker
+17
+ 3+ 3
+ 3

9. x2
– 4x
= (x – 2)2
– 4
= (x – 2)2
+ 5
x2
– 10x
= (x – 5)2
– 25
= (x – 5)2
– 22
+ 9
+9
+ 3+ 3
+ 3

10. x2
+ 8x
= (x + 4)2
– 16
= (x + 4)2
– 19
x2
– 12x
= (x – 6)2
– 36
= (x – 6)2
– 43
– 3
– 3
– 7
– 7

11. Completing The Square
Ex1 x2
+ 8x + 3
= (x + 4)2
– 16
= (x + 4)2
– 13
Ignore at first
½ of 8 42
+ 3

12. Completing The Square
Ex.2 x2
– 4x – 11
= (x – 2)2
– 4
= (x – 2)2
– 15
– 11

13. Key Question
x2
– 8x – 3
= (x – 4)2
– 16
= (x – 4)2
– 19
– 3

14. Nastier
2x2
+ 4x + 11

15. Nastier
2x2
+ 4x + 11
= 2(x2
+ 2x)+ 11

16. Nastier
2x2
+ 4x + 11
= 2(x2
+ 2x)
= 2 (x + 1)2
– 1
= 2(x + 1)2
= 2(x + 1)2
+ 9
+ 11
( )+ 11
– 2 + 11

17. Nastier
2x2
+ 12x – 13
= 2(x2
+ 6x)
= 2 (x + 3)2
– 9
= 2(x + 3)2
= 2(x + 3)2
– 31
– 13
( ) – 13
– 18 – 13

18. What is to be learned?
• How to complete the square
• How to use this to find maximum and
minimum values

19. Minimum Values
y = (x + 3)2
Lowest Value of y?
Try x = 0
y = (0 + 3)2
= 32
= 9

20. Minimum Values
y = (x + 3)2
Lowest Value of y?
Try x = -3
y = (-3 + 3)2
= 02
= 0
Minimum Value of y = 0,
when x = -3
corresponding
value of x

21. (x – 4)2
+ 7
Min Value?
Try x = 4
(4 – 4)2
+ 7
= 02
+ 7
= 7
Min Value 7,
Always get bracket bit equal to zero
when x = 4

22. Maximum Values
12 – (x – 5)2
Try x = 5
12 – 02
= 12
Maximum Value = 12, when x = 5
Often written in form –(x – 5)2
+ 12
Lowest value is zero

23. Putting it all together
Minimum value of
x2
+ 12x + 47
= (x + 6)2
– 36 + 47
= (x + 6)2
+ 11
Minimum value occurs when x =
Minimum Value is
Always get bracket
bit equal to zero

-6
11

24. Max and Min Values
Completing the square puts expressions in
form where it is easy to find max or min
value
Tactic is always to make bracket bit = 0
Ex y = x2
+ 10x + 7
= (x + 5)2
– 25 + 7
= (x + 5)2
– 18
so min value occurs when x = -5
y = -18

25. Key Question
Find the minimum value of expression and
corresponding value of x
y = x2
+ 10x + 7
= (x + 5)2
– 25 + 7
= (x + 5)2
– 18
so min value = -18
when x = -5