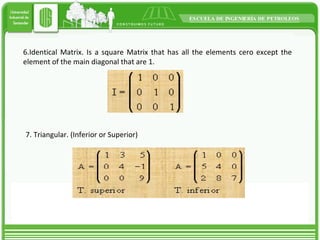
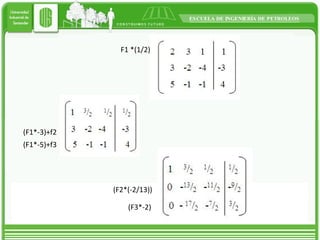
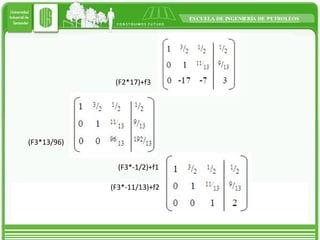
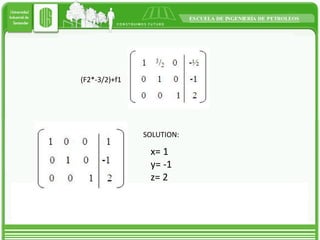
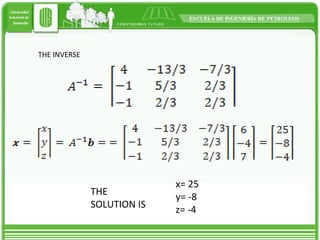
This document discusses different types of matrices and methods for solving linear equation systems. It describes rectangular, transposed, void, symmetric, diagonal, and identity matrices. It also explains the simple Gauss method which converts the matrix into upper triangular form and then back substitution to solve for unknown values. The Gauss-Jordan method converts the matrix into an identity matrix to more easily solve the system. Inverse matrices can also be used to solve systems by writing it as A*x=B and then calculating x as the inverse of A multiplied by B.

1. RUBEN DARIO ARISMENDI RUEDA

2. CHAPTER 4: ‘Direct Methods to solve lineal ecuation systems’

3. Types of Matrix. 1. RECTANGULAR:The Matrix that has different number of lines and columns mxn, Where ‘m’ is different of ‘n’. 2. Transpossition Matrix: Is the new matrix, that is obtain when the files and columns are changed.

4. 3.Void Matrix. When all the elements of the Matrix are cero. 4.Simetric Matrix. Is square matrix equal to the trnsposition matrix. 5.Diagonal Matrix. Is a square matriz with all the elements cero except the element of the main diagonal.

5. 6.Identical Matrix. Is a square Matrix that has all the elements cero except the element of the main diagonal that are 1. 7. Triangular. (Inferior or Superior)

6. 8. Inverse Matrix. A matrix is inverse when:

7. METHODS. SIMPLE GAUSS. This method has two main steps. a- Forward elimination: Consist in convert the Matrix into a Superior Triangular b- Backward sustitution: With the Inferior Matrix the last unkown value is obtained and then we have to start making substitutions.

8. We can change the order of the lines to make it easier to solve

9. F2-3f1 f3-5f1 F3-2f2

10. NOW WE START TO MAKE THE SUSTITUTIONS.

11. GAUSS-JORDAN. This method consist in treat the Matrix and convert it into a identical Matrix, and then is more easy to solve the system.

12. F1 *(1/2) (F1*-3)+f2 (F1*-5)+f3 (F2*(-2/13)) (F3*-2)

13. (F2*17)+f3 (F3*13/96) (F3*-1/2)+f1 (F3*-11/13)+f2

14. (F2*-3/2)+f1 x= 1 y= -1 z= 2 SOLUTION:

15. 3. Inverse Matrix. The inverse matrix could be used to solve a system as well. 2x + 4y + 3z = 6 y – z = - 4 3x + 5y + 7z =3 THE SYSTEM COULD BE WRITTEN LIKE A *x=B

16. THE INVERSE x= 25 y= - 8 z= -4 THE SOLUTION IS