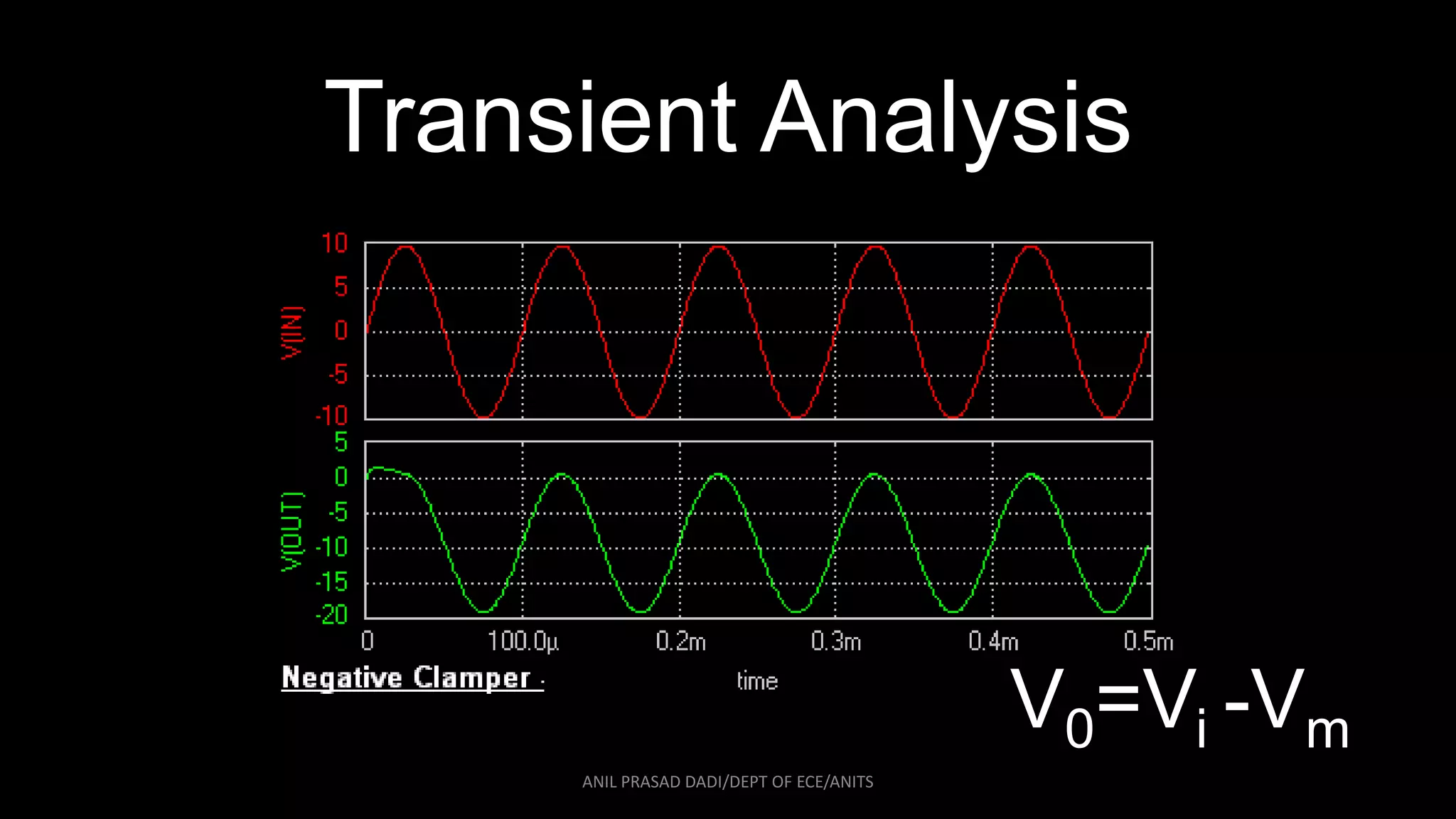
This document contains a detailed analysis of the transient response of a circuit containing a capacitor, diode, and resistors when subjected to a step input voltage VS. It analyzes the voltage and current values at different time intervals as the diode switches between forward and reverse biased states. Key points analyzed include the voltage across the capacitor VC, output voltage V0, and how they vary with time and the on/off state of the diode. Calculations are shown for V0 and VC at t=T/2, T, 3T/2, 2T, and 5T/2.

1. ANIL NEERUKONDA INSTITUTE OF TECHNOLOGY & SCIENCES(A)
Department of Electronics and Communication Engineering
ECE 216 Electronic circuits and Analysis-I
➢Academic year : 2020-21
➢Class & Section : 2/4 ECE-C
➢Name of the Faculty : Mr.D.Anil Prasad
ANIL PRASAD DADI/DEPT OF ECE/ANITS

2. ANIL NEERUKONDA INSTITUTE OF TECHNOLOGY & SCIENCES(A)
Department of Electronics and Communication Engineering
Non Linear Wave shaping circuits
Transient Analysis
ANIL PRASAD DADI/DEPT OF ECE/ANITS

3. Transient Analysis
ANIL PRASAD DADI/DEPT OF ECE/ANITS
V0=Vi +Vm

4. Transient Analysis
ANIL PRASAD DADI/DEPT OF ECE/ANITS
V0=Vi -Vm

5. ANIL PRASAD DADI/DEPT OF ECE/ANITS

6. Transient Analysis
VS
ANIL PRASAD DADI/DEPT OF ECE/ANITS
𝑇
2
T
3𝑇
2
2T
5𝑇
2
3T t0
10
RL
C
+
-
VS V0
RS
t=0+ VS=10V
VC(0
-)=0=VC(0+) Capacitor is initially uncharged
Diode is FB
+
-
RL
+
-
VS V0
RS
-
C
Rf
i
(+)0

7. Transient Analysis
VS
ANIL PRASAD DADI/DEPT OF ECE/ANITS
𝑇
2
T
3𝑇
2
2T
5𝑇
2
3T t
10
RL
C
+
-
VS V0
RS
t=0+ VS=10V
VC(0
-)=0=VC(0+) Capacitor is initially uncharged
Diode is FB
+
-
+
-
VS V0
RS
-
C
Rf
i
0
(+)0

8. +
-
Transient Analysis
VS
ANIL PRASAD DADI/DEPT OF ECE/ANITS
𝑇
2
T
3𝑇
2
2T
5𝑇
2
3T t
10
RL
C
+
-
VS V0
RS
t=0+ VS=10V
VC(0
-)=0=VC(0+) Capacitor is initially uncharged
Diode is FB
+
-
VS
V0
-
C Rs
Rf
+
V0=VS
𝑅𝑓
𝑅𝑓+𝑅𝑠
V0=10
100
100+100
V0=5V
5
i
0

9. Transient Analysis
VS
ANIL PRASAD DADI/DEPT OF ECE/ANITS
𝑇
2
T
3𝑇
2
2T
5𝑇
2
3T t
10
RL
C
+
-
VS V0
RS
+
-
0<t<T/2 VS=10V Diode is FB
V0(t)=Vf - (Vf-Vi)𝑒−
(𝑡−𝑡𝑖)
𝜏
Vf=0V ti=0 Vi=5V τ=(Rs+Rf)C
5
+
-
VS
V0
-
Rs
Rf
i
+
C
0

10. Transient Analysis
VS
ANIL PRASAD DADI/DEPT OF ECE/ANITS
𝑇
2
T
3𝑇
2
2T
5𝑇
2
3T t
10
RL
C
+
-
VS V0
RS
+
-
0<t<T/2 VS=10V Diode is FB
5
+
-
VS
V0
-
Rs
Rf
i
+
C
V0(t)=5𝑒−
𝑡
𝜏 V0(t=
𝑇
2
)=5𝑒−
𝑇
2𝜏 V0(t=
𝑇
2
)≈ 3V
0

11. Transient Analysis
VS
ANIL PRASAD DADI/DEPT OF ECE/ANITS
𝑇
2
T
3𝑇
2
2T
5𝑇
2
3T t
10
RL
C
+
-
VS V0
RS
+
-
0<t<T/2 VS=10V Diode is FB
5
+
-
VS
V0
-
Rs
Rf
i
+
V0(t=
𝑇
2
)=5𝑒−
𝑇
2𝜏 V0(t=
𝑇
2
)≈ 3V VC(t=
𝑇
2
)=?
+ VC -
VC(t=
𝑇
2
)= Vs − Vi VC(t=
𝑇
2
)= 10 − (3 + 3) VC(t=
𝑇
2
)= 4
VC(t=
𝑇
−
2
)=VC(t=
𝑇
+
2
)=4
Vi
-
+
0

12. + VC -
Transient Analysis
VS
ANIL PRASAD DADI/DEPT OF ECE/ANITS
𝑇
2
T
3𝑇
2
2T
5𝑇
2
3T t
10
RL
C
+
-
VS V0
RS
+
-
0<t<T/2 VS=10V Diode is FB
5
V0(t=
𝑇
2
)≈ 3V VC(t=
𝑇
−
2
)=VC(t=
𝑇
+
2
)=4 V0(t=
𝑇
+
2
)=?
t=
𝑇
+
2
VS=0V Diode is RB
RL
+
-
VS V0
RS
-
Rr
0
(+)0

13. + VC -
Transient Analysis
VS
ANIL PRASAD DADI/DEPT OF ECE/ANITS
𝑇
2
T
3𝑇
2
2T
5𝑇
2
3T t
10
RL
C
+
-
VS V0
RS
+
-
0<t<T/2 VS=10V Diode is FB
5
V0(t=
𝑇
2
)≈ 3V VC(t=
𝑇
−
2
)=VC(t=
𝑇
+
2
)=4 V0(t=
𝑇
+
2
)=?
V0(t=
𝑇
+
2
)= Vs − Vc
= 0 − 4 = −4 V0(t=
𝑇
+
2
)= -4V
t>
𝑇
+
2
VS=0V Diode is RB
RL
+
-
VS V0
RS
-
since drop across Rs≈0
0
+

14. -
-
+ +
RS
+
-
+
-
+ VC -
Transient Analysis
VS
𝑇
2
T
3𝑇
2
2T
5𝑇
2
3T t
10
RL
CVS V0
RS
-5
3
RLVS
V0
+
-
Rs
Rfi
+
VS
V0
C
0<t<T/2 VS=10 Diode FB
V0(t=
𝑇
2
)=5𝑒−
𝑇
2𝜏 V0(t=
𝑇
2
)≈ 3VV0(t)=5𝑒−
𝑡
𝜏
VC(t=
𝑇
−
2
)=VC(t=
𝑇
+
2
)=4
V0(t=
𝑇
+
2
)= Vs − Vc
t=
𝑇
+
2
VS=0V Diode is RB
Rs≈0
V0(t=
𝑇
+
2
)=?
V0(t=
𝑇
+
2
)= -4V
-4
0
ANIL PRASAD DADI/DEPT OF ECE/ANITS

15. +
Transient Analysis
VS
ANIL PRASAD DADI/DEPT OF ECE/ANITS
𝑇
2
T
3𝑇
2
2T
5𝑇
2
3T t
10
RL
C
+
-
VS V0
RS
+
-
5
-4
T/2<t<T VS=0V Diode is RB
V0(t)=Vf - (Vf-Vi)𝑒−
(𝑡−𝑡𝑖)
𝜏
Vf=0V ti=
𝑇
2
Vi= -4V τ=(Rs+RL)C
3
RS
-
+
-
+ VC - RLVS V0
0

16. +
Transient Analysis
VS
ANIL PRASAD DADI/DEPT OF ECE/ANITS
𝑇
2
T
3𝑇
2
2T
5𝑇
2
3T t
10
RL
C
+
-
VS V0
RS
+
-
5
-4
T/2<t<T VS=0V Diode is RB
3
RS
-
+
-
+ VC - RLVS V0V0(t)= -4𝑒−
(𝑡−
𝑇
2
)
𝜏 V0(T)= -4V
VC(t= T)= Vs − V0 VC(t= T)= 0 − −4 = 4V
VC(t= T -)= VC(t= T +) = 4V
0

17. Transient Analysis
VS
ANIL PRASAD DADI/DEPT OF ECE/ANITS
𝑇
2
T
3𝑇
2
2T
5𝑇
2
3T t
10
RL
C
+
-
VS V0
RS
+
-
5
-4
t=T+ VS=10V Diode is FB
V0(T)= -4V VC(t= T -)= VC(t= T +) = 4V
V0(T+)= ? Vi= Vs − Vc = 10 − 4 = 6V
V0(T+)= 3V
3
V0
+
T/2<t<T
i
0

18. Transient Analysis
VS
ANIL PRASAD DADI/DEPT OF ECE/ANITS
𝑇
2
T
3𝑇
2
2T
5𝑇
2
3T t
10
RL
C
+
-
VS V0
RS
+
-
5
-4
3
T<t<3T/2 VS=10V Diode is FB
V0(t)= 3𝑒−
(𝑡−𝑇)
𝜏
V0
V0(t=
3𝑇
2
)= 1.8V
Vc(t=
3𝑇
2
)= Vs-Vi Vc(t=
3𝑇
2
)= 10-(1.8+1.8)
Vc(t=
3𝑇
−
2
)= Vc(t=
3𝑇
+
2
)= 6.4
+
i
0

19. Transient Analysis
VS
ANIL PRASAD DADI/DEPT OF ECE/ANITS
𝑇
2
T
3𝑇
2
2T
5𝑇
2
3T t
10
RL
C
+
-
VS V0
RS
+
-
5
-4
3
V0(t=
3𝑇
+
2
)=?
t=
3𝑇
+
2
VS=0V Diode is RB
+
-
VS
-
Rs
RL
+
6.4V
V0
V0(t=
3𝑇
+
2
)=Vs-Vc =-6.4
V0(t)= 3𝑒−
(𝑡−𝑇)
𝜏 V0(t=
3𝑇
2
)= 1.8V
Vc(t=
3𝑇
−
2
)= Vc(t=
3𝑇
+
2
)= 6.4
T<t<3T/2 + -
0

20. Transient Analysis
VS
ANIL PRASAD DADI/DEPT OF ECE/ANITS
𝑇
2
T
3𝑇
2
2T
5𝑇
2
3T t
10
RL
C
+
-
VS V0
RS
+
-
5
-4
3
+
-
VS
-
Rs
RL
+
6.4V
V0V0(t=
3𝑇
+
2
)= -6.4
V0(t)= 3𝑒−
(𝑡−𝑇)
𝜏 V0(t=
3𝑇
2
)= 1.8V
Vc(t=
3𝑇
−
2
)= Vc(t=
3𝑇
+
2
)= 6.4
T<t<3T/2 + -
0

21. Transient Analysis
VS
ANIL PRASAD DADI/DEPT OF ECE/ANITS
𝑇
2
T
3𝑇
2
2T
5𝑇
2
3T t
10
RL
C
+
-
VS V0
RS
+
-
5
-4
3
+
-
VS
-
Rs
RL
+
C
V0
+ -3T/2<t<2T VS=0V Diode is RB
Vc(t=2T-)=Vs-V0=0-(-6.4)=6.4
Vf=0V ti=
3𝑇
2
Vi= -6.4V τ=(Rs+RL)C
V0(t)= -6.4𝑒−
(𝑡−
3𝑇
2 )
𝜏 V0(t=2T)= -6.4V
Vc(t=2T-)= Vc(t=2T+)= 6.4
0

22. Transient Analysis
VS
ANIL PRASAD DADI/DEPT OF ECE/ANITS
𝑇
2
T
3𝑇
2
2T
5𝑇
2
3T t
10
RL
C
+
-
VS V0
RS
+
-
5
-4
3
+
-
VS
-
Rs
Rf
+
+ 6.4 -
V0
3T/2<t<2T V0(t=2T-)= -6.4V
Vc(t=2T-)= Vc(t=2T+)= 6.4 V0(t=2T+)= ?
t=2T+ VS=10V Diode is FB
Vi=Vs-Vc =10-6.4=3.6
Vi
-
+
V0(t=2T+)= 1.8V
i
0

23. Transient Analysis
VS
ANIL PRASAD DADI/DEPT OF ECE/ANITS
𝑇
2
T
3𝑇
2
2T
5𝑇
2
3T t
10
RL
C
+
-
VS V0
RS
+
-
5
-4
3
+
-
VS
-
Rs
Rf
+
Vc
V0
-
2T<t<5T/2 VS=10 Diode is FB
Vi
-
+
Vf=0V ti= 2T Vi= 1.8V τ=(Rs+Rf)C
V0(t)= 1.8𝑒−
(𝑡−2𝑇)
𝜏 V0(
5𝑇
2
)= 1.1V
0

24. Transient Analysis
VS
ANIL PRASAD DADI/DEPT OF ECE/ANITS
𝑇
2
T
3𝑇
2
2T
5𝑇
2
3T t
10
RL
C
+
-
VS V0
RS
+
-
5
-4
3
+
-
VS
-
Rs
RL
+
7.8V
V0
-
2T<t<5T/2
Vi
-
+
V0(
5𝑇
2
)= 1.1V Vc(
5𝑇
−
2
)= Vc(
5𝑇
+
2
)= 7.8V V0(
5𝑇
+
2
)= ?
V0(t=
5𝑇
+
2
)= Vs − VC = 0 − 7.8
V0(t=
5𝑇
+
2
)= -7.8V
0
Since Rs≈0

25. Transient Analysis
VS
ANIL PRASAD DADI/DEPT OF ECE/ANITS
𝑇
2
T
3𝑇
2
2T
5𝑇
2
3T t
10
RL
C
+
-
VS V0
RS
+
-
5
-4
3
5T/2<t<3T VS=0 Diode is RB
Vf=0V ti=
5𝑇
2
Vi= -7.8V τ=(Rs+RL)C
V0(t)= -7.8𝑒−
(𝑡−
5𝑇
2
)
𝜏 V0(3T)= -7.8V
0

26. Transient Analysis
VS
ANIL PRASAD DADI/DEPT OF ECE/ANITS
𝑇
2
T
3𝑇
2
2T
5𝑇
2
3T t
10
RL
C
+
-
VS V0
RS
+
-
5
-4
3
5T/2<t<3T
V0(3T)= -7.8V
Vc(3T)=VS-V0=0-(-7.8)=7.8V
Vc(3T-)= Vc(3T+)= 7.8V
0

27. Transient Analysis
VS
ANIL PRASAD DADI/DEPT OF ECE/ANITS
𝑇
2
T
3𝑇
2
2T
5𝑇
2
3T t
10
RL
C
+
-
VS V0
RS
+
-
5
-4
3
V0(3T)= -7.8V Vc(3T-)= Vc(3T+)= 7.8V
V0(3T+)= ?
t=3T+ VS=10V Diode is FB
Vi=Vs-Vc =10-7.8=2.2
V0(t=3T+)= 1.1V
5T/2<t<3T
0

28. Transient Analysis
VS
ANIL PRASAD DADI/DEPT OF ECE/ANITS
𝑇
2
T
3𝑇
2
2T
5𝑇
2
3T
7𝑇
2
t
10
RL
C
+
-
VS V0
RS
+
-
5
-4
3
V0(3T+)= 1.1V
V0(
7𝑇
2
)= 0.66 Vc(
7𝑇
2
)= 8.68V
t=
7𝑇
2 VS=0V Diode is RB
V0=Vs-Vc =0-8.68=-8.68
V0(t=
7𝑇
+
2
)= -8.68V
3T<t<7T/2
0

29. Transient Analysis
VS
ANIL PRASAD DADI/DEPT OF ECE/ANITS
𝑇
2
T
3𝑇
2
2T
5𝑇
2
3T
7𝑇
2
t
10
RL
C
+
-
VS V0
RS
+
-
5
-4
3
0

30. The clamping circuit Theorem
• The clamping circuit theorem states that under steady-state
conditions for any input waveform, the ratio of the area under the
output voltage curve in the forward direction to that in the reverse
direction is equal to the ratio Rf /RL.
• This theorem enables us to find the voltage level to which the output is
clamped.
ANIL PRASAD DADI/DEPT OF ECE/ANITS
𝐴𝑓
𝐴𝑟
=
𝑅𝑓
𝑅 𝐿

31. The clamping circuit Theorem
• To derive the clamping circuit theorem, consider a typical steady-state
output for the clamping circuit
ANIL PRASAD DADI/DEPT OF ECE/ANITS

32. The clamping circuit Theorem
• In the interval t1 to t2 D is ON. Hence during this period, the charge builds
up on the capacitor C.
• Let if is the diode current , the charge gained by the capacitor during the
interval t1 to t2 is:
ANIL PRASAD DADI/DEPT OF ECE/ANITS
q1= ‫׬‬𝑡1
𝑡2
𝑖 𝑓 𝑑𝑡 =
1
𝑅 𝑓
‫׬‬𝑡1
𝑡2
𝑉𝑓 𝑑𝑡

33. The clamping circuit Theorem
• In the interval t2 to t3 D is OFF. Hence the capacitor discharges and charges
lost by C is:
ANIL PRASAD DADI/DEPT OF ECE/ANITS
q2= ‫׬‬𝑡2
𝑡3
𝑖 𝑟 𝑑𝑡 =
1
𝑅 𝐿
‫׬‬𝑡2
𝑡3
𝑉𝑟 𝑑𝑡

34. The clamping circuit Theorem
• At steady-state, the charge gained is equal to the charge lost. In other
words, q1 = q2
ANIL PRASAD DADI/DEPT OF ECE/ANITS
1
𝑅 𝑓
‫׬‬𝑡1
𝑡2
𝑉𝑓 𝑑𝑡=
1
𝑅 𝐿
‫׬‬𝑡2
𝑡3
𝑉𝑟 𝑑𝑡
𝐴𝑓 = න
𝑡1
𝑡2
𝑉𝑓 𝑑𝑡
𝐴𝑟 = න
𝑡2
𝑡3
𝑉𝑟 𝑑𝑡
𝐴𝑓
𝑅𝑓
=
𝐴𝑟
𝑅 𝐿
q1=
1
𝑅 𝑓
‫׬‬𝑡1
𝑡2
𝑉𝑓 𝑑𝑡
q2=
1
𝑅 𝐿
‫׬‬𝑡2
𝑡3
𝑉𝑟 𝑑𝑡
𝐴𝑓
𝐴𝑟
=
𝑅𝑓
𝑅 𝐿

35. Problem #1
• A unsymmetrical square wave with T1=1ms and T2=1us has an amplitude of 10V. This
signal is applied to the circuit shown in figure Rf=50 RL=50K. Find the level to which
output is clamped to
ANIL PRASAD DADI/DEPT OF ECE/ANITS
T1
T2
0 V1
RL
C
-
VS V0
-
+ +
Af
Ar
10V

36. T1
Problem #1
• A unsymmetrical square wave with T1=1ms and T2=1us has an amplitude of 10V. This
signal is applied to the circuit shown in figure Rf=50 RL=50K
ANIL PRASAD DADI/DEPT OF ECE/ANITS
T2
0 V1
RL
C
-
VS V0
-
+ +
Af
Ar
𝐴𝑓
𝐴𝑟
=
𝑉1 𝑥𝑇1
10 − 𝑉1 𝑥𝑇2
=
𝑉1 𝑥1000μ
10 − 𝑉1 𝑥1μ
𝑅𝑓
𝑅 𝐿
=
50
50𝐾
=10-3 𝐴𝑓
𝐴𝑟
=
𝑅𝑓
𝑅 𝐿
𝑉1 𝑥1000
10−𝑉1 𝑥1
=10-3 V1=10-5
10V
(10-V1)

37. Problem #2
• A unsymmetrical square wave with T1=1us and T2=1ms has an amplitude of 10V. This
signal is applied to the circuit shown in figure Rf=50 RL=50K
ANIL PRASAD DADI/DEPT OF ECE/ANITS
T2
T1
0
V1
RL
C
-
VS V0
-
+ +
Af
Ar
𝐴𝑓
𝐴𝑟
=
𝑉1 𝑥𝑇1
10 − 𝑉1 𝑥𝑇2
=
𝑉1 𝑥1μ
10 − 𝑉1 𝑥1000μ
𝑅𝑓
𝑅 𝐿
=
50
50𝐾
=10-3 𝐴𝑓
𝐴𝑟
=
𝑅𝑓
𝑅 𝐿
𝑉1 𝑥1
10−𝑉1 𝑥1000
=10-3 V1=5V
10V
(10-V1)

38. Problem #3
• A unsymmetrical square wave with T1=1ms and T2=1us has an amplitude of 10V. This
signal is applied to the circuit shown in figure Rf=50 RL=50K
ANIL PRASAD DADI/DEPT OF ECE/ANITS
T2
T1
0
V1
RL
C
-
VS V0
-
+ +
Af
Ar
𝐴𝑓
𝐴𝑟
=
𝑉1 𝑥𝑇1
10 − 𝑉1 𝑥𝑇2
=
𝑉1 𝑥1000𝑢
10 − 𝑉1 𝑥1μ
𝑅𝑓
𝑅 𝐿
=
50
50𝐾
=10-3 𝐴𝑓
𝐴𝑟
=
𝑅𝑓
𝑅 𝐿
𝑉1 𝑥1000
10−𝑉1 𝑥1
=10-3
V1=10-5V
10V(10-V1)

39. 5V
Design of diode clamper
• Design a diode clamper to restore the positive peaks of the input signal to a voltage level
of 5V. Assume Vγ=0.5V f=1KHz, Rf=1K Rr=200K and RLC=10T
• When diode conducts
❑RL>>Rf
❑Let RL=kRf
• When diode doesn’t conduct
❑Rr>>RL
❑Let Rr=kRL
ANIL PRASAD DADI/DEPT OF ECE/ANITS
RL
C
-
VS V0
-
+ +
RL =
R𝑟
RL
𝑅 𝑓

40. 5V
Design of diode clamper
• Design a diode clamper to restore the positive peaks of the input signal to a voltage level
of 5V. Assume Vγ=0.5V f=1KHz, Rf=1K Rr=200K and RC=10T
ANIL PRASAD DADI/DEPT OF ECE/ANITS
RL
C
-
VS V0
-
+ +
RL =
R𝑟
RL
𝑅 𝑓
R2
L = 𝑅 𝑟 𝑅 𝑓
RL = 𝑅 𝑟 𝑅 𝑓 RL = 14.14KΩ
RC=10T C=
10x1
f xRL
C=0.707μF
Let VR=VR1+ Vγ Where VR1=5V is given VR=5+0.5=5.5V