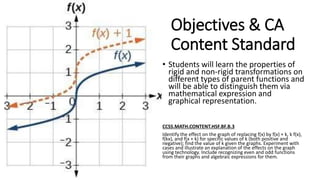
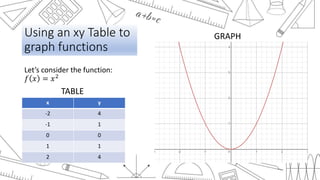
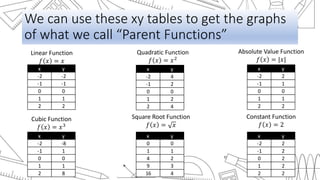
This document discusses transformations of functions. It begins by introducing common parent functions like linear, quadratic, absolute value, cubic and square root functions using xy-tables and graphs. It then demonstrates how adding or subtracting values like 1, 5, or 2 to a quadratic function f(x)=x^2 results in a rigid transformation that shifts the graph up, down, left or right but maintains the same basic shape. The document defines rigid transformations as those that only change the position of the graph and lists the three types as vertical shifts, horizontal shifts, and reflections, providing formulas for shifting graphs vertically and horizontally.

1. Transformations
of Functions
Mr. Johnson
Algebra 1
California Content Standard – Building Functions

2. Objectives & CA
Content Standard
• Students will learn the properties of
rigid and non-rigid transformations on
different types of parent functions and
will be able to distinguish them via
mathematical expression and
graphical representation.
CCSS.MATH.CONTENT.HSF.BF.B.3
Identify the effect on the graph of replacing f(x) by f(x) + k, k f(x),
f(kx), and f(x + k) for specific values of k (both positive and
negative); find the value of k given the graphs. Experiment with
cases and illustrate an explanation of the effects on the graph
using technology. Include recognizing even and odd functions
from their graphs and algebraic expressions for them.

3. Before We Begin, Let’s Recap
What do we know about
functions?
Spend 2-3 minutes
discussing with your
classmates in groups of 4
EVERYTHING you can think
about regarding functions.
We will then write down
one thing from each group
together as a class.

4. Using an xy Table to
graph functions
Let’s consider the function:
𝑓 𝑥 = 𝑥2
TABLE
x y
-2 4
-1 1
0 0
1 1
2 4
GRAPH

5. We can use these xy tables to get the graphs
of what we call “Parent Functions”
x y
-2 -2
-1 -1
0 0
1 1
2 2
x y
-2 4
-1 2
0 0
1 2
2 4
x y
-2 2
-1 1
0 0
1 1
2 2
x y
-2 -8
-1 1
0 0
1 1
2 8
x y
0 0
1 1
4 2
9 3
16 4
x y
-2 2
-1 2
0 2
1 2
2 2
Linear Function
𝑓 𝑥 = 𝑥
Quadratic Function
𝑓 𝑥 = 𝑥2
Absolute Value Function
𝑓 𝑥 = |𝑥|
Cubic Function
𝑓 𝑥 = 𝑥3
Square Root Function
𝑓 𝑥 = 𝑥
Constant Function
𝑓 𝑥 = 2

6. We can use these xy tables to get the graphs
of what we call “Parent Functions”
Linear Function
𝑓 𝑥 = 𝑥
Quadratic Function
𝑓 𝑥 = 𝑥2
Absolute Value Function
𝑓 𝑥 = |𝑥|
Cubic Function
𝑓 𝑥 = 𝑥3
Square Root Function
𝑓 𝑥 = 𝑥
Constant Function
𝑓 𝑥 = 2

7. What happens if we add a one to the function? 𝑓 𝑥 = 𝑥2 + 1
What if we add 5? 𝑓 𝑥 = 𝑥2 + 5
How about if we subtract 2? 𝑓 𝑥 = 𝑥2
− 2
Revisiting the function
𝑓 𝑥 = 𝑥2

8. GROUP ACTIVITY!
• Fill the following xy tables with your group mates and make a
corresponding graph. Discuss with each other any similarities you
have found between these three new quadratic functions and the
parent function.
x y
-2
-1
0
1
2
x y
-2
-1
0
1
2
x y
-2
-1
0
1
2
𝑓 𝑥 = 𝑥2 + 1 𝑓 𝑥 = 𝑥2 + 5 𝑓 𝑥 = 𝑥2 − 2

9. What did you notice?
• This is an example of a RIGID TRANSFORMATION
• A RIGID TRANSFORMATION is a transformation in which the basic shape of
the graph is unchanged
• RIGID TRANSFORMATIONS change only the position of the graph in the
coordinate plane

10. Types of RIGID TRANSFORMATIONS
• There are 3 types of RIGID TRANSFORMATIONS
1. VERTICAL SHIFTS
2. HORIZONTAL SHIFTS
3. REFLECTIONS

11. VERTICAL & HORIZONTAL SHIFTS
Let 𝑐 be some positive real number. We can determine VERTICAL &
HORIZONTAL SHIFTS with the following formulas:
VERTICAL SHIFT 𝑐 units upward:
𝑔 𝑥 = 𝑓 𝑥 + 𝑐
VERTICAL SHIFT 𝑐 units downward:
𝑔 𝑥 = 𝑓 𝑥 − 𝑐
HORIZONTAL SHIFT 𝑐 units to the right:
𝑔 𝑥 = 𝑓(𝑥 − 𝑐)
HORIZONTAL SHIFT 𝑐 units to the left:
𝑔 𝑥 = 𝑓(𝑥 + 𝑐)