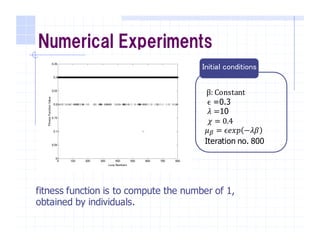
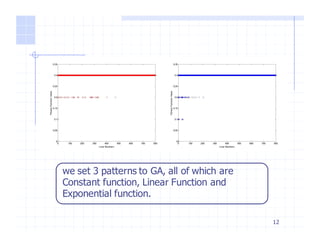
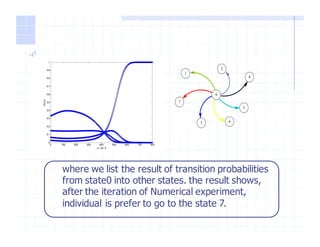
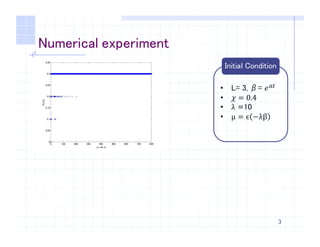
This document discusses applying nonlinear stochastic optimal control (NSOC) theory to genetic algorithms (GA). It provides an overview of GA and NSOC, describes modeling GA as a discrete-time controlled Markov process within the NSOC framework, and presents the results of a numerical experiment applying the NSOC-described GA to optimization problems. The experiment shows the transition probabilities between states after 800 iterations, indicating individuals prefer moving to state 7. The document concludes by noting future work could improve the fitness function and computation speed when applying NSOC to GA.

1. Application of Nonlinear Stochastic
Optimal Control for Genetic Algorithm
計画数理講座
丁 可
2014.02.14

2. Construction
1. Introduction
2. Overview of Genetic Algorithm
3. Nonlinear Stochastic Optimal Control
4. Application of NSOC for GA
5. Numerical Experiments
6. Conclusion
2

3. NSOC
GA
Application
3
Introduction
Background
u Nonlinear Stochastic Optimal Control
Foundation problem for control theory
u Genetic Algorithm
Derived from the principles of Darwinian natural
selection and evolution.
Previous research
uMarkov Chain Analysis on Simple Genetic Algorithms
Suzuki Joe (1995)
uLinearly-Solvable Markov Decision Problems
E. Todorov (2006)

4. 4
Overview of Genetic Algorithms
0
1
1
0
0
1
0
1
1
0
0
1
1
0
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1

5. Algorithm of GA
5
1. Obtain two parents by the selection function.
2. Produce their child by the crossover function
3. Mutate it by the mutation function.
4. Put the result into the next generation.
5. less than population members, go to Step 1.
l Optimization
l Automatic Programming
l Economic Models
l Social Systems Models
0
1
1
0
1
0
0
1

6. Nonlinear Stochastic Optimal
Control(NSCO)
Continuous Model
𝑥⃗ are given at an initial time t , the SCO problem is to find the
control path 𝑢 ' can minimized. the cost to go function is
continuous-time stochastic dynamics
d) = 𝑓 𝑋, 𝑢 𝑑/ + 𝐹 𝑥, 𝑢 𝑑2
optimal control law is
𝑢∗ = −𝜎6 𝐵 𝑥 8 𝜐)(𝑋)
6
𝐽(𝑥⃗,𝑡) = min
A
→
𝐶(𝑥⃗, 𝑡, 𝑢 ('))
𝑥 ∈ ℝFGstate vector
𝑢 ∈ ℝFAcontrol vector
𝜔 ∈ ℝFPBrown motion

7. Discrete Model
7
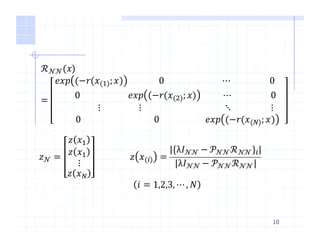
when we let 𝑝 𝑥T
𝑥, 𝑢 = 𝑢 𝑥T
𝑥
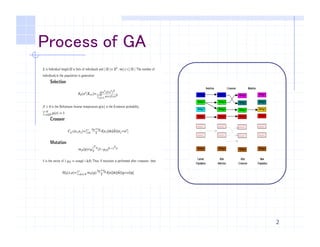
The bellman function of υ 𝑥 can write as
υ 𝑥 = min
V∈𝒰 X
{ℓ 𝑖, 𝑢 + EX]~_ ' 𝑥, 𝑢 𝜐(𝑥T
) }
optimal action will be
𝑢∗ 𝑥T 𝑥 =
𝑝 𝑥T 𝑥 𝓏 𝑥T
𝒢 𝓏 𝑥
𝓏 𝑥 = exp −𝑞 𝑥 𝒢 𝓏 𝑧 𝓏 = 𝑄𝑃𝓏
action cost of
current state
the value function
of next state

8. Application of NSOC for GA
Transition probability of GA
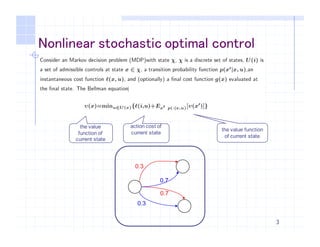
Selection
𝑆j 𝑥T
𝑝 =
𝑓 𝑥T j
∑ 𝑓 𝑥 j
X∈_
Crossover𝐶X] 𝑥l, 𝑥m = ∑
nopnqo
6r 𝛿 𝑥l ⊗ 𝑘 ⊕ 𝑘w ⊗ 𝑥m = 𝑥T
Mutation
8
𝑚j ℎ = 𝜇j
{|}
(1 − 𝜇j)~•{|}
β ∶ Blotzman invese T
𝜇j = ϵ𝑒𝑥𝑝 −𝜆𝛽
ℎ mutation mask
𝑘 Crossover mask
𝑝 𝑥T 𝑥 = • 𝑆j 𝑦 𝑝
•
• 𝑚j 𝑥,ℎ{ 𝑚j(𝑦,ℎ6
}•,}‘
)
𝐶X] 𝑥l, 𝑥m •
𝜒r + 𝜒̅r
2
r
𝛿 (𝑥 ⊕ ℎ{)⊗ 𝑘 ⊕ 𝑘w ⊗ (𝑦 ⊕ ℎ6 = 𝑥T

9. Describe GA by NSC
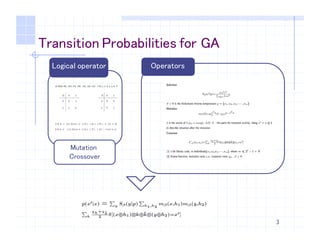
let 𝑝 𝑥T 𝑥, 𝑢 = 𝑢 𝑥T 𝑥 = 𝑝 𝑥T 𝑥 𝑒𝑥𝑝 𝑢X];X
we can get eigenvalue function is
9
λ𝑧— = 𝒫 𝒩𝒩 𝑥 ℛ 𝒩𝒩 𝑥 𝑧 𝒩 (∀𝒙)
𝒫 𝒩𝒩(𝑥) =
𝑝 𝑥({) 𝑥 𝑝 𝑥(6) 𝑥 ⋯ 𝑝 𝑥(—) 𝑥
𝑝 𝑥({) 𝑥 𝑝 𝑥(6) 𝑥 ⋯ 𝑝 𝑥(—) 𝑥
⋮ ⋮ ⋱ ⋮
𝑝 𝑥({) 𝑥 𝑝 𝑥(6) 𝑥 ⋯ 𝑝 𝑥(—) 𝑥
0
0
0
0
0
1
0
1
1
1
0
0
1
0
1
1
1
0
0
1
0
1
1
1

10. 10
ℛ 𝒩𝒩(𝑥)
=
𝑒𝑥𝑝 (−𝑟(𝑥 { ; 𝑥) 0 ⋯ 0
0 𝑒𝑥𝑝 (−𝑟(𝑥 6 ; 𝑥) ⋯ 0
⋮ ⋮ ⋱ ⋮
0 0 𝑒𝑥𝑝 (−𝑟(𝑥 — ; 𝑥)
𝑧 𝒩 =
𝑧 𝑥{
𝑧 𝑥{
⋮
𝑧 𝑥—
𝑧 𝑥(l) =
|{λ𝐼 𝒩𝒩 − 𝒫 𝒩𝒩ℛ 𝒩𝒩}l|
|λ𝐼 𝒩𝒩 − 𝒫 𝒩𝒩ℛ 𝒩𝒩|
𝑖 = 1,2,3, ⋯, 𝑁

11. Numerical Experiments
β: Constant
ϵ =0.3
𝜆 =10
𝜒 = 0.4
𝜇j = ϵ𝑒𝑥𝑝 −𝜆𝛽
Iteration no. 800
fitness function is to compute the number of 1,
obtained by individuals.
Initial conditions

12. 12
we set 3 patterns to GA, all of which are
Constant function, Linear Function and
Exponential function.

13. where we list the result of transition probabilities
from state0 into other states. the result shows,
after the iteration of Numerical experiment,
individual is prefer to go to the state 7.
0
2
3
4
5 6
7
1

14. Introduce theory of GA
Introduce theory of NSOC
Conclusion
5
Overview of previous works
Across the discrete model of NSOC, we apply
it into GA , showed in numerical results.
Future Works
fitness function should
be change by complex
Compute speed should
be improved.
Apply by NSOC

15. Thank you for your kind attention
15

16. 2
Process of GA

17. 3
Nonlinear stochastic optimal control
the value
function of
current state
the value function
of current state
action cost of
current state

18. 3
Nonlinear stochastic optimal control

19. 3
Nonlinear stochastic optimal control

20. 3
Transition Probabilities for GA
Logical operator Operators
Mutation
Crossover

21. Eigenvalue function

22. 22

23. 23

24. • L= 3, β= 𝑒¨/
• 𝜒 = 0.4
• λ =10
• µ = ϵ −λβ
3
Numerical experiment
Initial Condition

25. 25