Topology for Computing: Homology

Topology for Computing
Chapter 4. Homology
Sangwoo Mo
TDA Study
October 16, 2017
Sangwoo Mo (TDA Study) Chap 4. Homology October 16, 2017 1 / 37

Table of Contents
1 Motivation
2 Euler characteristic
3 Homotopy
4 Homology

Table of Contents
1 Motivation
3 Homotopy
4 Homology

Classifying Topological Spaces
How to classify topological spaces?
1-manifold has only two types: line and loop
How about higher-dimension manifolds?
The natural way is equivalence class of homeomorphism
Homeomorphism preserves topology by deﬁnition
However, it is hard to ﬁnd homeomorphism in general
Thus, we will classify spaces by topological invariants e.g.
Euler characteristic
Homotopy
Homology (our main focus)

Table of Contents
1 Motivation
3 Homotopy
4 Homology

Deﬁnition (Euler characteristic of simplicial complex)
Let K be a simplicial complex and si = card{σ ∈ K | dim σ = i}. The
Euler characteristic of K is
χ(K) =
dim K
i=0
(−1)i
si =
σ∈K−{∅}
(−1)dim σ
.
Deﬁnition (Euler characteristic of manifold)
Given any triangulation K of a manifold M, χ(K) is invariant. We call
χ(M) = χ(K) be the Euler characteristic of M.

Example (basic 2-manifolds)
Here are some popular 2-manifolds. Sphere S2, torus T2, real projective
plane RP2
, and the Klein bottle K2, respectively.
FYI 1: M¨obius strip is homeomorphic to one point removed RP2
.
FYI 2: Klein bottle is homeomorphic to connected sum of two RP2
s.

Example (χ of basic 2-manifolds)
We can compute the Euler characteristic of basic 2-manifolds by
triangulation of the diagram.
Moreover, we can extend this result to the general closed 2-manifolds by
connected sum of basic 2-manifolds.

Connected Sum
Deﬁnition (connected sum)
The connected sum of two n-manifolds M1, M2 is
M1 # M2 = M1 − ˚Dn
1
∂˚Dn
1 =∂˚Dn
2
M2 − ˚Dn
2
where ˚Dn
1 , ˚Dn
2 are n-dimensional closed disks in M1, M2, respectively.
Example (connected sum of torus)
Connected sum of 2 tori. We call it genus 2 torus.

Connected Sum
Theorem (χ of connected sum)
For compact surfaces M1, M2,
χ(M1 # M2) = χ(M1) + χ(M2) − 2.
Corollary (χ of connected sum of T2
/RP2
)
As corollary, χ(gT2) = 2 − 2g and χ(gRP2
) = 2 − g.

Classification of 2-manifolds
We can prove that any closed surface are homeomorphic to the connected
sum of T2 or the connected sum of RP2
. (Sphere is genus 0 torus.)
Theorem (classification of 2-manifolds)
The closed 2-manifold M is homeomorphic to
the connected sum of T2 if it is orientable
the connected sum of RP2
if it is not orientable
Using Euler characteristic, we can also identify the number of connection.
Homeomorphism (and Euler characteristic) suceed to classify 2-manifolds.
However, we need better tools to classify higher-dimension manifolds.
Before we move on, we will introduce basic category theory to formally
define invariant, from topological space to algebraic structure.

Basic Category Theory
Deﬁnition (category)
A category C consists of:
(a) a collection Ob(C) of objects
(b) sets Mor(X, Y ) of morphisms for each pair X, Y ∈ Ob(C); including a
distinguished identity morphism 1 = 1X ∈ Mor(X, Y ) for each X
(c) a composition of morphisms function ◦ : Mor(X, Y ) × Mor(Y , Z)
→ Mor(X, Z) for each triple X, Y , Z ∈ Ob(C), satisfying
f ◦ 1 = 1 ◦ f = f , and (f ◦ g) ◦ h = f ◦ (g ◦ h)
Deﬁnition (functor)
A (covariant) functor F from a category C to a category D assigns
(a) object X ∈ C to an object F(X) ∈ D
(b) morphism f ∈ Mor(X, Y ) to a morphism F(f ) ∈ Mor(F(X), F(Y ));
such that F(1) = 1 and F(f ◦ g) = F(f ) ◦ F(g)

Example (examples of category)

Example (visual illustration of functor)
F is a functor mapping category of 2-manifolds to category of 1-manifolds.

Functor from Topology to Algebra
Transform diﬃcult topological object to well-known algebraic object.
object: topological space → group & module
morphism: homeomorphism → isomorphism (not really!)
Homotopy and homology are easier to compute, but less discriminative
homology ⊂ homotopy ⊂ homeomorphy

Table of Contents
1 Motivation
3 Homotopy
4 Homology

Homotopy
Deﬁnition (homotopy)
The homotopy of two continuous functions f , g : X → Y is a continuous
function H : X × [0, 1] → Y such that H(x, 0) = f (x) and H(x, 1) = g(x)
for x ∈ X. We can think H as a continuous deformation of f into g.
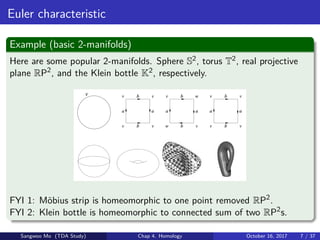
Example (homotopy vs homeomorphy)
X and Y are homotopy equivalent, but not homeomorphic.

Homotopy
Deﬁnition (homotopy group)
Choose base point s ∈ Sn and x ∈ X. The homotopy group πn(X, x) is
the set of homotopy classes of maps f : (Sn, s) → (X, x). For simply
connected space, πn(X, x) is independent to x, thus we can write πn(X).
We call π1(X) be the fundamental group.
Remark (homotopy ‘group’)
Remark that πn(X) has a group structure. Even more, for n ≥ 2, πn(X)
becomes an abelian group.

Homotopy
Intuitively, homotopy group counts the number of loops
Example (fundamental group of torus)
The fundamental group of torus is π1(T2) = Z × Z.

Undecidability of Homeomorphy/Homotopy
Theorem (undecidability of homeomorphy/homotopy)
For manifolds with dimension higher than 4, homeomorphy/homotopy
problem is undecidable.
Proof sketch (Markov’s construction).
For given group, construct a corresponding manifold using Dehn surgery.
It reduces the homeomorphy/homotopy problem to the group isomorphism
problem, which is known to be undecidable.

Limitation of Homotopy
Homotopy group is one way to classify topological spaces
However, it has several problems:
not combinatorial
hard to compute
inﬁnite description of πn(X)
⇒ It motivates the homology, the combinatorial computable functor with
ﬁnite description

Table of Contents
1 Motivation
3 Homotopy
4 Homology

Homology
There are several ways to define homology (e.g. CW-complex), but we will
only cover simplicial homology; We only consider a simplicial complex K
First, we will define chain and cycle, the extension of path and loop
Definition (chain group)
The kth chain group Ck(K), + of K is the free abelian group on the
oriented k-simplices. An element of Ck(K) is a k-chain,
c =
q
nq[σq], nq ∈ Z, σq ∈ K.

Homology
Deﬁnition (boundary homomorphism)
The boundary homomorphism ∂k : Ck(K) → Ck−1(K) is
∂kσ =
i
(−1)i
[v0, v1, ..., ˆvi , ..., vn]
where ˆvi indicates that vi is deleted from the sequence.
Example (boundary homomorphism of simplices)
∂1[a, b] = b − a
∂2[a, b, c] = [b, c] − [a, c] + [a, b]
∂3[a, b, c, d] = [b, c, d] − [a, c, d] + [a, b, d] − [a, b, c]

Homology
Deﬁnition (chain complex)
The chain complex C∗ is a sequence of chain groups
0 −→ Cn
∂n
−→ Cn−1 −→ ... −→ C1
∂1
−→ C0
∂0
−→ 0
Deﬁnition (cycle, boundary)
The kth cycle group is Zk = ker ∂k and the kth boundary group is
Bk = im ∂k+1. Elements of Zk and Bk are cycle and boundary.

Homology
Theorem (nesting of cycle/boundary group)
Zk and Bk are free abelian normal subgroup of Ck such that
Bk ≤ Zk ≤ Ck. Here, Bk ≤ Zk since ∂k−1∂k = 0.

Homology
Definition (homology group)
The kth homology group is
Hk = Zk/Bk = ker ∂k/im ∂k−1.
Note that homology groups are finitely generated abelian.
Definition (Betti number)
The kth Betti number βk = βk(Hk) is the rank of the free part of Hk.

Understanding Homology
For simplicity, we only consider subcomplexes of S3
Subcomplexes of S3 easy to handle (torsion-free)
Algorithmically, simple one point compactiﬁcation converts R3 to S3
For 3-dim torsion-free space, Betti numbers have intuitive meaning
Alexander Duality:
β0 measures the number of components
β1 measures the number of tunnels
β0 measures the number of voids

Understanding Homology
Example (Alexander duality)
Homology of basic 2-manifolds.

Invariance
We hope homology be invariant for same underlying space
First approach was proving that any two triangulations of a
topological space have a common reﬁnement (Hauptvermutung)
However, it was false for manifolds of dimension ≥ 5
For general spaces, singular homology is introduced
Simplical homology is equivalent to singular homology
Algorithmically, we can just compute (easy) simplical homology

Relation to Euler characteristic
The sequence of homology groups also forms a chain complex
0 −→ Hn −→ Hn−1 −→ ... −→ H1 −→ H0 −→ 0
Deﬁnition (Euler charactersitic of chain complex)
The Euler charactersitic of chain complex C∗ is
χ(C∗) =
i
(−1)i
rank(Ci ).
Theorem (Euler-Poincar´e formula)
χ(C∗) = χ(H∗(C∗)) =
i
(−1)i
βi .

Relation to Homotopy
Theorem (Hurewicz theorem)
For any space X and positive integer k there is a group homomorphism
h∗ : πk(X) → Hk(X).
If X is (n − 1)-connected, h∗ is an isomorphism for all 2 ≤ k ≤ n and
abelinization for n = 1. In particular, the theorem says that
H1(X) ∼= π1(X)/[π1(X), π1(X)].

Homology with coefficients
We assumed chain group be the free abelian group, which is Z-module
We may replace this ring with any PID D, such as Z2
Definition (homology with coefficients)
The kth homology with ring of coefficients D is
Hk(K; D) = Zk(K; D)/Bk(K; D).
Our goal is to compute Hk(K; D) for arbitrary D, using Hk(K)
If we use Z2, the computation becomes greatly simple (see Chap 7.)

Deﬁnition (short exact sequence)
The short exact sequence is seqeunce of groups
0
ϕ3
−→ A
ϕ2
−→ B
ϕ1
−→ C
ϕ0
−→ 0
such that im ϕi = ker ϕi−1.
Theorem (splitting lemma)
For short exact sequence, B ∼= A × C.

Theorem (universal coeﬃcient theorem)
Let G be an Abelian. Then following sequence is short exact
0 → Hk(K) ⊗ G → Hk(K; G) → Hk−1(K) ∗ G → 0
where ⊗ is tensor product and ∗ is torsion product.

Using universal coeﬃcient theorem and splitting lemma, we can derive
Hk(K; D) for some special cases
Example (homology with coeﬃcients)
1. Case Hk(K; Zp):
Hk(K; Zp) ∼= (Hk(K; Zp) ⊗ Zp) × (Hk(K; Zp) ∗ Zp)
∼= torsion part × (Zp)βk
2. Case Hk(K; F):
Hk(K; F) ∼= (Hk(K; F) ⊗ F) × (Hk(K; F) ∗ F) ∼= Fβk

Questions?

Topology for Computing: Homology

More Related Content

What's hot

Similar to Topology for Computing: Homology

More from Sangwoo Mo

Recently uploaded

Topology for Computing: Homology