Topological Data Analysis and Persistent Homology

Topological Data Analysis and
Persistent Homology
Supervisor: Prof. Francesco Vaccarino, Candidate: Carla Federica Melia
POLITECNICO DI TORINO
DIPARTIMENTO DI SCIENZE MATEMATICHE
Corso di Laurea Magistrale in Ingegneria Matematica
Graduation Session of December 2018
A.Y. 2017/18

 Topological Data Analysis (TDA) is a branch of applied mathematics that uses
notions and techniques of a miscellaneous set of scientific fields such as
 Its resulting tools allow to infer robust features about the “shape” of complex
datasets potentially corrupted by noise/incompleteness.
2
Introduction
Topological Data Analysis and Persistent Homology - Politecnico di Torino - 2018
StatisticsComputer ScienceAlgebraic Topology

TDA aims at inferring statistically significative information on the shape of the data.
3
The Shape of Data
[1]

[15] [16]
4
Finding Loops and Voids in Universe

Periodic behaviors Attractors
[7] [8]
5
Periodic Systems

6
Effective Brain Networks Analysis
[17][5]

 This thesis focuses on Persistent Homology (PH) technique.
 The purposes are:
7
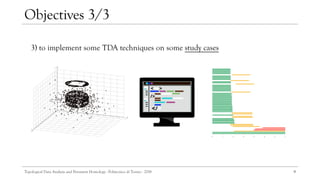
Objectives 1/3
1) to provide a satisfying explanation of TDA and PH fundamentals
[2]

8
Objectives 2/3
2) to analyze the robustness and the reliability of the inferred features
[3]

9
Objectives 3/3
3) to implement some TDA techniques on some study cases

 The input is a finite set of elements coming with a notion of distance
between them.
 The elements are mapped into a point cloud (PCD).
 PCD is completed by building "continuous" shape, a complex, on it.
10
From PCD to Complex
[13]
A
B
C
B
A
C
A
B
C

 There are many ways to build simplicial complexes from a topological space.
 To be a useful, a simplicial complex has to have an homology that approximates the
one of the space we want to study.
11
[18]
Simplicial Complexes

12
Cech and Vietoris–Rips Complexes
 Reconstruction Theorem
 Nerve Theorem
 𝐶 𝛼(X) ⊂ 𝑉2𝛼(X) ⊂ 𝐶2𝛼(X)
Cech complex is difficult to calculate, but it is quite small
and accurate.
[19]
𝐶 𝛼 𝑋 ≔ 𝑝1, … , 𝑝k : 𝑝1, … , 𝑝k ⊂ 𝑋,∩𝑖 𝐵 𝛼 𝑝i ≠ ∅
𝑉𝛼 𝑋 ≔ 𝑝1, … , 𝑝k : 𝑝1, … , 𝑝k ⊂ 𝑋, 𝑚𝑎𝑥 𝑝i,𝑝j∈𝜎
(𝑑(𝑝i, 𝑝j)) ≤ 𝛼
Vietoris–Rips complex is easy to calculate, but it is usually very
big and less accurate.

 The homotopy equivalent items shares the same homology.
 Homology groups are a more computable alternative to homotopy ones.
13
Homology
Boundary Operator
𝜎 = [𝑣0, … , 𝑣 𝑘] 𝜕 𝑘 𝜎 = ෍
𝑖=0
𝑛
−1 𝑖
𝑣0,…, ො𝑣𝑖,…, 𝑣 𝑘
Simplex
𝜕 𝑣0, 𝑣1, 𝑣2, 𝑣3 = 𝑣1, 𝑣2, 𝑣3 - 𝑣0, 𝑣2, 𝑣3 + 𝑣0, 𝑣1, 𝑣3 - 𝑣0, 𝑣1, 𝑣2
[8]

14
Homology Groups
Cycles
𝑍 𝑘 = 𝐾𝑒𝑟(𝜕 𝑘)
Boundaries
𝐵 𝑘 = 𝐼𝑚(𝜕 𝑘+1)
k-th Homology Group
𝐻 𝑘 = 𝑍 𝑘/𝐵 𝑘
 The goal of homology is to discard cycles that are also boundaries, so we quotient
𝑍 𝑘 using the following equivalence relation
 The rank of 𝐻 𝑘 is 𝛽 𝑘.
𝛽0 = #Components 𝛽1 = #Loops 𝛽2 = #Voids 𝛽 𝑛 = # n-dim Holes
∀𝑧1, 𝑧2 ∈ 𝑍 𝑘, 𝑧1~𝑧2 ⇔ 𝑧1 − 𝑧2 ∈ 𝐵 𝑘

The sequence of simplicial complexes with its inclusion maps is a filtration.
[20]
15
Filtrations
Which 𝑑 should we choose?
The most persistent features are detected using PH. They are supposed to represent
true characteristics of the underlying space.

16
Persistent Homology
 With PH we study the homology of a filtration as a single algebraic entity.
 Its features can be then analyzed using its barcode representation and this is
formally justiﬁed by the Structure Theorem.
Definition
When 0 ≤ 𝑖 ≤ 𝑗 ≤ 𝑛, the inclusion 𝑥𝑖
𝑗
:𝑋𝑖 ↪ 𝑋𝑗 induces a homomorphism
𝐻(𝑥𝑖
𝑗
):𝐻(𝑋𝑖) → 𝐻(𝑋𝑗) whose images are the persistent homology groups.

17
Persistence Barcode
[21]

18
Persistence Diagram
 Persistence Diagram
 Given two persistent diagrams 𝐷1 and 𝐷2, the Bottleneck distance between them is
𝑑 𝐵 𝐷1, 𝐷2 = 𝑖𝑛𝑓𝛾 𝑠𝑢𝑝 𝑥∈𝐷1
| 𝑥 − 𝛾 𝑥 |∞ where 𝛾 ranges over all multi-bijections
𝐷1 → 𝐷2 .
[23]

19
Stability Results
Theorem
Let 𝑋 and 𝑌 be two compact metric spaces and let 𝐹𝑖𝑙𝑡(𝑋)
and 𝐹𝑖𝑙𝑡(𝑌) be the Vietoris–Rips filtrations built on top them.
Then
𝑑 𝐵(𝐷(𝐹𝑖𝑙𝑡 𝑋 ), 𝐷(𝐹𝑖𝑙𝑡 𝑌 )) ≤ 2𝑑 𝐺𝐻(𝑋, 𝑌)
Moreover, if 𝑋 and 𝑌 are embedded in the same space then
𝑑 𝐵(𝐷(𝐹𝑖𝑙𝑡 𝑋 ), 𝐷(𝐹𝑖𝑙𝑡 𝑌 )) ≤ 2𝑑 𝐻(𝑋, 𝑌)
[24]

20
Statistical Results
The most persistent features can be detected and separated from topological
noise using statistical methods as the Bootstrap.
Given a persistence diagram 𝑋 with an estimator ෠𝑋, with look for 𝛿 𝛼 such that
𝑃 𝑑 𝐵 𝑋, ෠𝑋 ≥ 𝛿 𝛼 ≤α, α∈(0,1)
The confidence set will be 𝑋: 𝑑 𝐵 𝑋, ෠𝑋 ≥ 𝛿 𝛼
[25]

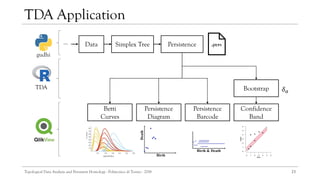
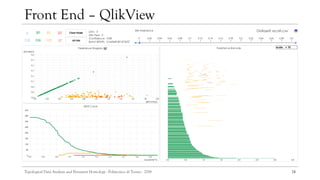
21
Implementation
[27]
 To analyze the topological information of different datasets, a console application
was implemented using GUDHI in Python, TDA in R and QlikView.
 GUDHI proposed an efficient tree representation for simplicial complexes, the
simplex tree.
+ +

22
Data Upload
Data
Upload
Consistency
Checks
Dimension
Plot
Data …
pandas
matplotlib

23
TDA Application
Data Simplex Tree Persistence
Persistence
Diagram
Persistence
Barcode
Bootstrap
.pers
gudhi
TDA
Confidence
Band
…
Betti
Curves
𝛿 𝛼

24
Front End – QlikView

25
Results

BIBLIOGRAPHY
[1] G. Carlsson, The Shape of Data conference, Ayasdi Energy Summit, 2014.
[2] R. Ghrist, Three examples of applied and computational homology, 2008.
[3] P.Bubenik, Statistical Topological Data Analysis using Persistence Landscapes, Journal of Machine Learning Research 16, 2015.
[4] M. Alagappan, J. Carlsson, G. Carlsson, T. Ishkanov, A. Lehman, P. Y. Lum, G. Singh, and M. Vejdemo-Johansson, Extracting insights from the shape of complex data using topology,
Scientific Reports v. 3, Article number: 1236, 2013.
[5] R. Carhart-Harris, P. Expert, P. J. Hellyer, D. Nutt, G. Petri, F. Turkheimer and F. Vaccarino, Homological scaffolds of brain functional networks, Journal of The Royal Society Interface,
11(101):20140873, 2014.
[6] M. Lesnick, Studying the Shape of Data Using Topology, Institute for Advanced Study, School of Mathematics, 2013.
[7] P. Chardy, V. David and B. Sautour, Fitting a predator–prey model to zooplankton time-series data in the Gironde estuary (France): Ecological significance of the parameters, Estuarine,
Coastal and Shelf Science, Volume 67, Issue 4, Pages 605-617, 2006.
[8] S. Maletic, M. Rajkovic and Y. Zhao, Persistent topological features of dynamical systems, doi.org/10.1063/1.4949472, 2016.
[9] X. Feng, Y. Tong, G. W. Wei and K. Xia, Topological modeling of biomolecular data, Nanyang Technological University.
[10] B.Cottenceau, N.Delanoue ,L.Jaulin, Guaranteeing the homotopy type of a set defined by non-linear inequalities, DOI: 10.1007/s11155-007-9043-8, 2006.
[11] P. Lambrechts, The Poincaré conjecture and the shape of the universe slides, Wellesley College, 2009.
[12] E.A.Coutsias,S.Martin,A.ThompsonandJ.P.Watson,Topologyofcyclo-octaneenergylandscape, doi: 10.1063/1.3445267, 2010.
[13] G. Carlsson, T. Ishkhanov , D. L. Ringac, F. Memoli, G. Sapiro and G. Singh, Topological analysis of population activity in visual cortex, Journal of vision 8 8 (2008): 11.1-18.
[14] A. Hatcher, Algebraic Topology, Cambridge University Press, ISBN 0-521-79540-0, 2002.
[15] E.G.P. P. Bos, M. Caroli, R. van de Weygaert, H. Edelsbrunner, B. Eldering, M. van Engelen, J. Feldbrugge, E. ten Have, W. A. Hellwing, J. Hidding, B. J. T. Jones, N. Kruithof, C. Park,
P. Pranav, M.Teillaud and G.Vegter, Alpha,Betti and the Megaparsec Universe: on the Topology of the Cosmic Web, arXiv:1306.3640v1 [astro-ph.CO], 2013.
[16] J Cisewski-Kehea, S.B.Greenb, D.Nagai and X.Xu,Finding cosmic voids and filament loops using topological data analysis, arXiv:1811.08450v1 [astro-ph.CO], 2018.
[17] H. Liang and H. Wang, Structure-Function Network Mapping and Its Assessment via Persistent Homology, doi:10.1371/journal.pcbi.1005325, 2017.
[18] K. G. Wang, The Basic Theory of Presisten Homology, 2012.
[19] F. Chazal and B. Michel, An introduction to Topological Data Analysis: fundamental and practical aspects for data scientists, arXiv:1710.04019v1 [math.ST], 2017.
[20] M. Wright, Introduction to Persistent Homology video on M. Wright channel https : //www.youtube.com/watch?v = 2PSqWBIrn90 consulted on 10/10/2018, 2016.
[21] R. Ghrist, Barcodes: The Persistent Topology Of Data, Bull. Amer. Math. Soc. 45 (2008), 61-75 , Doi: https://doi.org/10.1090/S0273-0979-07-01191-3, 2007.
[22] G. W. Wei and K. Xia, Persistent homology analysis of protein structure, flexibility and folding, arXiv:1412.2779v1 [q-bio.BM], 2014.
[23] The NIPS 2012 workshop on Algebraic Topology and Machine Learning.
[24] K.Fukumizu,Y.HiraokaandG.Kusano,PersistenceweightedGaussiankernelfortopologicaldata analysis, 2016.
[25] J.Cisewski-Kehea,S.B.Greenb,D.NagaiandX.Xu,Findingcosmicvoidsandfilamentloopsusing topological data analysis, arXiv:1811.08450v1 [astro-ph.CO], 2018.
[26] H. A. Harrington, M. A. Porter and B. J. Stolz, Persistent homology of time-dependent functional networks constructed from coupled time series, DOI:10.1063/1.4978997, 2017.
[27] J. Boissonnat, C. Maria, The Simplex Tree: An Efficient Data Structure for General Simplicial Complexes, [Research Report] RR-7993, pp.20. <hal-00707901v1>, 2012.

Topological Data Analysis and Persistent Homology

More Related Content

What's hot

Similar to Topological Data Analysis and Persistent Homology

Recently uploaded

Topological Data Analysis and Persistent Homology