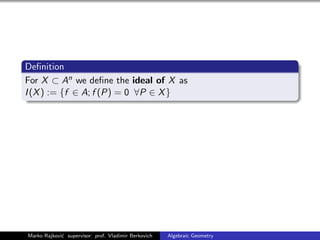
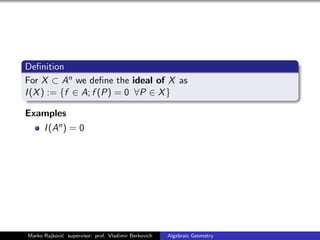
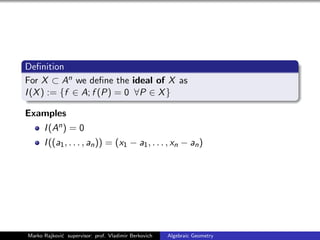
The document discusses the fundamentals of algebraic geometry. It introduces algebraic varieties as the zero sets of polynomial equations. The Zariski topology is defined, where closed sets are algebraic sets. Affine varieties are irreducible closed subsets of algebraic sets. Ideals of varieties are discussed, along with the correspondence between points and maximal ideals given by the Hilbert Nullstellensatz. Irreducible affine varieties are characterized by having prime ideals. The affine coordinate ring of a variety is introduced. Examples of algebraic sets and varieties in different dimensions are provided, including the twisted cubic curve.

1. Algebraic Geometry
Marko Rajkovi´c
supervisor: prof. Vladimir Berkovich
August 17, 2015
Marko Rajkovi´c supervisor: prof. Vladimir Berkovich Algebraic Geometry

2. Introduction
Studying systems of polynomial equations in several variables
and using abstract algebraic techniques for solving geometrical
problems about zeros of such systems
Marko Rajkovi´c supervisor: prof. Vladimir Berkovich Algebraic Geometry

3. Introduction
Studying systems of polynomial equations in several variables
and using abstract algebraic techniques for solving geometrical
problems about zeros of such systems
Establishing correspondences between geometric and algebraic
objects
Marko Rajkovi´c supervisor: prof. Vladimir Berkovich Algebraic Geometry

4. Introduction
Studying systems of polynomial equations in several variables
and using abstract algebraic techniques for solving geometrical
problems about zeros of such systems
Establishing correspondences between geometric and algebraic
objects
Fundamental objects of study are algebraic varieties
Marko Rajkovi´c supervisor: prof. Vladimir Berkovich Algebraic Geometry

5. Affine Varieties
Definition
For an algebraically closed field k affine n-space over k is set
An := {(a1, . . . an); ai ∈ k for 1 ≤ i ≤ n}.
Marko Rajkovi´c supervisor: prof. Vladimir Berkovich Algebraic Geometry

6. Affine Varieties
Definition
For an algebraically closed field k affine n-space over k is set
An := {(a1, . . . an); ai ∈ k for 1 ≤ i ≤ n}. For
S ⊂ A = k[x1, . . . , xn] we define the zero set of S as:
Z(S) := {P ∈ An; f (P) = 0 ∀f ∈ S}. Sets of this form are called
algebraic sets.
Marko Rajkovi´c supervisor: prof. Vladimir Berkovich Algebraic Geometry

7. Affine Varieties
Definition
For an algebraically closed field k affine n-space over k is set
An := {(a1, . . . an); ai ∈ k for 1 ≤ i ≤ n}. For
S ⊂ A = k[x1, . . . , xn] we define the zero set of S as:
Z(S) := {P ∈ An; f (P) = 0 ∀f ∈ S}. Sets of this form are called
algebraic sets.
Examples of algebraic sets
An = Z(0)
Marko Rajkovi´c supervisor: prof. Vladimir Berkovich Algebraic Geometry

8. Affine Varieties
Definition
For an algebraically closed field k affine n-space over k is set
An := {(a1, . . . an); ai ∈ k for 1 ≤ i ≤ n}. For
S ⊂ A = k[x1, . . . , xn] we define the zero set of S as:
Z(S) := {P ∈ An; f (P) = 0 ∀f ∈ S}. Sets of this form are called
algebraic sets.
Examples of algebraic sets
An = Z(0)
∅ = Z(1)
Marko Rajkovi´c supervisor: prof. Vladimir Berkovich Algebraic Geometry

9. Affine Varieties
Definition
For an algebraically closed field k affine n-space over k is set
An := {(a1, . . . an); ai ∈ k for 1 ≤ i ≤ n}. For
S ⊂ A = k[x1, . . . , xn] we define the zero set of S as:
Z(S) := {P ∈ An; f (P) = 0 ∀f ∈ S}. Sets of this form are called
algebraic sets.
Examples of algebraic sets
An = Z(0)
∅ = Z(1)
(a1, . . . , an) = Z(x1 − a1, . . . , xn − an)
Marko Rajkovi´c supervisor: prof. Vladimir Berkovich Algebraic Geometry

10. Affine Varieties
Definition
For an algebraically closed field k affine n-space over k is set
An := {(a1, . . . an); ai ∈ k for 1 ≤ i ≤ n}. For
S ⊂ A = k[x1, . . . , xn] we define the zero set of S as:
Z(S) := {P ∈ An; f (P) = 0 ∀f ∈ S}. Sets of this form are called
algebraic sets.
Examples of algebraic sets
An = Z(0)
∅ = Z(1)
(a1, . . . , an) = Z(x1 − a1, . . . , xn − an)
Arbitrary intersections and finite unions of algebraic sets are again
algebraic sets.
Marko Rajkovi´c supervisor: prof. Vladimir Berkovich Algebraic Geometry

11. Definition
Zariski topology on An is the topology whose closed sets are the
algebraic sets. Any subset X of An will be equipped with the
topology induced by the Zariski topology on An. This is called the
Zariski topology on X.
Marko Rajkovi´c supervisor: prof. Vladimir Berkovich Algebraic Geometry

12. Definition
Zariski topology on An is the topology whose closed sets are the
algebraic sets. Any subset X of An will be equipped with the
topology induced by the Zariski topology on An. This is called the
Zariski topology on X.
Example
Algebraic (closed) sets in A1 are finite subsets (including empty
set) as sets of zeros of single non-zero polynomial and whole set
(corresponding to zero polynomial).
Marko Rajkovi´c supervisor: prof. Vladimir Berkovich Algebraic Geometry

13. Definition
A non-empty subset Y of topological space X is called irreducible
if it is not a union of two proper closed subsets.
An (irreducible) affine variety is an (irreducible) closed subset of
An with Zariski topology.
Marko Rajkovi´c supervisor: prof. Vladimir Berkovich Algebraic Geometry

14. Definition
A non-empty subset Y of topological space X is called irreducible
if it is not a union of two proper closed subsets.
An (irreducible) affine variety is an (irreducible) closed subset of
An with Zariski topology.
Example
A1 is an irreducible affine variety since its only proper closed
subsets are finite and it is infinite. Generally, An is an irreducible
affine variety for every integer n.
Marko Rajkovi´c supervisor: prof. Vladimir Berkovich Algebraic Geometry

15. Definition
For X ⊂ An we define the ideal of X as
I(X) := {f ∈ A; f (P) = 0 ∀P ∈ X}
Marko Rajkovi´c supervisor: prof. Vladimir Berkovich Algebraic Geometry

16. Definition
For X ⊂ An we define the ideal of X as
I(X) := {f ∈ A; f (P) = 0 ∀P ∈ X}
Examples
I(An) = 0
Marko Rajkovi´c supervisor: prof. Vladimir Berkovich Algebraic Geometry

17. Definition
For X ⊂ An we define the ideal of X as
I(X) := {f ∈ A; f (P) = 0 ∀P ∈ X}
Examples
I(An) = 0
I((a1, . . . , an)) = (x1 − a1, . . . , xn − an)
Marko Rajkovi´c supervisor: prof. Vladimir Berkovich Algebraic Geometry

18. Theorem–Hilbert Nullstelensatz
For algebraically closed field k maximal ideals of k[x1, . . . , xn] are
exactly the ideals of the form (x1 − a1, . . . , xn − an) for some
ai ∈ k.
Marko Rajkovi´c supervisor: prof. Vladimir Berkovich Algebraic Geometry

19. Theorem–Hilbert Nullstelensatz
For algebraically closed field k maximal ideals of k[x1, . . . , xn] are
exactly the ideals of the form (x1 − a1, . . . , xn − an) for some
ai ∈ k.
Corollary
There is a 1 : 1 correspondence
{points in An} ↔ {maximal ideals of k[x1, . . . , xn]}
given by
(a1, . . . , an) ↔ (x1 − a1, . . . , xn − an).
Marko Rajkovi´c supervisor: prof. Vladimir Berkovich Algebraic Geometry

20. Lemma and Definition
An algebraic set X ⊂ An is an irreducible affine variety if and only
if its ideal I(X) ⊂ A = k[x1, . . . , xn] is a prime ideal.
Marko Rajkovi´c supervisor: prof. Vladimir Berkovich Algebraic Geometry

21. Lemma and Definition
An algebraic set X ⊂ An is an irreducible affine variety if and only
if its ideal I(X) ⊂ A = k[x1, . . . , xn] is a prime ideal. We call
A(Y ) := A/I(Y ) affine coordinate ring of Y .
Marko Rajkovi´c supervisor: prof. Vladimir Berkovich Algebraic Geometry

22. Lemma and Definition
An algebraic set X ⊂ An is an irreducible affine variety if and only
if its ideal I(X) ⊂ A = k[x1, . . . , xn] is a prime ideal. We call
A(Y ) := A/I(Y ) affine coordinate ring of Y .
Examples
An is irreducible since its ideal is zero ideal which is prime.
Marko Rajkovi´c supervisor: prof. Vladimir Berkovich Algebraic Geometry

23. Lemma and Definition
An algebraic set X ⊂ An is an irreducible affine variety if and only
if its ideal I(X) ⊂ A = k[x1, . . . , xn] is a prime ideal. We call
A(Y ) := A/I(Y ) affine coordinate ring of Y .
Examples
An is irreducible since its ideal is zero ideal which is prime.
If f is irreducible polynomial in A = k[x1, . . . , xn] we get an
irreducible affine variety Y = Z(f ). For n = 2 we call it affine
curve of degree d, where d is degree of f. For n = 3 we have
surface and for n > 3 hypersurface.
Marko Rajkovi´c supervisor: prof. Vladimir Berkovich Algebraic Geometry

24. The Twisted Cubic Curve
Let Y = {(t, t2, t3); t ∈ k}. Then I(Y ) = (x2 − y, x3 − z) in
A = k[x, y, z].
A/I(Y ) = k[x, y, z]/(x2
− y, x3
− z) ∼= k[x, x2
, x3
] ∼= k[t]
which is an integral domain. Hence, I(Y ) is prime ideal and Y is
an affine variety.
Marko Rajkovi´c supervisor: prof. Vladimir Berkovich Algebraic Geometry

25. THANK YOU FOR YOUR
ATTENTION!
Marko Rajkovi´c supervisor: prof. Vladimir Berkovich Algebraic Geometry