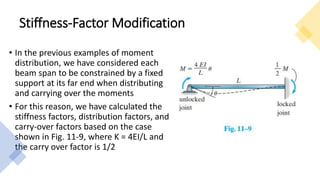
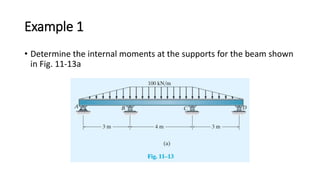
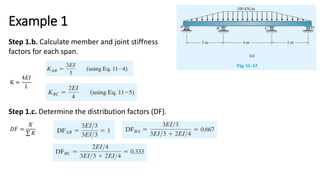
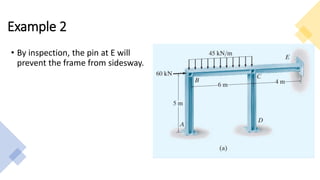
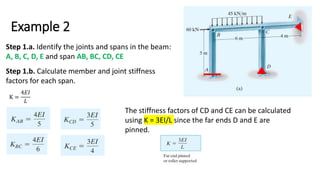
The document covers the stiffness-factor modification in moment distribution analysis for beams and frames under various support conditions, emphasizing cases like pin-supported beams and symmetric loading. It explains how to adjust stiffness factors to simplify calculations and uses examples to demonstrate the analysis process. Additionally, it provides guidance on applying the moment distribution method for frames without sidesway, detailing steps to calculate member and joint stiffness factors and distribution factors.

1. CED 426
Structural Theory II
Lecture 18
Moment Distribution:
Stiffness-Factor Modification and Frames no Sideways
Mary Joanne C. Aniñon
Instructor

2. Stiffness-Factor Modification
• In the previous examples of moment
distribution, we have considered each
beam span to be constrained by a fixed
support at its far end when distributing
and carrying over the moments
• For this reason, we have calculated the
stiffness factors, distribution factors, and
carry-over factors based on the case
shown in Fig. 11-9, where K = 4EI/L and
the carry over factor is 1/2

3. Stiffness-Factor Modification
• In some cases, it is possible to modify the stiffness factor of a span
and thereby simplify the process of moment distribution.
• Three cases where this frequently occurs will be considered:
a) Member Pin Supported at Far End
b) Symmetric Beam and Loading
c) Symmetric Beam with Antisymmetric loading

4. • Many beams are supported at their ends by a
pin (or roller) as shown in Fig. 11–10a.
• We can determine the stiffness factor at joint
A of this beam by applying a moment M at the
joint and relating it to the angle 𝜃 . To do this
we must find the shear in the conjugate beam
at A’
Member Pin Supported at Far End

5. • From the conjugate beam Fig. 11-10b, we have
Member Pin Supported at Far End

6. • Also, note that the carry-over factor is zero since
the pin at B does not support a moment.
• By comparison, then, if the far end were fixed
supported, the stiffness factor K = 4EI/L would
have to be modified by 3/4 to model the case of
having the far end pin supported.
Member Pin Supported at Far End

7. Symmetric Beam and Loading
• If a beam is symmetric with respect to both its loading and geometry,
the bending moment diagram for the beam will also be symmetric.
• As a result, a modification of the stiffness factor for the center span
can be made, so that moments in the beam only have to be
distributed through a joint lying on either half of the beam.

8. Symmetric Beam and Loading
• To develop the appropriate stiffness-factor modification, consider the
beam shown in Fig.11-11a. Due to the symmetry, the internal
moments at B and C are equal. Assuming this value to be M, the
conjugate beam for span BC is shown in Fig.11-11b

9. Symmetric Beam and Loading

10. Symmetric Beam with Antisymmetric loading
• If the asymmetric beam is subjected to antisymmetric loading, the
resulting moment diagram will be antisymmetric.
• Considering the beam Fig. 11-12a, due to the antisymmetric loading, the
internal moment at B is equal but opposite to that of C
• Assuming the value to be M, the conjugate beam for its center span BC is
shown in Fig. 11-12b.

11. Symmetric Beam with Antisymmetric loading

12. Example 1
• Determine the internal moments at the supports for the beam shown
in Fig. 11-13a

13. Example 1
Step 1.a. Identify the joints and spans in the
beam: A, B, C, D and span AB, BC, CD
Step 1.b. Calculate member and joint stiffness
factors for each span.
• By inspection, the beam and loading are symmetrical
• We will apply K=2EI/L to calculate the stiffness factor of the center span BC and therefore
use only the left half of the beam for analysis.
• The analysis can be shortened even further by using K = 3EI/L for calculating the stiffness of
segment AB since the far end A is pinned.

14. Example 1
Step 1.b. Calculate member and joint stiffness
factors for each span.
Step 1.c. Determine the distribution factors (DF).
K =
4𝐸𝐼
𝐿
𝐷𝐹 =
𝐾
𝐾

15. Example 1
1.d. Determine the fixed-end moments
FEMBA
FEMAB =0 FEMBC FEMCB
FEMCD FEMDC =0

16. Example 1
FEMBA
FEMAB =0 FEMBC FEMCB
FEMCD FEMDC =0
Joint A B
Member AB BA BC
DF 1 0.667 0.333
FEM
Dist.
0
0
60
48.9
-133.33
24.4
∑M 0 108.9 -108.9
• The data are listed in the table.
• Calculating the stiffness factors as
shown considerably reduces the
analysis, since only joint B must be
balanced and carry-overs to joint A
and C are not necessary.

17. Moment Distribution For Frames: No Sidesway
• Application of the moment distribution method for frames having no
sideways follows the same procedure as that given for beams.
• To minimize the chance for errors, it is suggested that the analysis be
arranged in a tabular form, as in the previous examples
• The distribution of moments can be shortened if the stiffness factor of a
span can be modified.

18. Example 2
• Determine the internal moments at the joints of the frame shown in Fig.
11-15a. There is a pin at E and D and a fixed support at A. EI is constant

19. • By inspection, the pin at E will
prevent the frame from sidesway.
Example 2

20. Example 2
Step 1.a. Identify the joints and spans in the beam:
A, B, C, D, E and span AB, BC, CD, CE
Step 1.b. Calculate member and joint stiffness
factors for each span.
The stiffness factors of CD and CE can be calculated
using K = 3EI/L since the far ends D and E are
pinned.
K =
4𝐸𝐼
𝐿

21. Example 2
Step 1.c. Determine the distribution factors (DF).
𝐷𝐹 =
𝐾
𝐾
𝐷𝐹𝐵𝐶 =
4𝐸𝐼/6
4𝐸𝐼
5
+
4𝐸𝐼
6
= 0.455

22. Example 2
1.d. Determine the fixed-end moments

23. Example 2
Joint A B C D E
Member AB BA BC CB CE CD DC EC
DF 0 0.545 0.455 0.330 0.372 0.298 1 1
FEM
Dist.
0
0
0
73.6
-135
61.4
135
-44.6
0
-50.2
0
-40.2
0
0
0
0
CO
Dist.
36.8
0
0
12.2
-22.3
10.1
30.7
-10.1
0
-11.5
0
-9.1
0
0
0
0
CO
Dist.
6.1
0
0
2.8
-5.1
2.3
5.1
-1.7
0
-1.9
0
-1.5
0
0
0
0
CO
Dist.
1.4
0
0
0.4
-0.8
0.4
1.2
-0.4
0
-0.4
0
-0.4
0
0
0
0
CO
Dist.
0.2
0
0
0.1
-0.2
0.1
0.2
-0.1
0
-0.1
0
0
0
0
0
0
∑M 44.5 89.1 -89.1 115 -64.1 -51.2 0 0

24. Moment Diagram for frame
+
-
-
+