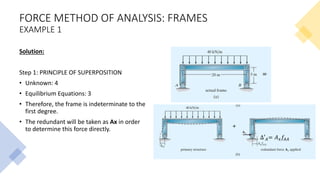
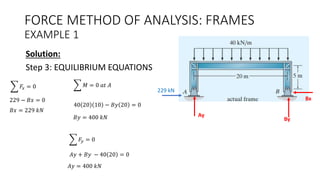
The document discusses the analysis of statically indeterminate structures using the force method, detailing requirements for equilibrium, compatibility, and force-displacement. It provides a systematic procedure for determining reactions and redundant forces by applying principles such as compatibility equations and virtual work. Examples illustrate how to solve for unknown forces and moments in frames using this method.

1. CED 426
Structural Theory II
Lecture 7
Force Method of Analysis: Frames
Mary Joanne C. Aniñon
Instructor

2. STATICALLY INDETERMINATE STUCTURES
• When all the on the stable structure can be determined strictly from
the equilibrium equations, the structure is referred to as statically
determinate.
• Structures having more unknown forces than available equilibrium
equations are called statically indeterminate.
• A structure is classified as statically indeterminate when the number
of unknowns exceed the number of equilibrium equations needed to
determine these unknowns.

3. METHOD OF ANALYSIS
• When analyzing any statically indeterminate structure, it is necessary
to satisfy the equilibrium, compatibility, and force-displacement
requirements for the structure.

4. METHOD OF ANALYSIS
• Equilibrium is satisfied when the reactive forces hold the structure at
rest.
• Compatibility is satisfied when the various segments of the structure
fit together without intentional breaks or overlaps.
• The force-displacement requirements depend upon the wat the
structure’s material responds to load. In this book (lecture), we have
assumed this to be a linear elastic response.

5. METHOD OF ANALYSIS
• In general, there are 2 different ways to satisfy these three
requirements.
• Force or Flexibility Method
• Displacement or Stiffness Method

6. METHOD OF ANALYSIS
• FORCE METHOD
• Originally developed by James Clerk Maxwell in 1864 and later refined by
Otto Mohr and Heinrich Muller-Breslau
• Since this method was based on compatibility forms, it has sometimes been
referred to as the compatibility method or the method of consistent
displacement.
• It consists of first writing equations that satisfy the compatibility and force-
displacement requirements for the structure in order to determine the
redundant forces.
• Then once these forces have been determined, the remaining reactive
forces on the structure are determined by satisfying the equilibrium
requirements.

7. PROCEDURE FOR ANALYSIS
• The following procedure provides a general method for determining the reactions of statically
indeterminate structures using the force or flexibility method of analysis.
1.a. Determine the unknown redundant forces.
1.b. Determine the equilibrium equations
1.c. Determine the number of degrees to which the
structure is indeterminate.
1.d. Specify the redundant forces/moments that
must be removed from the structure in order to
make it statically determinate and stable.
1.e. Draw the statically indeterminate structure and
show it equal to a series of corresponding statically
determinate structures.
1.f. Sketch the elastic curve on each structure and
indicate symbolically the displacement or rotation
at the point of each redundant force or moment.

8. PROCEDURE FOR ANALYSIS
• The following procedure provides a general method for determining the reactions of statically
indeterminate structures using the force or flexibility method of analysis.
2.a. Write the compatibility equation for the
displacement or rotation.
2.b. Determine all the deflections and flexibility
coefficients.
2.c. Substitute these results into the compatibility
equations.
2.d. Solve for the unknown redundant.

9. PROCEDURE FOR ANALYSIS
• The following procedure provides a general method for determining the reactions of statically
indeterminate structures using the force or flexibility method of analysis.

10. FORCE METHOD OF ANALYSIS: FRAMES
EXAMPLE 1
Problem

11. FORCE METHOD OF ANALYSIS: FRAMES
EXAMPLE 1
Solution:
Step 1: PRINCIPLE OF SUPERPOSITION
• Unknown: 4
• Equilibrium Equations: 3
• Therefore, the frame is indeterminate to the
first degree.
• The redundant will be taken as Ax in order
to determine this force directly.
∆′𝐴= 𝐴𝑥𝑓𝐴𝐴

12. FORCE METHOD OF ANALYSIS: FRAMES
EXAMPLE 1
Solution:
Step 2: COMPATIBILITY EQUATION
0 = ∆𝐴 + ∆′𝐴
∆′𝐴= 𝐴𝑥𝑓𝐴𝐴

13. FORCE METHOD OF ANALYSIS: FRAMES
EXAMPLE 1
Solution:
Determine the deflections and flexibility coefficient using
the method of virtual work:
• Assign 3 coordinates 𝑥1, 𝑥2, 𝑥3
• Remove the real loads, apply unit load (Ax = 1)
• Solve the reactions
𝐹𝑥 = 0
𝐴𝑥 − 𝐵𝑥 = 0
𝐵𝑥 = 1
𝐹𝑦 = 0
𝐴𝑦 = 𝐵𝑦 = 0

14. FORCE METHOD OF ANALYSIS: FRAMES
EXAMPLE 1
Solution:
• Solve the virtual moments, m
𝑀 = 0
𝑚1 − 1(𝑥1) = 0
𝑚1 = 1𝑥1
−𝑚2 − 1 5 = 0
𝑚2 = −5
−𝑚3 + 1(𝑥3) = 0
𝑚3 = 1𝑥3

15. FORCE METHOD OF ANALYSIS: FRAMES
EXAMPLE 1
Solution:
• Apply the real loads
• Solve the reactions
• Solve the real moments, M
𝑀 = 0
𝑀1 = 0 −𝑀2 − 40 𝑥2
𝑥2
2
+ 400(𝑥2) = 0 𝑀3 = 0
𝑀2 = 400𝑥2 − 20𝑥2
2
𝐹𝑥 = 0
𝐴𝑥 = 𝐵𝑥 = 0
𝑀𝐴 = 0
40 20 10 − 𝐵𝑦 20 = 0
𝐵𝑦 = 400
𝐹𝑦 = 0
𝐴𝑦 + 𝐵𝑦 − 40 10 = 0
𝐴𝑦 = 400

16. FORCE METHOD OF ANALYSIS: FRAMES
EXAMPLE 1
Solution:
• Virtual-Work Equation

17. FORCE METHOD OF ANALYSIS: FRAMES
EXAMPLE 1
Solution:
• Virtual-Work Equation
from Maxwell’s Theorem:
𝑓𝐴𝐴 =
(𝑚)(𝑚)
𝐸𝐼
𝑑𝑥

18. FORCE METHOD OF ANALYSIS: FRAMES
EXAMPLE 1
Solution:
• Substitute the results to the compatibility equation:

19. FORCE METHOD OF ANALYSIS: FRAMES
EXAMPLE 1
Solution:
Step 3: EQUILIBRIUM EQUATIONS
𝐹𝑥 = 0
229 − 𝐵𝑥 = 0
𝑀 = 0 𝑎𝑡 𝐴
40 20 10 − 𝐵𝑦 20 = 0
229 kN
Ay
Bx
By
𝐵𝑥 = 229 𝑘𝑁
𝐵𝑦 = 400 𝑘𝑁
𝐹𝑦 = 0
𝐴𝑦 + 𝐵𝑦 − 40 20 = 0
𝐴𝑦 = 400 𝑘𝑁