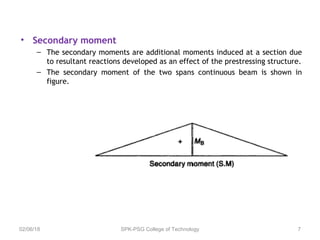
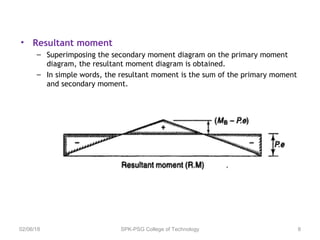
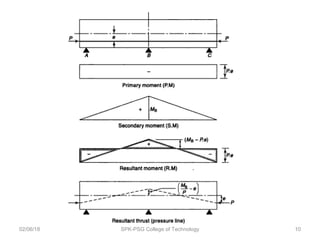
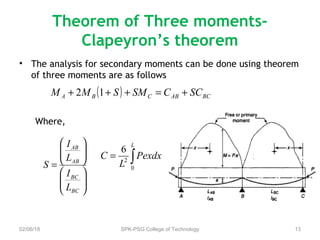
A continuous beam has more than one span carried by multiple supports. It is commonly used in bridge construction since simple beams cannot support large spans without requiring greater strength and stiffness. Continuous prestressed concrete beams provide adequate strength and stiffness while allowing for redistribution of moments, resulting in higher load capacity, reduced deflections, and more evenly distributed bending moments compared to equivalent simple beams. Analysis of continuous beams requires determining primary moments from prestressing, secondary moments induced by support reactions, and the combined resultant moments.

1. Continuous Beam

2. 02/06/18 SPK-PSG College of Technology 2
• A continuous beam is having more than one span is carried by
several supports.
• It is mainly used in bridge construction.
• Simple beam cannot be used for large spans, as it requires
more strength and stiffness.
• But continuous PSC beam not only provides adequate strength
and stiffness, but also provides sufficient ductility.
• An important distinction between them is that the prestressing
force does not produce any secondary moments in simple
beams, considerable secondary moments are produced in
continuous PSC beams.
• Also, the behavior of continuous PSC beams nearer to ultimate
load is different from the behavior of a corresponding simple
beam.
Continuous beam

3. Merits & demerits…
• Ultimate loads carrying capacity is higher than the statically
determinate structures due to the effect of redistribution of
moments.
• An increase in stability of framed structures. This is feasible
due to the distribution of moments.
• The deflections in continuous beams are relatively small when
compared to simply supported beams. This is due to the fact
that the continuity of members makes the rotation less at the
places of supports. Thus, the deflections are less.
• The maximum bending moment that occurs in a continuous
beam is less than that for same spans, if the beams are cut into
simply supported beams.
• In continuous beam, the bending moments are evenly
distributed throughout the span and results in reduction in size
of members. Thus, lighter weight structures made.
02/06/18 SPK-PSG College of Technology 3

4. • An effective usage of curved cables is possible to resist the
supports and span moments.
• A reduction in cost and construction time is possible due to the
use of number of anchorages.
Demerits
• Frictional loss in continuous tendons
• Shortening of long continuous beams under prestress
• Secondary stresses
• Location of both maximum moment and shear force over
supports
• Reversal of moments
• Moment packs
• Continuity for precast elements
• Difficulty in designing.
02/06/18 SPK-PSG College of Technology 4

5. Methods of achieving continuity
02/06/18 SPK-PSG College of Technology 5
To develop continuity between two
Precast beams by using cap cables
Continuity in PCC is achieved by using
curved or straight cables which are
Continuous over several spans
Straight tendons may be used over
the supports to develop continuity

6. Basic Definitions
• Primary moment
– Consider a two span continuous beam as shown in figure.
– The prestressing force is acting at an eccentricity, e though a straight
tendon. A hogging moment –Pe develops.
– This is termed as primary moment.
– The negative sign indicates the moment developed is hogging in nature,
02/06/18 SPK-PSG College of Technology 6

7. • Secondary moment
– The secondary moments are additional moments induced at a section due
to resultant reactions developed as an effect of the prestressing structure.
– The secondary moment of the two spans continuous beam is shown in
figure.
02/06/18 SPK-PSG College of Technology 7

8. • Resultant moment
– Superimposing the secondary moment diagram on the primary moment
diagram, the resultant moment diagram is obtained.
– In simple words, the resultant moment is the sum of the primary moment
and secondary moment.
02/06/18 SPK-PSG College of Technology 8

9. • Pressure line or thrust line
– The line joining the locus of the resultant compression at various sections
of a prestressed concrete beam is called pressure line or thrust line.
– In continuous ABC shown A and C are simple support. Hence MA=MC=0.
– Therefore, the location of pressure line at A and C are –e. by substituting
the value of M as zero in the equation(M/P-e).
– At the intermediate support N, moment is not equal to zero. Hence at B
the location of pressure line is (M/P-e)
02/06/18 SPK-PSG College of Technology 9

10. 02/06/18 SPK-PSG College of Technology 10

11. • Transformation profile
– A transformation profile is any tendon profile consisting of straight lines
between the rigid supports and having zero eccentricity at simple end
supports.
– A tendon following such a profile will produce support reactions and
uniform longitudinal compression but no bending moments.
02/06/18 SPK-PSG College of Technology 11

12. Methods of analysis of secondary
moments
• Assumptions
• The effect of change in the length of members due to the prestressing
force and external loading is negligible.
• The cable friction is considered to be negligible so that the prestressing
force is constant at al points of the cable.
There are several methods for analyzing statically indeterminate prestressed
structures to compute the secondary moments that develop from the
prestressing the structure.
• Methods
• Three moment theorem
• Consistent deformation
• Tendon reaction
02/06/18 SPK-PSG College of Technology 12

13. Theorem of Three moments-
Clapeyron’s theorem
• The analysis for secondary moments can be done using theorem
of three moments are as follows
Where,
02/06/18 SPK-PSG College of Technology 13
( ) BCABCBA SCCSMSMM +=+++ 12












=
BC
BC
AB
AB
L
I
L
I
S
∫=
L
Pexdx
L
C
0
2
6

14. • The simplified equation has been derived considering two
adjacent spans only.
• If there is another span then one more equation is to be
formulated to obtain secondary moment. The resultant moment
is the algebraic sum of primary and secondary moment.
Where R,P, S represents Resultant, primary and secondary
moments.
• The line of pressure or thrust line can be obtained from the
following equations
Where Pe – effective prestressing force.
02/06/18 SPK-PSG College of Technology 14
SPR MMM +=






−=
e
R
p
P
M
e

15. References
• Prestressed concrete-K.U.Muthu, Azmi Ibrahim,
Maganti Janardhana and M.Vijayanad (Based on IS
1343-2012)
• Design of prestressed concrete structures- T.Y.Lin
and NED.H.Burns.
• Fundamentals of Prestressed Concrete –N.C.Sinha and
S.K.Roy
• Prestressed concrete –N.Rajagopalan
• Prestressed Concrete- N.Krishna Raju
• Reinforced concrete –Limit State Design-Ashok K Jain
• IS 1343-2012-Prestressed Concrete Code of Practice
02/06/18 SPK-PSG College of Technology 15

16. Thanks for listening-
All the best
02/06/18 SPK-PSG College of Technology 16