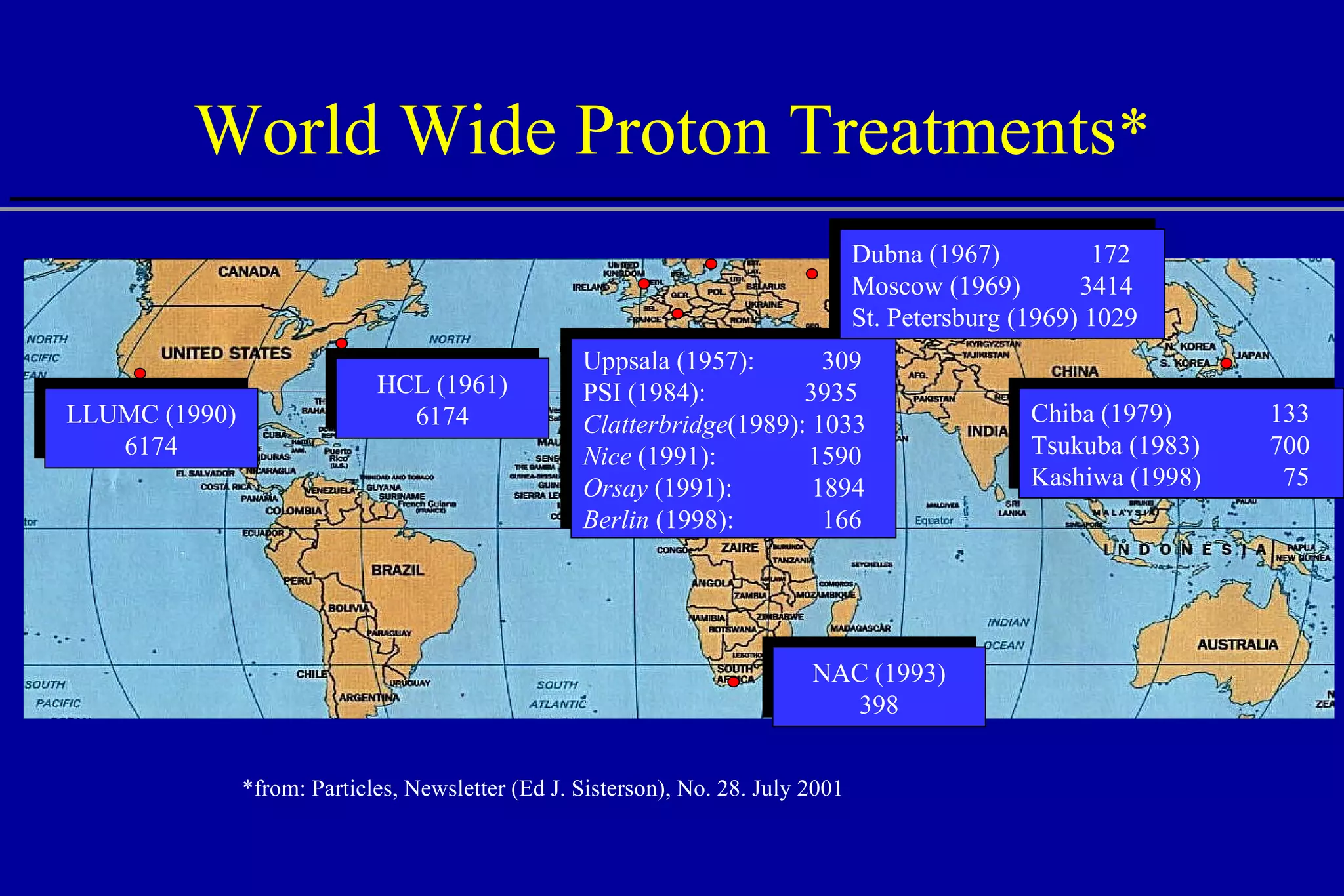
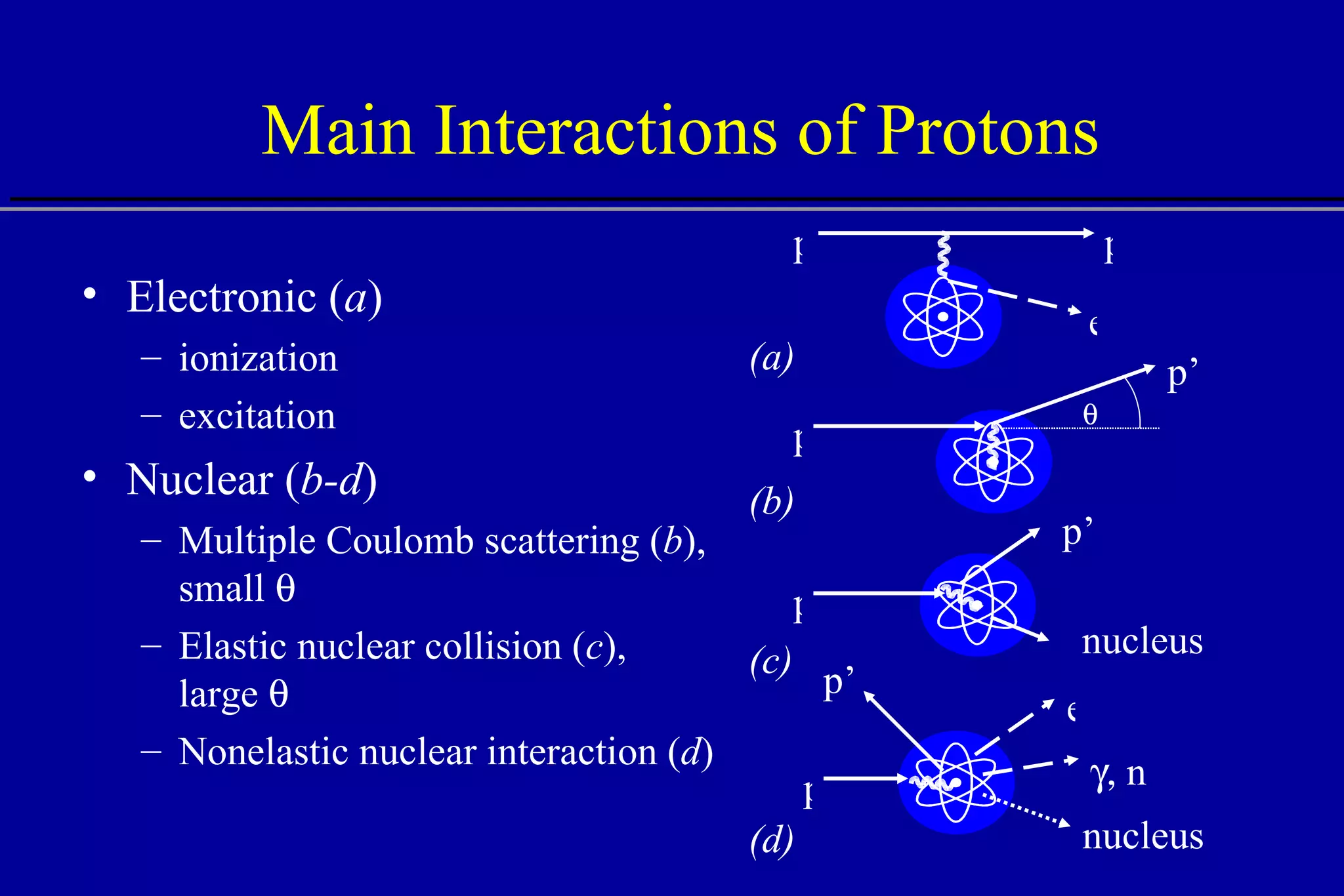
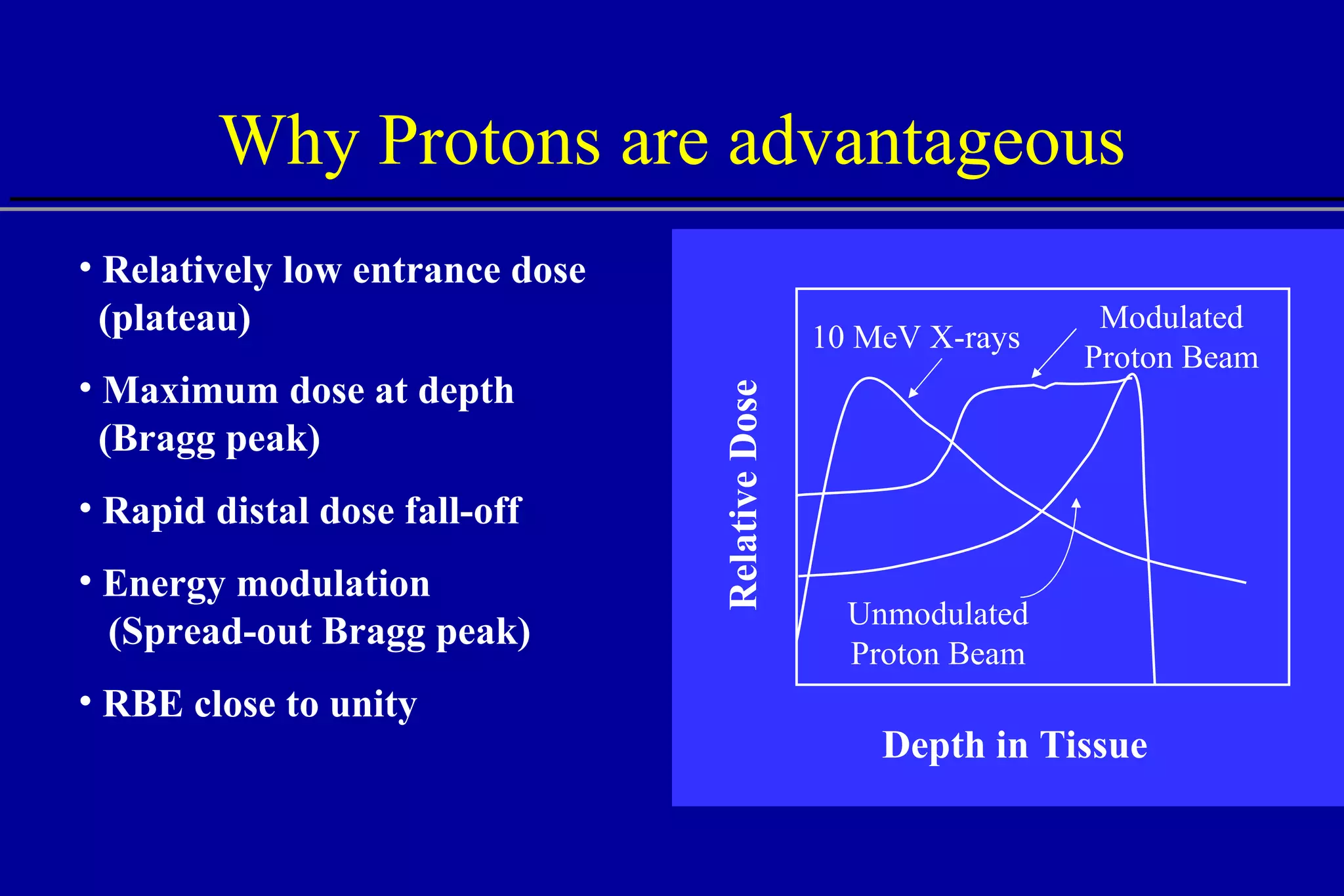
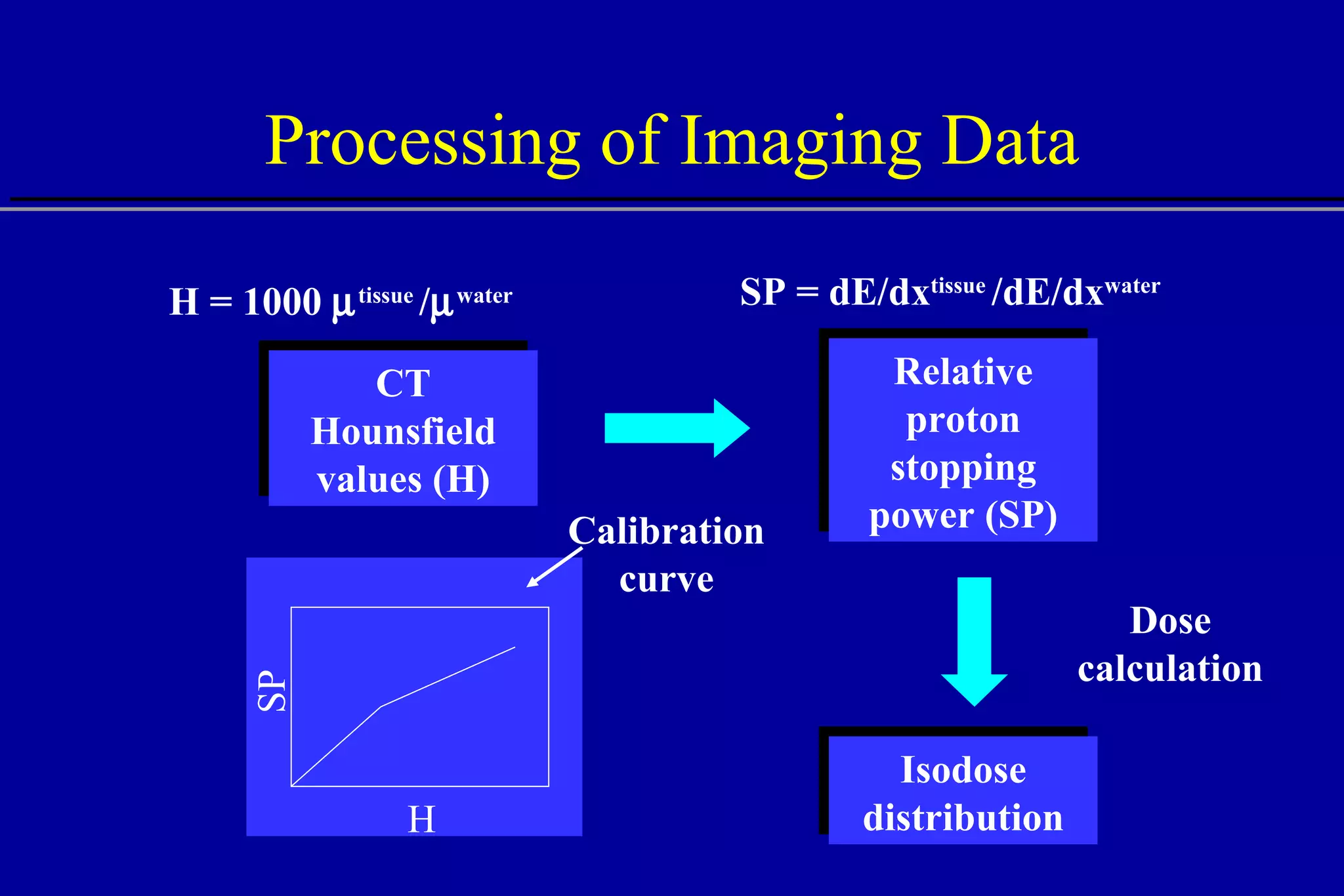
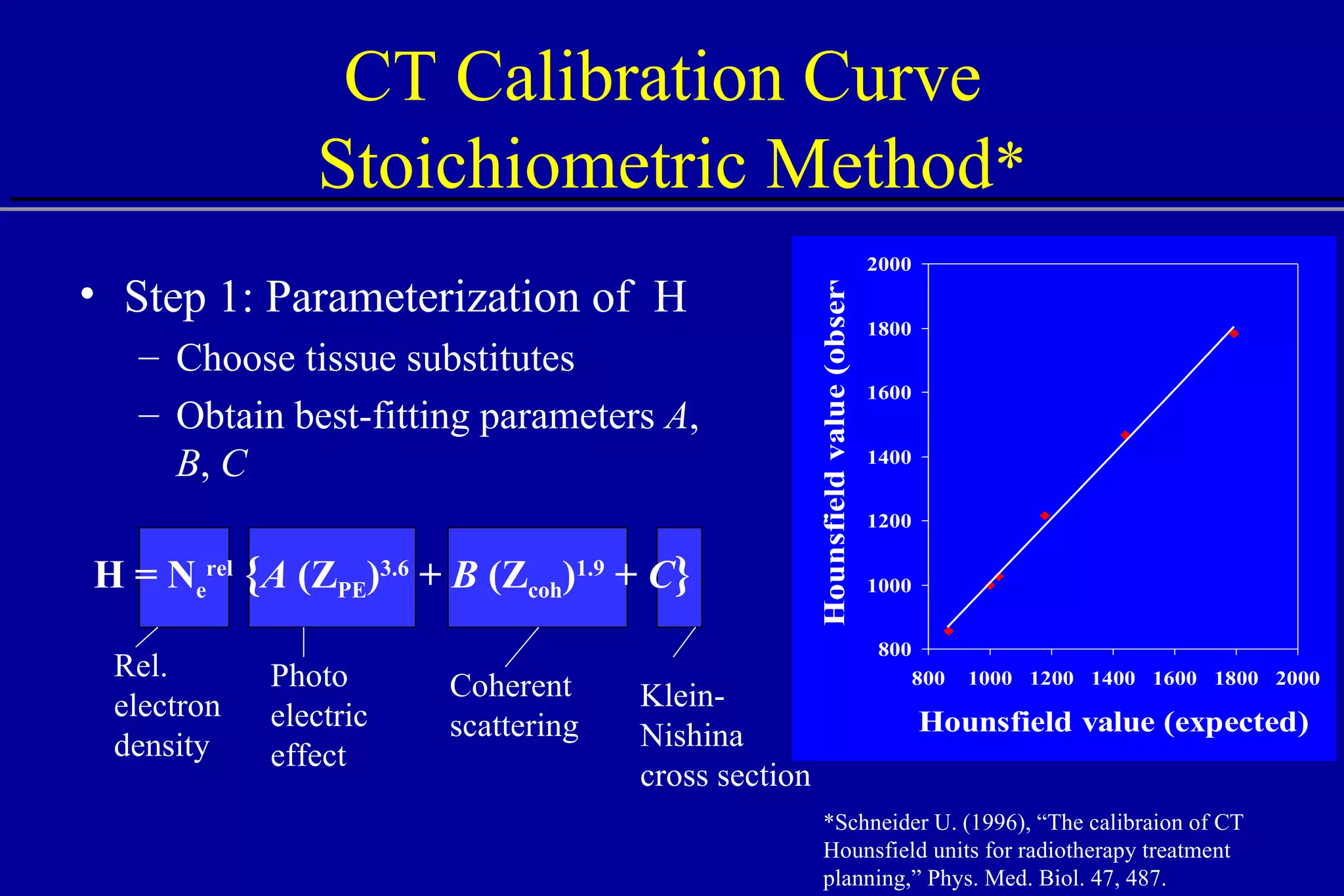
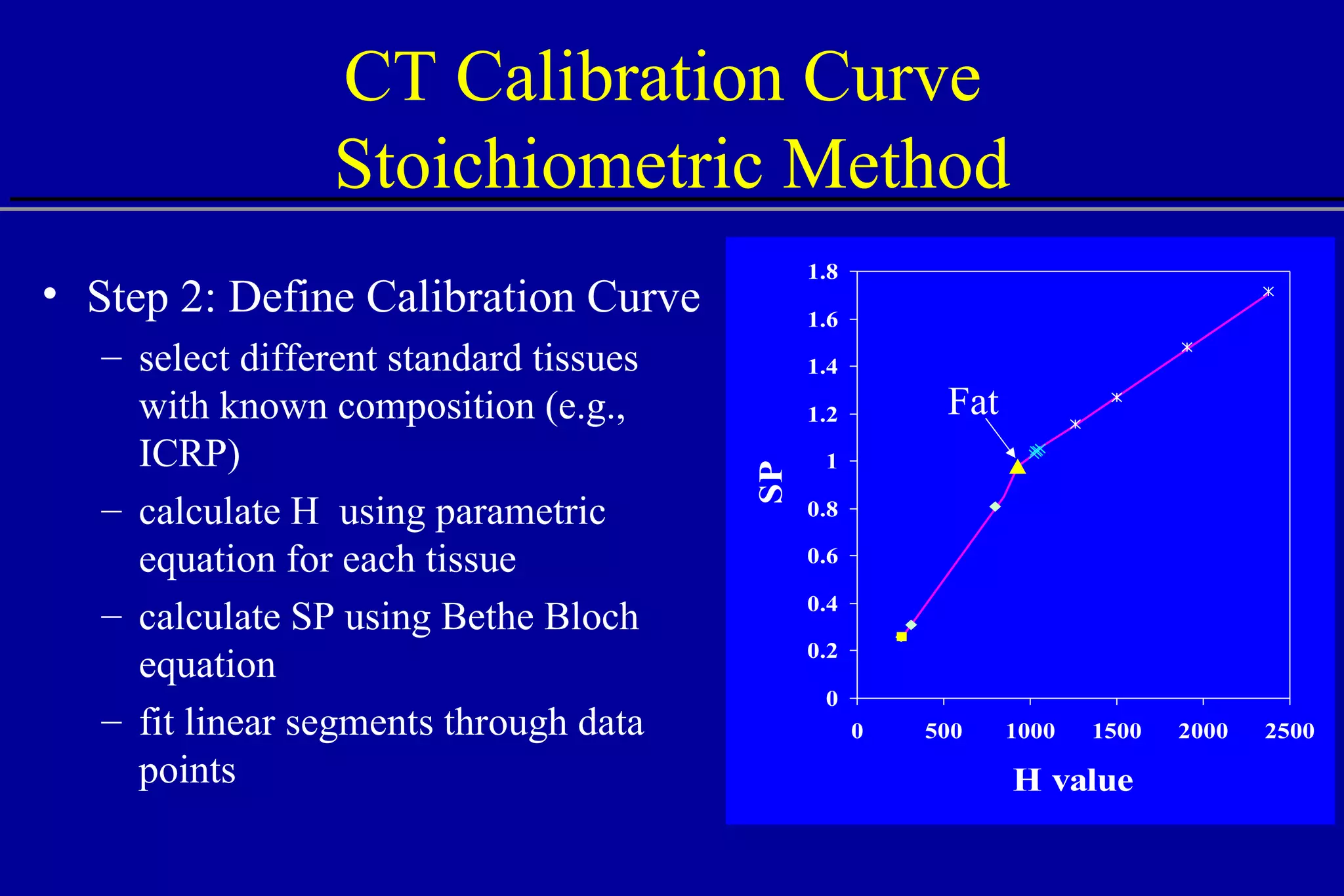
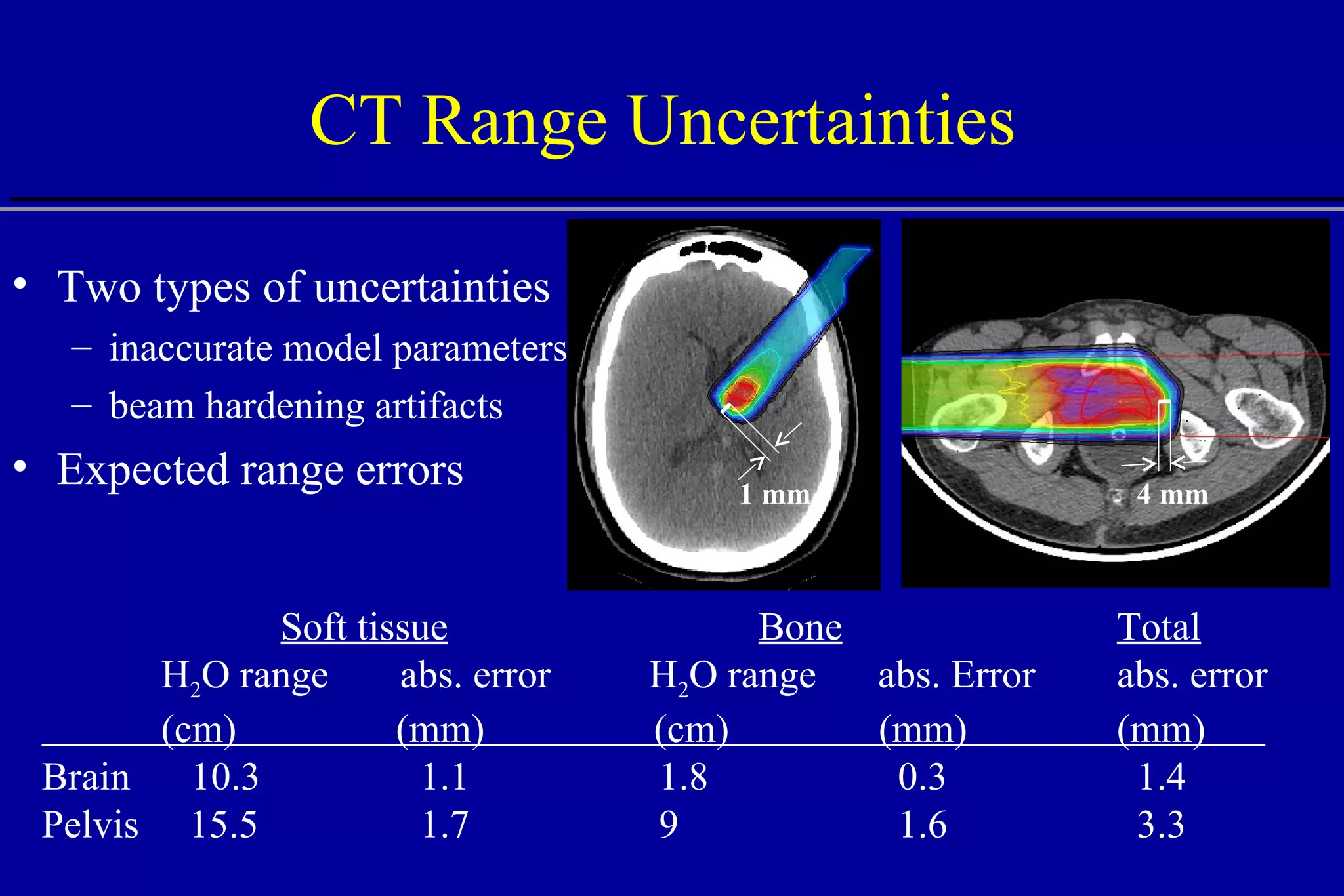
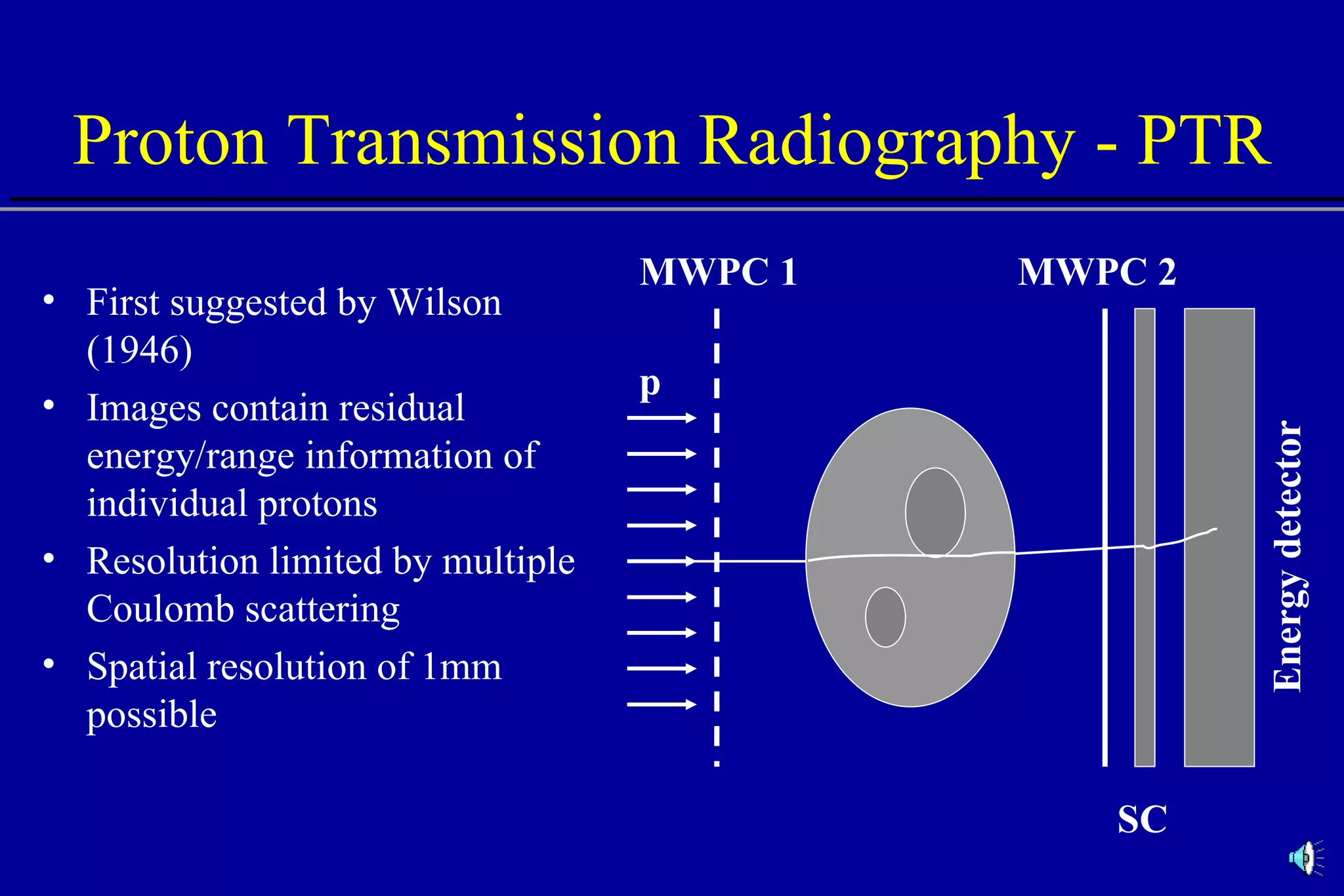
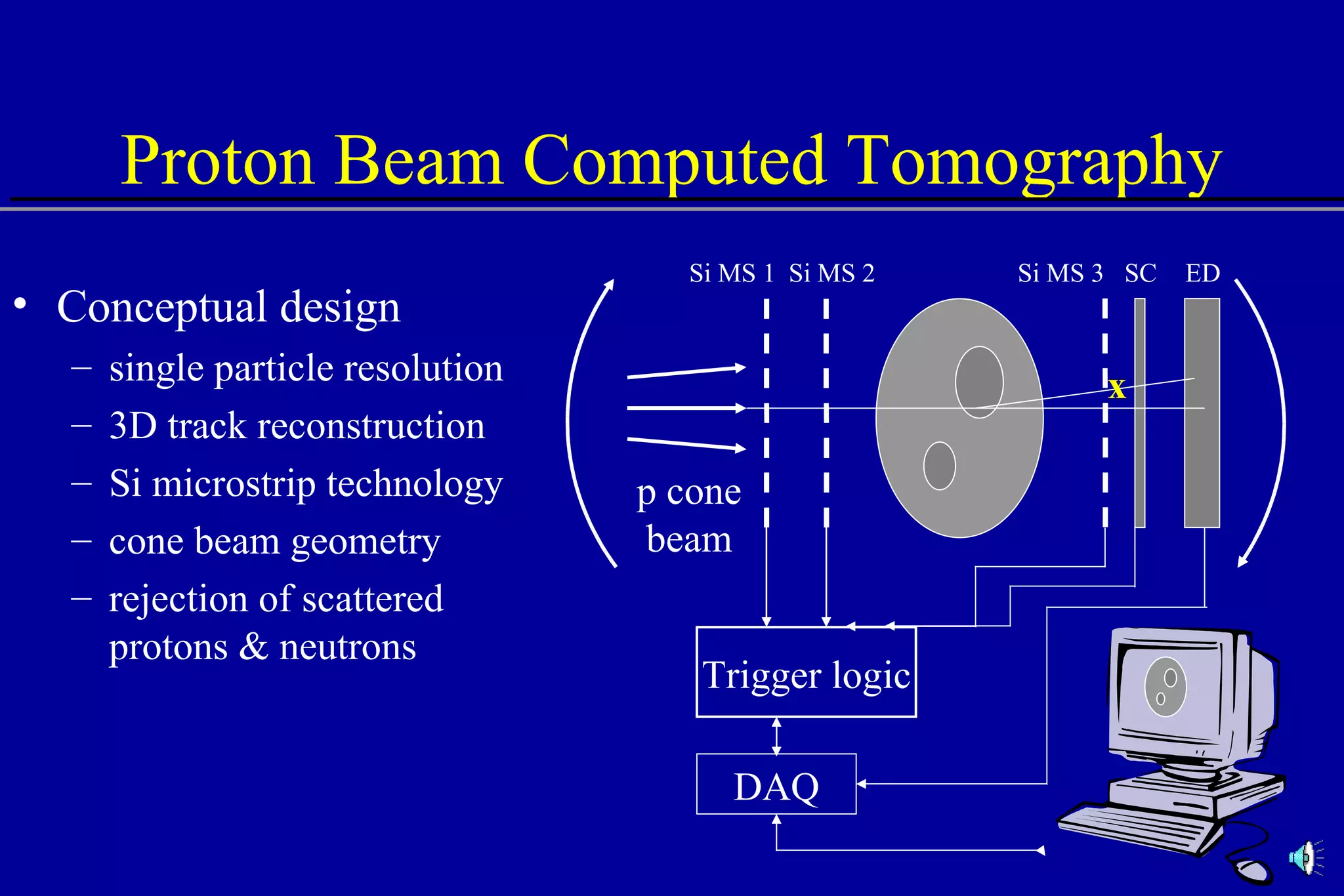
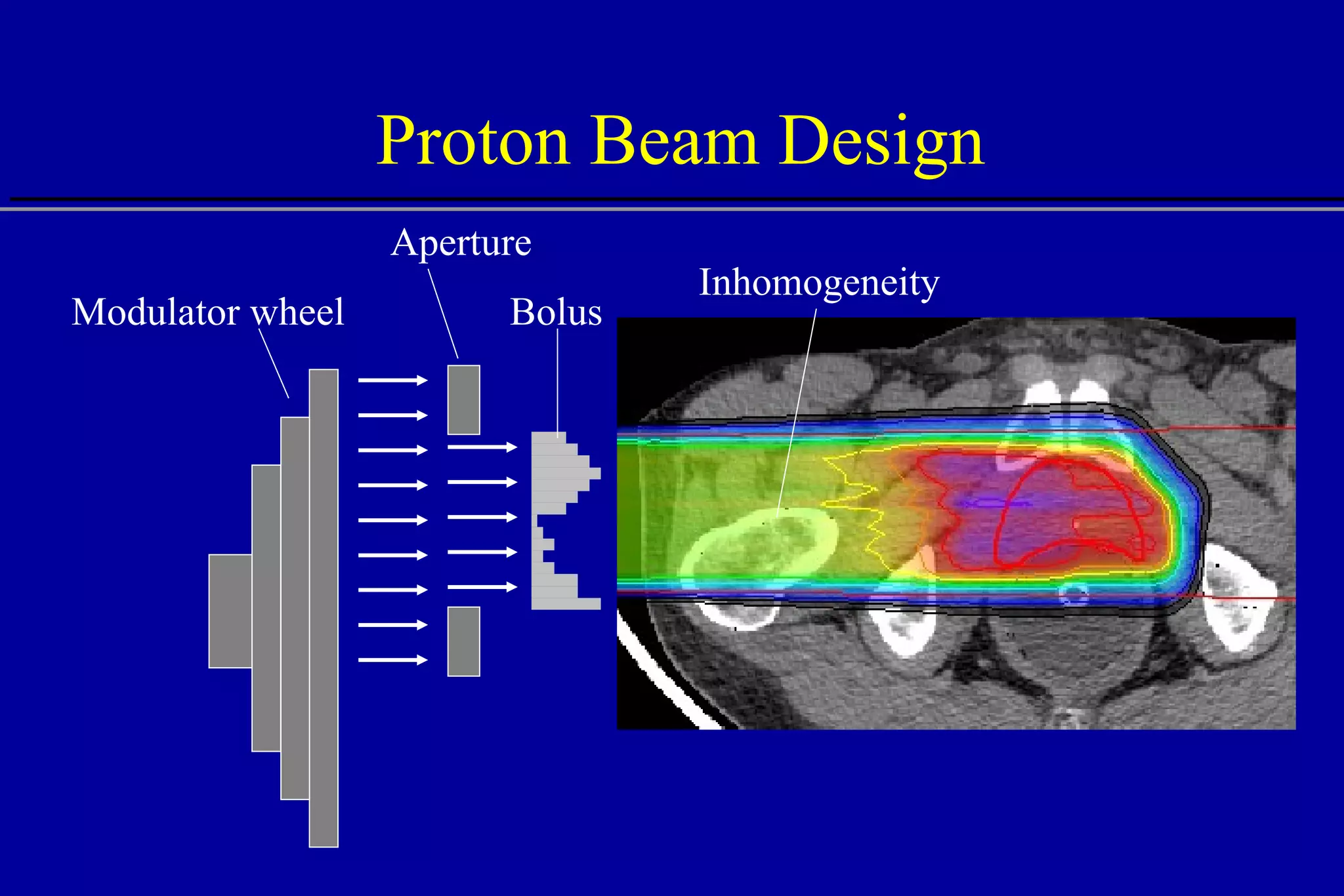
The document discusses the use of high-energy protons in cancer therapy. It provides a history of proton beam therapy beginning in 1946 when Robert Wilson first suggested its use. It describes the first proton treatment centers and worldwide growth of proton therapy facilities. Key advantages of protons over photons discussed include lower entrance dose and maximum dose at tumor depth. Challenges and uncertainties in proton therapy planning and delivery are also summarized.

1. The Use of High-Energy Protons in Cancer Therapy Reinhard W. Schulte Loma Linda University Medical Center

2. A Man - A Vision In 1946 Harvard physicist Robert Wilson (1914-2000) suggested * : Protons can be used clinically Accelerators are available Maximum radiation dose can be placed into the tumor Proton therapy provides sparing of normal tissues Modulator wheels can spread narrow Bragg peak *Wilson, R.R. (1946), “Radiological use of fast protons,” Radiology 47, 487.

3. History of Proton Beam Therapy 1946 R. Wilson suggests use of protons 1954 First treatment of pituitary tumors 1958 First use of protons as a neurosurgical tool 1967 First large-field proton treatments in Sweden 1974 Large-field fractionated proton treatments program begins at HCL, Cambridge, MA 1990 First hospital-based proton treatment center opens at Loma Linda University Medical Center

4. World Wide Proton Treatments * LLUMC (1990) 6174 HCL (1961) 6174 Uppsala (1957): 309 PSI (1984): 3935 Clatterbridge (1989): 1033 Nice (1991): 1590 Orsay (1991): 1894 Berlin (1998): 166 Chiba (1979) 133 Tsukuba (1983) 700 Kashiwa (1998) 75 NAC (1993) 398 Dubna (1967) 172 Moscow (1969) 3414 St. Petersburg (1969) 1029 *from: Particles, Newsletter (Ed J. Sisterson), No. 28. July 2001

5. LLUMC Proton Treatment Center Hospital-based facility Fixed beam line 40-250 MeV Synchrotron Gantry beam line

6. Main Interactions of Protons Electronic ( a ) ionization excitation Nuclear ( b-d ) Multiple Coulomb scattering ( b ), small  Elastic nuclear collision ( c ), large  Nonelastic nuclear interaction ( d ) e p p p’ p p p’ nucleus  n p’ p e nucleus (b) (c) (d) (a) 

7. Why Protons are advantageous Relatively low entrance dose (plateau) Maximum dose at depth (Bragg peak) Rapid distal dose fall-off Energy modulation (Spread-out Bragg peak) RBE close to unity Depth in Tissue Relative Dose 10 MeV X-rays Modulated Proton Beam Unmodulated Proton Beam

8. Uncertainties in Proton Therapy Patient setup Patient movements Organ motion Body contour Target definition Relative biological effectiveness (RBE) Device tolerances Beam energy Biology related: Patient related: Physics related: CT number conversion Dose calculation Machine related:

9. Treatment Planning Acquisition of imaging data (CT, MRI) Conversion of CT values into stopping power Delineation of regions of interest Selection of proton beam directions Design of each beam Optimization of the plan

10. Treatment Delivery Fabrication of apertures and boluses Beam calibration Alignment of patient using DRRs Computer-controlled dose delivery

11. Computed Tomography (CT) Faithful reconstruction of patient’s anatomy Stacked 2D maps of linear X-ray attenuation Electron density relative to water can be derived Calibration curve relates CT numbers to relative proton stopping power X-ray tube Detector array

12. Processing of Imaging Data CT Hounsfield values (H) Isodose distribution Calibration curve H = 1000  tissue /  water Relative proton stopping power (SP) SP = dE/dx tissue /dE/dx water Dose calculation H SP

13. Proton interaction  Photon interaction Bi- or tri- or multisegmental curves are in use No unique SP values for soft tissue Hounsfield range Tissue substitutes  real tissues Fat anomaly CT Calibration Curve

14. CT Calibration Curve Stoichiometric Method * Step 1: Parameterization of H Choose tissue substitutes Obtain best-fitting parameters A , B , C H = N e rel { A (Z PE ) 3.6 + B (Z coh ) 1.9 + C } Klein-Nishina cross section Rel. electron density Photo electric effect Coherent scattering *Schneider U. (1996), “The calibraion of CT Hounsfield units for radiotherapy treatment planning,” Phys. Med. Biol. 47, 487.

15. CT Calibration Curve Stoichiometric Method Step 2: Define Calibration Curve select different standard tissues with known composition (e.g., ICRP) calculate H using parametric equation for each tissue calculate SP using Bethe Bloch equation fit linear segments through data points Fat

16. CT Range Uncertainties Two types of uncertainties inaccurate model parameters beam hardening artifacts Expected range errors Soft tissue Bone Total H 2 O range abs. error H 2 O range abs. Error abs. error (cm) (mm) (cm) (mm) (mm) Brain 10.3 1.1 1.8 0.3 1.4 Pelvis 15.5 1.7 9 1.6 3.3 1 mm 4 mm

17. Proton Transmission Radiography - PTR First suggested by Wilson (1946) Images contain residual energy/range information of individual protons Resolution limited by multiple Coulomb scattering Spatial resolution of 1mm possible MWPC 2 MWPC 1 SC p Energy detector

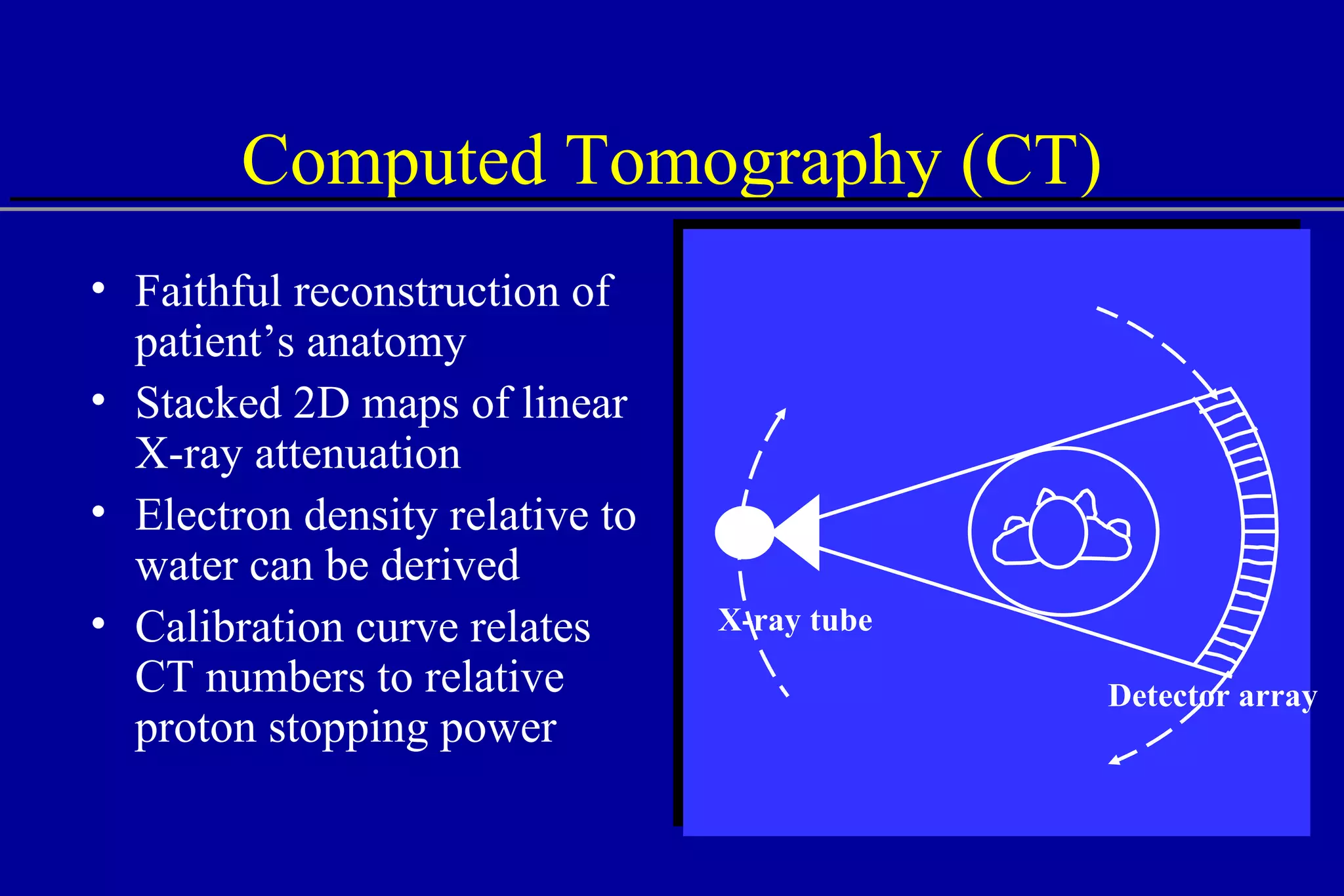
18. Comparison of CT Calibration Methods PTR used as a QA tool Comparison of measured and CT-predicted integrated stopping power Sheep head used as model Stoichiometric calibration (A) better than tissue substitute calibrations (B & C) SP calc - Sp meas [%] No of PTR pixels [%]

19. Proton Beam Computed Tomography Proton CT for diagnosis first studied during the 1970s dose advantage over x rays not further developed after the advent of X-ray CT Proton CT for treatment planning and delivery renewed interest during the 1990s (2 Ph.D. theses) preliminary results are promising further R&D needed

20. Proton Beam Computed Tomography Conceptual design single particle resolution 3D track reconstruction Si microstrip technology cone beam geometry rejection of scattered protons & neutrons DAQ Trigger logic Si MS 2 ED Si MS 1 Si MS 3 SC x p cone beam

21. Proton Beam Design Modulator wheel Aperture Bolus Inhomogeneity

22. Proton Beam Shaping Devices Cerrobend aperture Wax bolus Modulating wheels

23. Ray-Tracing Dose Algorithm One-dimensional dose calculation Water-equivalent depth (WED) along single ray SP Look-up table Reasonably accurate for simple hetero-geneities Simple and fast || WED S P

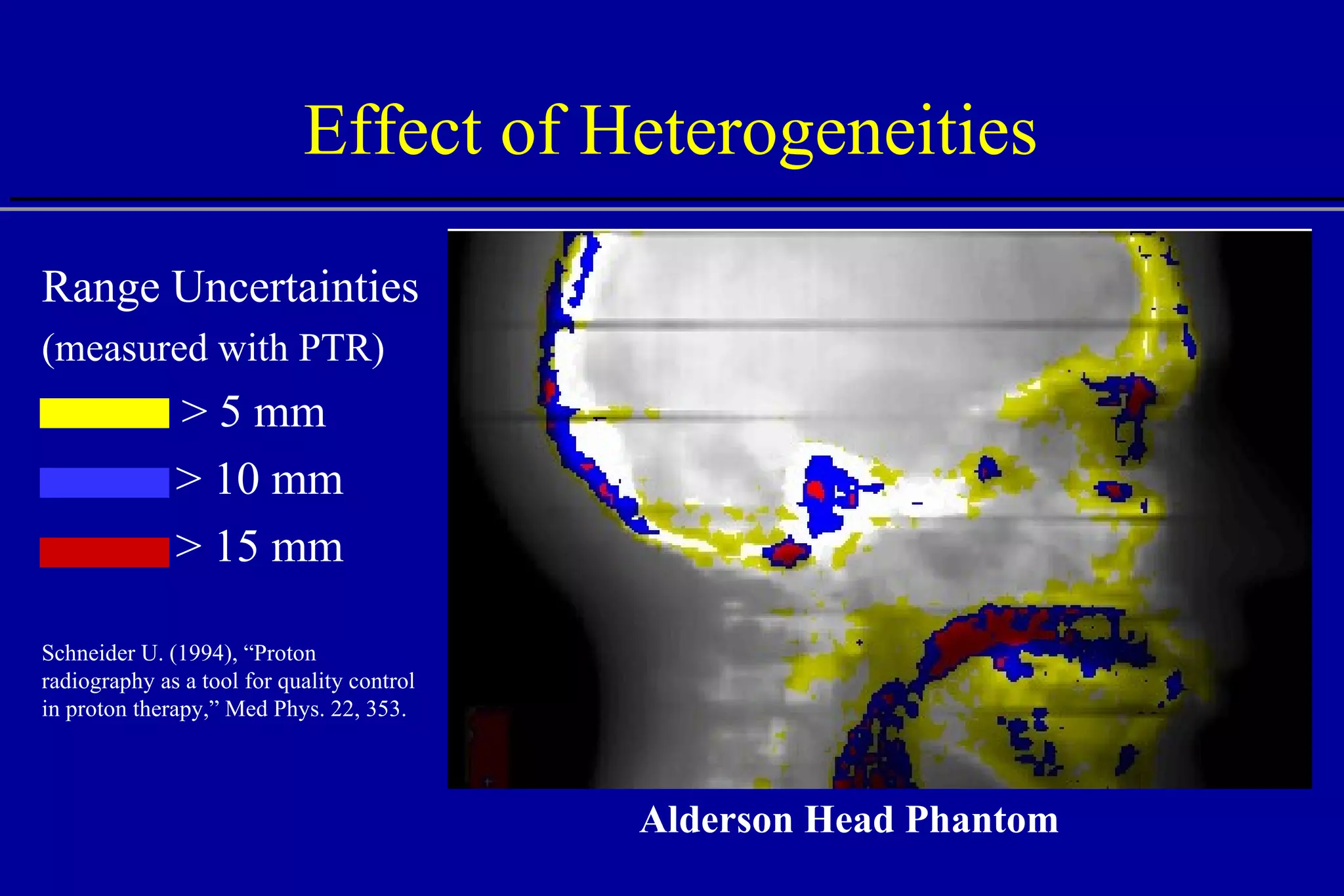
24. Effect of Heterogeneities W = 10 mm W = 4 mm W = 2 mm W = 1 mm W = 1 mm No heterogeneity Bone Water Protons W Central axis Depth [cm] 15 5 10 Central axis dose

25. Effect of Heterogeneities Range Uncertainties (measured with PTR) > 5 mm > 10 mm > 15 mm Schneider U. (1994), “Proton radiography as a tool for quality control in proton therapy,” Med Phys. 22, 353. Alderson Head Phantom

26. Pencil Beam Dose Algorithm Cylindrical coordinates Measured or calculated pencil kernel Water-equivalent depth Accounts for multiple Coloumb scattering more time consuming WED S P

27. Monte Carlo Dose Algorithm Considered as “gold standard” Accounts for all relevant physical interactions Follows secondary particles Requires accurate cross section data bases Includes source geometry Very time consuming

28. Comparison of Dose Algorithms Protons Petti P. (1991), “Differential-pencil-beam dose calculations for charged particles,” Med Phys. 19, 137. Bone Water Monte Carlo Ray-tracing Pencil beam

29. Combination of Proton Beams “ Patch-field” design Targets wrapping around critical structures Each beam treats part of the target Accurate knowledge of lateral and distal penumbra is critical Urie M. M. et al (1986), “Proton beam penumbra: effects of separation between patient and beam modifying devices,” Med Phys. 13, 734.

30. Combination of Proton Beams Excellent sparing of critical structures No perfect match between fields Dose non-uniformity at field junction “ hot” and “cold” regions are possible Clinical judgment required Lateral field Patch field 2 Patch field 1 Critical structure

31. Lateral Penumbra Penumbra factors: Upstream devices scattering foils range shifter modulator wheel bolus Air gap Patient scatter Air gap 100 80 0 60 40 20 25 0 20 15 10 5 Distance [mm] % Dose B A A - no air gap B - 40 cm air gap 80%-20% 80%-20%

32. Lateral Penumbra Thickness of bolus  , width of air gap   lateral penumbra  Dose algorithms can be inaccurate in predicting penumbra Russel K. P. et al (2000), “Implementation of pencil kernel and depth penetration algorithms for treatment planning of proton beams,” Phys Med Biol 45, 9. 10 8 0 6 4 2 16 0 12 8 4 no bolus Measurement 5 cm bolus 20-80% penumbra Air gap [cm] Pencil beam Ray tracing

33. Nuclear Data for Treatment Planning (TP) Experiment Theory Evaluation Radiation Transport Codes for TP ‡ Validation Quality Assurance Recommended Data † † e.g., ICRU Report 63 ‡ e.g., Peregrine Integral tests, benchmarks

34. Nuclear Data for Proton Therapy Application Quantities needed Loss of primary protons Total nonelastic cross sections Dose calculation, radiation Diff. and doublediff. cross sections transport for neutron, charged particles, and  emission Estimation of RBE average energies for light ejectiles product recoil spectra PET beam localization Activation cross sections

35. Selection of Elements Element Mainly present in ’ H, C, O Tissue, bolus N, P Tissue, bone Ca Bone, shielding materials Si Detectors, shielding materials Al, Fe, Cu, W, Pb Scatterers, apertures, shielding materials

36. Nuclear Data for Proton Therapy Internet sites regarding nuclear data: International Atomic Energy Agency (Vienna) Online telnet access of Nuclear Data Information System Brookhaven National Laboratory Online telnet access of National Nuclear Data Center Los Alamos National Laboratory T2 Nuclear Information System. OECD Nuclear Energy Agency NUKE - Nuclear Information World Wide Web

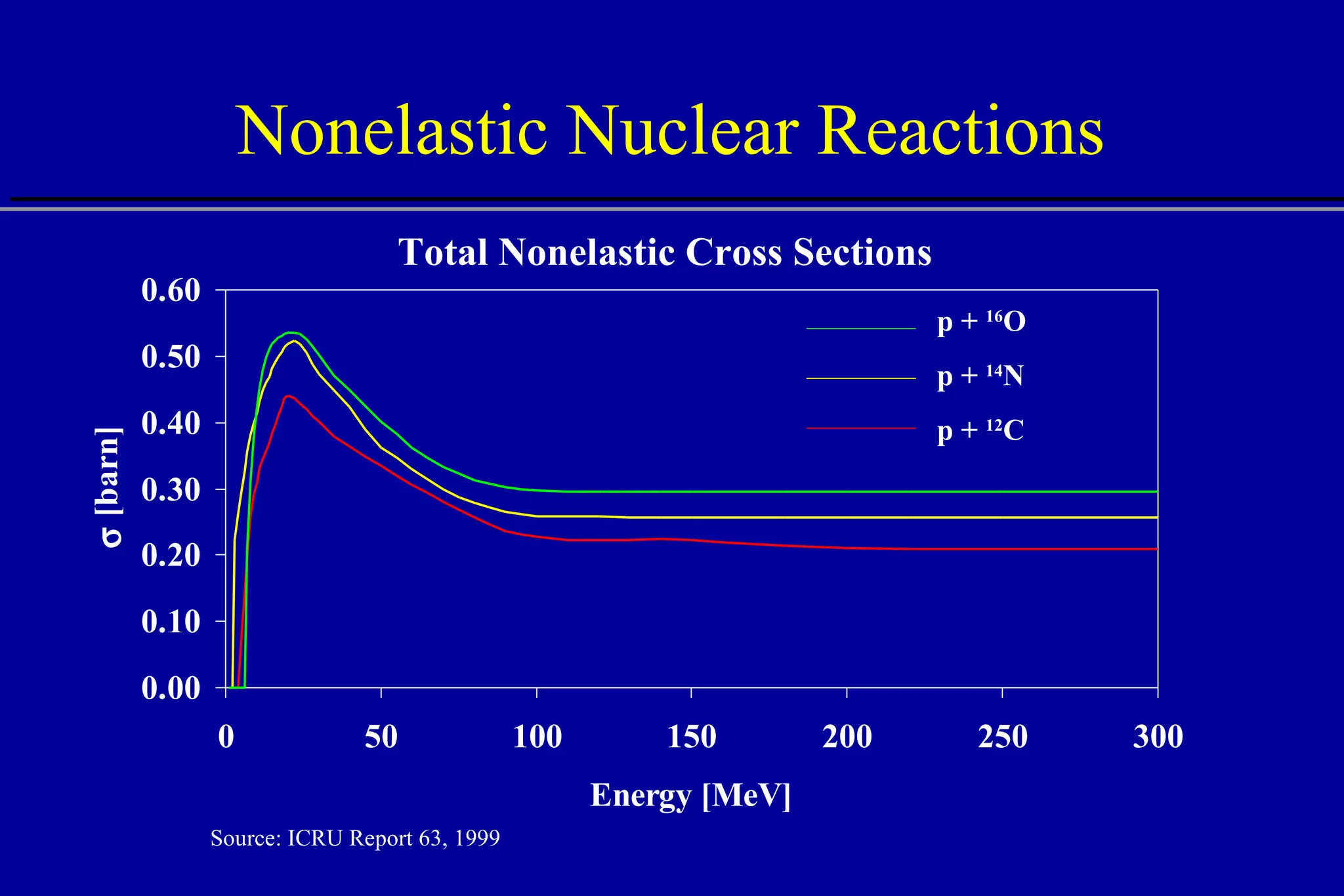
37. Nonelastic Nuclear Reactions Remove primary protons Contribute to absorbed dose: 100 MeV, ~5% 150 MeV, ~10% 250 MeV, ~20% Generate secondary particles neutral (n,  ) charged (p, d, t, 3 He,  , recoils) 40 0 10 15 20 25 30 35 5 250 MeV Depth [cm] Energy Deposition (dE/dx) All interactions Electronic interactions Nuclear interactions

38. Nonelastic Nuclear Reactions Source: ICRU Report 63, 1999 Total Nonelastic Cross Sections p + 16 O p + 14 N p + 12 C

39. Proton Beam Activation Products Activation Product Application / Significance Short-lived  + emitters in-vivo dosimetry (e.g., 11 C, 13 N, 18 F) beam localization 7 Be none Medium mass products none (e.g., 22 Na, 42 K, 48 V, 51 Cr) Long-lived products in radiation protection collimators, shielding

40. Positron Emission Tomography (PET) of Proton Beams Reaction Half-life Threshold Energy (MeV) e 16 O(p,pn) 15 O 2.0 min 16.6 16 O(p,2p2n) 13 N 10.0 min 5.5 16 O(p,3p3n) 13 C 20.3 min 14.3 14 N(p,pn) 13 N 10.0 min 11.3 14 N(p,2p2n) 11 C 20.3 min 3.1 12 C(p,pn) 17 N 20.3 min 20.3

41. PET Dosimetry and Localization Experiment vs. simulation activity plateau (experiment) maximum activity (simulation) cross sections may be inaccurate activity fall-off 4-5 mm before Bragg peak Del Guerra A., et al. (1997) “PET Dosimetry in proton radiotherapy: a Monte Carlo Study,” Appl. Radiat. Isot. 10-12, 1617. 2 4 6 8 10 0 Depth [cm] Activity dE/dx PET experiment calculated activity calculated energy deposition 110 MeV p on Lucite, 24 min after irradiation

42. PET Localization for Functional Proton Radiosurgery Treatment of Parkinson’s disease Multiple narrow p beams of high energy (250 MeV) Focused shoot-through technique Very high local dose (> 100 Gy) PET verification possible after test dose

43. Relative Biological Effectiveness (RBE) Clinical RBE: 1 Gy proton dose  1.1 Gy Cobalt  dose (RBE = 1.1) RBE vs. depth is not constant RBE also depends on dose biological system (cell type) clinical endpoint (early response, late effect)

44. Linear Energy Transfer (LET) vs. Depth 100 MeV 250 MeV 40 MeV Depth

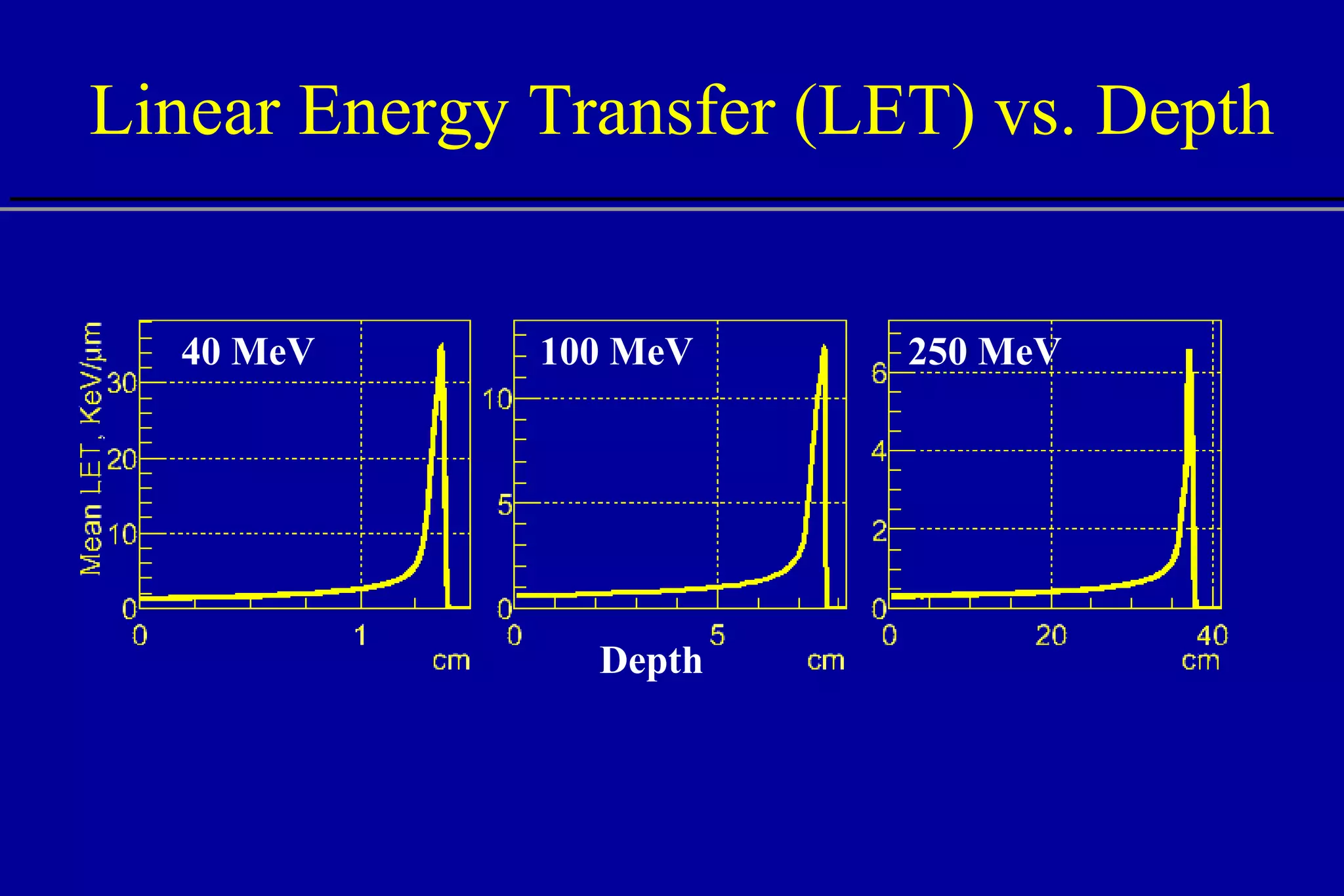
45. RBE vs. LET Source: S.M. Seltzer, NISTIIR 5221 10 0 10 2 10 3 10 4 10 1 0.0 2.0 3.0 4.0 5.0 6.0 LET [keV/  m] RBE 1.0 high low

46. RBE of a Modulated Proton Beam Source: S.M. Seltzer, NISTIIR 5221 1.7 4 6 8 12 14 16 18 20 0 10 2 0.8 0.6 0.2 0.4 0.9 0.0 1.1 1.2 1.3 1.4 1.5 1.6 1.0 Modulated beam 160 MeV Depth [cm] RBE low high Relative dose 1.0 Clinical RBE

47. Open RBE Issues Single RBE value of 1.1 may not be sufficient Biologically effective dose vs. physical dose Effect of proton nuclear interactions on RBE Energy deposition at the nanometer level - clustering of DNA damage

48. Summary Areas where (high-energy) physics may contribute to proton radiation therapy: Development of proton computed tomography Nuclear data evaluation and benchmarking Radiation transport codes for treatment planning In vivo localization and dosimetry of proton beams Influence of nuclear events on RBE