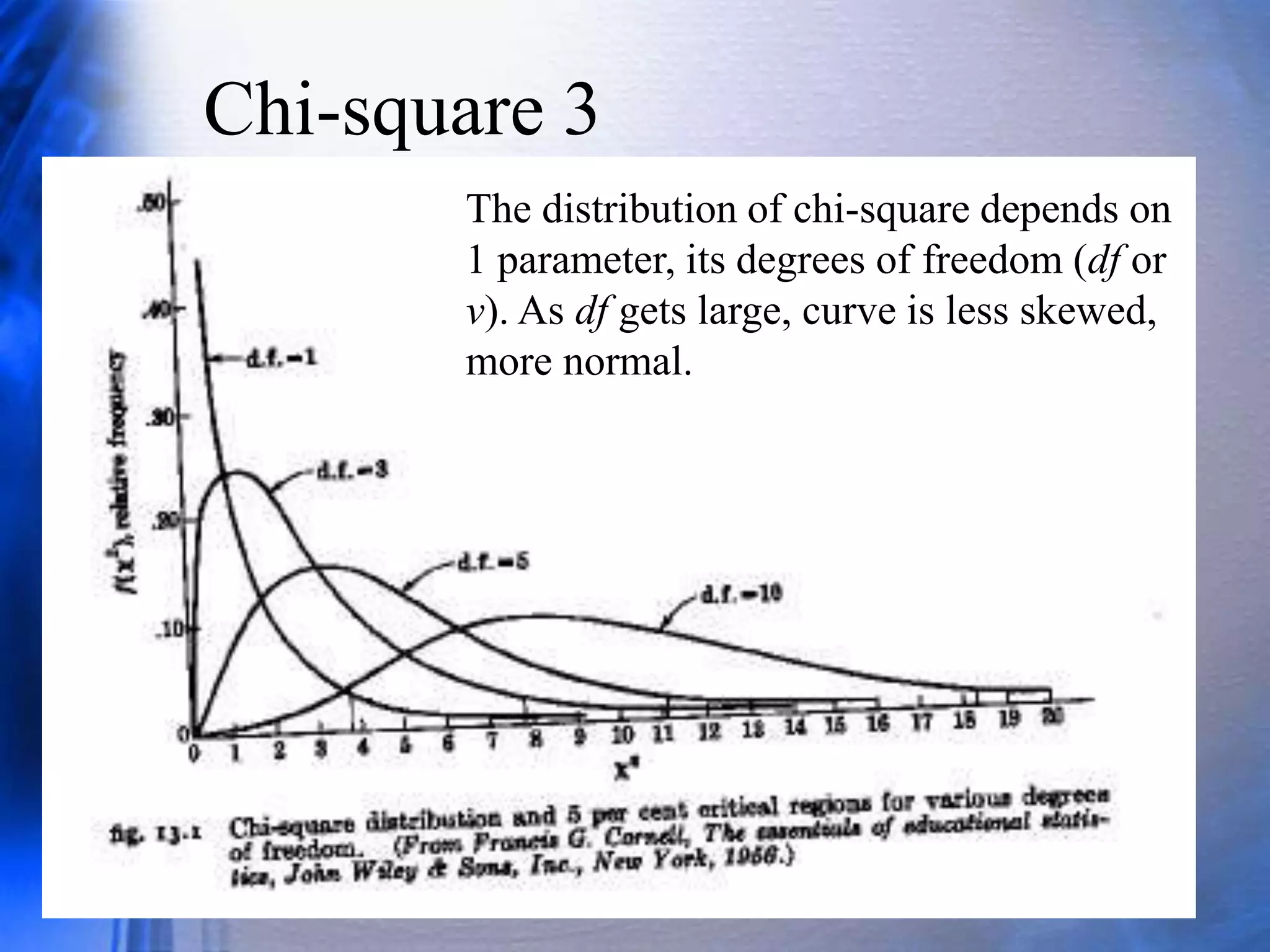
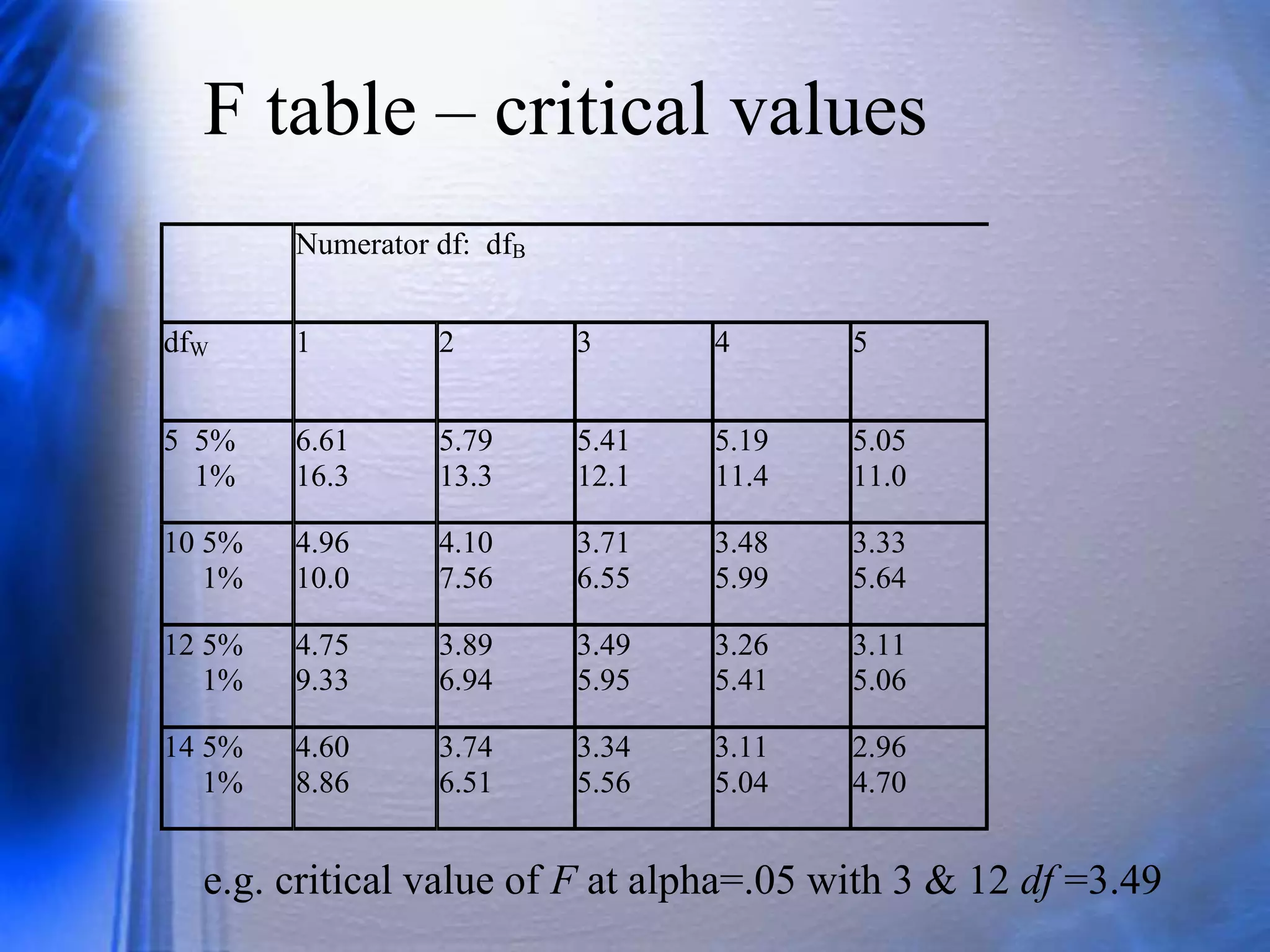
The chi-square distribution is related to the normal distribution, as it is the distribution of the sum of squared normal random variables. The F distribution is the ratio of two chi-square random variables, each divided by its degrees of freedom. Both the chi-square and F distributions are used to test hypotheses about variances and compare variance estimates. To test if two samples have equal variances, the F test compares the ratio of the two sample variance estimates to the critical values of the F distribution with the degrees of freedom of each sample.

1. Chi-square and F Distributions
Children of the Normal

2. Questions
• What is the chi-square distribution?
How is it related to the Normal?
• How is the chi-square distribution
related to the sampling distribution of
the variance?
• Test a population value of the variance;
put confidence intervals around a
population value.

3. Questions
• How is the F distribution related the
Normal? To Chi-square?

4. Distributions
• There are many theoretical
distributions, both continuous and
discrete. Howell calls these test
statistics
• We use 4 test statistics a lot: z (unit
normal), t, chi-square ( ), and F.
• Z and t are closely related to the
sampling distribution of means; chi-
square and F are closely related to the
sampling distribution of variances.
2


5. Chi-square Distribution (1)

)
(
;
)
( 



X
z
SD
X
X
z
2
2
2 )
(




X
z
z score
z score squared
2
)
1
(
2


z Make it Greek
What would its sampling distribution look like?
Minimum value is zero.
Maximum value is infinite.
Most values are between zero and 1;
most around zero.

6. Chi-square (2)
What if we took 2 values of z2 at random and added them?
2
2
2
2
2
2
2
1
2
1
)
(
;
)
(



 



X
z
X
z 2
2
2
1
2
2
2
2
2
1
2
)
2
(
)
(
)
(
z
z
X
X











Chi-square is the distribution of a sum of squares.
Each squared deviation is taken from the unit normal:
N(0,1). The shape of the chi-square distribution
depends on the number of squared deviates that are
added together.
Same minimum and maximum as before, but now average
should be a bit bigger.

7. Chi-square 3
The distribution of chi-square depends on
1 parameter, its degrees of freedom (df or
v). As df gets large, curve is less skewed,
more normal.

8. Chi-square (4)
• The expected value of chi-square is df.
– The mean of the chi-square distribution is its
degrees of freedom.
• The expected variance of the distribution is
2df.
– If the variance is 2df, the standard deviation must
be sqrt(2df).
• There are tables of chi-square so you can find
5 or 1 percent of the distribution.
• Chi-square is additive. 2
)
(
2
)
(
2
)
( 2
1
2
1 v
v
v
v 

 



9. Distribution of Sample
Variance
1
)
( 2
2




N
y
y
s
Sample estimate of population variance
(unbiased).
2
2
2
)
1
(
)
1
(


s
N
N



Multiply variance estimate by N-1 to
get sum of squares. Divide by
population variance to stadnardize.
Result is a random variable distributed
as chi-square with (N-1) df.
We can use info about the sampling distribution of the
variance estimate to find confidence intervals and
conduct statistical tests.

10. Testing Exact Hypotheses
about a Variance
2
0
2
0 : 
 
H Test the null that the population
variance has some specific value. Pick
alpha and rejection region. Then:
2
0
2
2
)
1
(
)
1
(


s
N
N



Plug hypothesized population
variance and sample variance into
equation along with sample size we
used to estimate variance. Compare
to chi-square distribution.

11. Example of Exact Test
Test about variance of height of people in inches. Grab 30
people at random and measure height.
55
.
4
;
30
.
25
.
6
:
;
25
.
6
:
2
2
1
2
0




s
N
H
H 
 Note: 1 tailed test on
small side. Set alpha=.01.
11
.
21
25
.
6
)
55
.
4
)(
29
(
2
29 


Mean is 29, so it’s on the small
side. But for Q=.99, the value
of chi-square is 14.257.
Cannot reject null.
55
.
4
;
30
.
25
.
6
:
;
25
.
6
:
2
2
1
2
0




s
N
H
H 

Now chi-square with v=29 and Q=.995 is 13.121 and
also with Q=.005 the result is 52.336. N. S. either way.
Note: 2 tailed with alpha=.01.

12. Confidence Intervals for the
Variance
We use to estimate . It can be shown that:
2
s
2

95
.
)
1
(
)
1
(
2
)
975
;.
1
(
2
2
2
)
025
;.
1
(
2








 




 N
N
s
N
s
N
p



Suppose N=15 and is 10. Then df=14 and for Q=.025
the value is 26.12. For Q=.975 the value is 5.63.
95
.
63
.
5
)
10
)(
14
(
12
.
26
)
10
)(
14
( 2








 
p
  95
.
87
.
24
36
.
5 2


 
p
2
s

13. Normality Assumption
• We assume normal distributions to figure
sampling distributions and thus p levels.
• Violations of normality have minor
implications for testing means, especially as
N gets large.
• Violations of normality are more serious for
testing variances. Look at your data before
conducting this test. Can test for normality.

14. Review
• You have sample 25 children from an
elementary school 5th grade class and
measured the height of each. You
wonder whether these children are more
variable in height than typical children.
Their variance in height is 4. Compute
a confidence interval for this variance.
If the variance of height in children in
5th grade nationally is 2, do you
consider this sample ordinary?

15. The F Distribution (1)
• The F distribution is the ratio of two
variance estimates:
• Also the ratio of two chi-squares, each
divided by its degrees of freedom:
2
2
2
1
2
2
2
1
.
.


est
est
s
s
F 

2
2
(
1
2
)
(
/
)
/
2
1
v
v
F
v
v



In our applications, v2 will be larger
than v1 and v2 will be larger than 2.
In such a case, the mean of the F
distribution (expected value) is
v2 /(v2 -2).

16. F Distribution (2)
• F depends on two parameters: v1 and
v2 (df1 and df2). The shape of F
changes with these. Range is 0 to
infinity. Shaped a bit like chi-square.
• F tables show critical values for df in
the numerator and df in the
denominator.
• F tables are 1-tailed; can figure 2-tailed
if you need to (but you usually don’t).

17. F table – critical values
Numerator df: dfB
dfW 1 2 3 4 5
5 5%
1%
6.61
16.3
5.79
13.3
5.41
12.1
5.19
11.4
5.05
11.0
10 5%
1%
4.96
10.0
4.10
7.56
3.71
6.55
3.48
5.99
3.33
5.64
12 5%
1%
4.75
9.33
3.89
6.94
3.49
5.95
3.26
5.41
3.11
5.06
14 5%
1%
4.60
8.86
3.74
6.51
3.34
5.56
3.11
5.04
2.96
4.70
e.g. critical value of F at alpha=.05 with 3 & 12 df =3.49

18. Testing Hypotheses about 2
Variances
• Suppose
– Note 1-tailed.
• We find
• Then df1=df2 = 15, and
2
2
2
1
1
2
2
2
1
0 :
;
: 


 
 H
H
7
.
1
;
16
;
8
.
5
;
16 2
2
2
2
1
1 


 s
N
s
N
41
.
3
7
.
1
8
.
5
2
2
2
1



s
s
F Going to the F table with 15
and 15 df, we find that for alpha
= .05 (1-tailed), the critical
value is 2.40. Therefore the
result is significant.

19. A Look Ahead
• The F distribution is used in many
statistical tests
– Test for equality of variances.
– Tests for differences in means in ANOVA.
– Tests for regression models (slopes
relating one continuous variable to another
like SAT and GPA).

20. Relations among Distributions
– the Children of the Normal
• Chi-square is drawn from the normal.
N(0,1) deviates squared and summed.
• F is the ratio of two chi-squares, each
divided by its df. A chi-square divided
by its df is a variance estimate, that is,
a sum of squares divided by degrees of
freedom.
• F = t2. If you square t, you get an F
with 1 df in the numerator.
)
,
1
(
2
)
( v
v F
t 

21. Review
• How is F related to the Normal? To
chi-square?
• Suppose we have 2 samples and we
want to know whether they were drawn
from populations where the variances
are equal. Sample1: N=50, s2=25;
Sample 2: N=60, s2=30. How can we
test? What is the best conclusion for
these data?