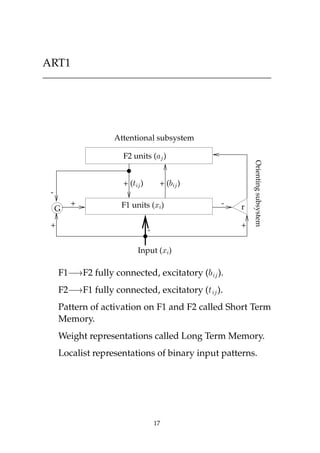
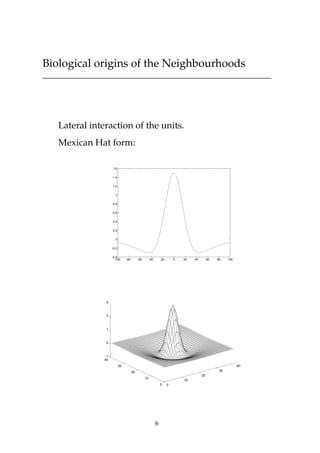
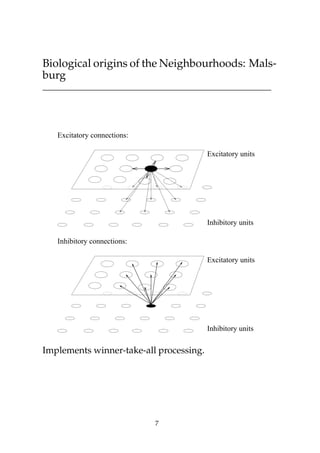
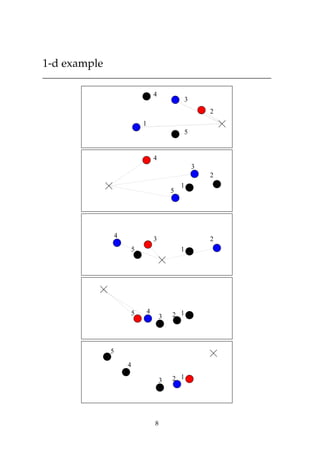
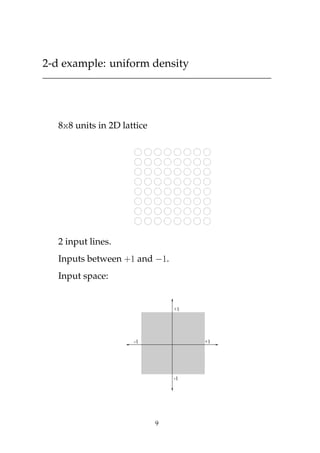
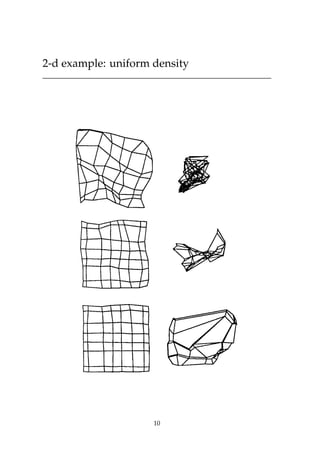
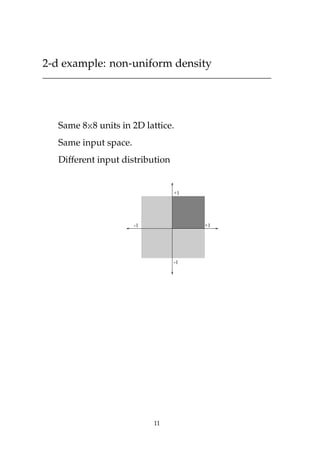
This document discusses self-organizing neural networks, including Kohonen networks and Adaptive Resonance Theory (ART). It provides details on Kohonen networks such as their basic structure, learning algorithm using neighborhoods, and biological origins. ART is introduced as a way to address the stability-plasticity dilemma in neural networks. The key aspects of ART1 are summarized, including its orienting and attentional subsystems, short and long term memory representations, and learning algorithm using a vigilance test. Examples of a Kohonen network and ART1 network are also included to illustrate their operation.

1. Self Organising Neural Networks
Kohonen Networks.
A Problem with Neural Networks.
ART.
Beal, R. and Jackson, T. (1990). Neural Computing: An Introduction.
Chapters 5 & 7. Adam Hilger, NY.
Hertz, J., Krogh, A. and Palmer, R. (1991). Introduction to the Theory
of Neural Computation. Chapter 9. Addison–Wesley. NY.
Grossberg, S. (1987). Competitive Learning: from interactive acti-
vation to adaptive resonance. Cognitive Science, 11: 23–63.
1

2. Kohonen Self Organising Networks
Kohonen, T. (1982). Self–organized formation of topologically cor-
rect feature maps., Biological Cybernetics, 43: 59–69.
An abstraction from earlier models (e.g. Malsburg,
1973).
The formation of feature maps (introducing a geo-
metric layout).
Popular and useful.
Can be traced to biologically inspired origins.
Why have topographic mappings?
– Minimal wiring
– Help subsequent processing layers.
Example: Xenopus retinotectal mapping (Price & Will-
shaw 2000, p121).
2

3. Basic Kohonen Network
Geometric arrangement of units.
Units respond to “part” of the environment.
Neighbouring units should respond to similar parts
of the environment.
Winning unit selected by:
Ü Û min Ü Û
where Û is the weight vector of winning unit, and
Ü is the input pattern.
and Neighbourhoods...
3

4. Neighbourhoods in the Kohonen Network
Example in 2D.
Neighbourhood of winning unit called Æ .
4

5. Learning in the Kohonen Network
All units in Æ are updated.
dÛ
dØ
«´Øµ Ü ´Øµ Û ´Øµ for ¾ Æ
¼ otherwise
where
dÛ
dØ
= change in weight over time.
«´Øµ = time dependent learning parameter.
Ü ´Øµ = input component at time Ø.
Û ´Øµ = weight from input to unit at time Ø.
¯ Geometrical effect: move weight vector closer to in-
put vector.
¯ « is strongest for winner and can decrease with dis-
tance. Also decreases over time for stability.
5

6. Biological origins of the Neighbourhoods
Lateral interaction of the units.
Mexican Hat form:
-100 -80 -60 -40 -20 0 20 40 60 80 100
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
0
10
20
30
40
0
10
20
30
40
-1
0
1
2
3
6

7. Biological origins of the Neighbourhoods: Mals-
burg
Inhibitory connections:
Excitatory units
Inhibitory units
Excitatory units
Inhibitory units
Excitatory connections:
Implements winner-take-all processing.
7

8. 1-d example
1
4
3
2
5
5
4
2
1
3
5
2
1
3
4
4 15 3 2
4
1
3 2
5
8

9. 2-d example: uniform density
8x8 units in 2D lattice
2 input lines.
Inputs between ·½ and ½.
Input space:
+1
+1
-1
-1
9

10. 2-d example: uniform density
10

11. 2-d example: non-uniform density
Same 8x8 units in 2D lattice.
Same input space.
Different input distribution
+1
+1
-1
-1
11

12. 2-d example: non-uniform density
12

13. 2-d µ1-d example: dimension reduction
2-d input uniform density; 1-d output arrangement.
“Space-filling” (Peano) curves; can solve Travelling
Salesman Problem.
init wts epoch 10
epoch 500 epoch 700
13

14. Example Application of Kohonen’s Network
The Phonetic Typewriter
MP Filter A/D
FFT
Rules
Kohonen
Network
Problem: Classification of phonemes in real time.
Pre and post processing.
Network trained on time sliced speech wave forms.
Rules needed to handle co-articulation effects.
14

15. A Problem with Neural Networks
Consider 3 network examples:
Kohonen Network.
Associative Network.
Feed Forward Back-propagation.
Under the situation:
Network learns environment (or I/O relations).
Network is stable in the environment.
Network is placed in a new environment.
What happens:
Kohonen Network won’t learn.
Associative Network OK.
Feed Forward Back-propagation Forgets.
called The Stability/Plasticity Dilemma.
15

16. Adaptive Resonance Theory
Grossberg, S. (1976a). Adaptive pattern classification and univer-
sal recoding I: Feedback, expectation, olfaction, illusions. Biological
Cybernetics, 23: 187–202.
a “neural network that self–organize[s] stable pat-
tern recognition codes in real time, in response to
arbitrary sequences of input patterns”.
ART1 (1976). Localist representation, binary patterns.
ART2 (1987). Localist representation, analog patterns.
ART3 (1990). Distributed representation, analog pat-
terns.
Desirable properties:
plastic + stable
biological mechanisms
analytical math foundation
16

17. ART1
Orientingsubsystem
+
+
-
+
+ ( )
G
+ (Ø )
r-
+
Attentional subsystem
Input (Ü )
F2 units ( )
F1 units (Ü )
F1 F2 fully connected, excitatory ( ).
F2 F1 fully connected, excitatory (Ø ).
Pattern of activation on F1 and F2 called Short Term
Memory.
Weight representations called Long Term Memory.
Localist representations of binary input patterns.
17

18. Summary of ART 1
(Lippmann, 1987). N = number of F1 units.
Step 1: Initialization
Ø ½ ½
½·Æ
Set vigilance parameter ¼ ½
Step 2: apply new input (binary Ü )
Step 3: compute F2 activation
Æ
½
Ü
Step 4: find best matching node , where .
Step 5: vigilance test
Æ
½
Ü Ì ¡
Æ
½
Ø Ü
Is
Ì ¡
If no, go to step 6. If yes go to step 7.
Step 6: mismatch/reset: set ¼ and go to step 4.
Step 7: resonance — adapt best match
Ø Ø Ü
Ø
·
ÈÆ
½ Ø Ü
Step 8: Re-enable all F2 units and go to step 2
18

19. ART1: Example
INPUT
UNIT 1 UNIT 2
resonance
resonance
1st choice
reset
resonance
1st choice
reset
2nd choice
reset
resonance
1st choice
reset
2nd choice
resetreset
3rd choice resonance
UNIT 3 UNIT 4
1st choice
resonance
1st choice
reset
2nd choice
resonance
1st choice
reset
2nd choice
reset
3rd choice
resetreset
4th choice resonance
UNIT 5
F2 UNITS REPRESENT:
19

20. Summary
Simple?
Interesting biological parallels.
Diverse applications.
Extensions.
20