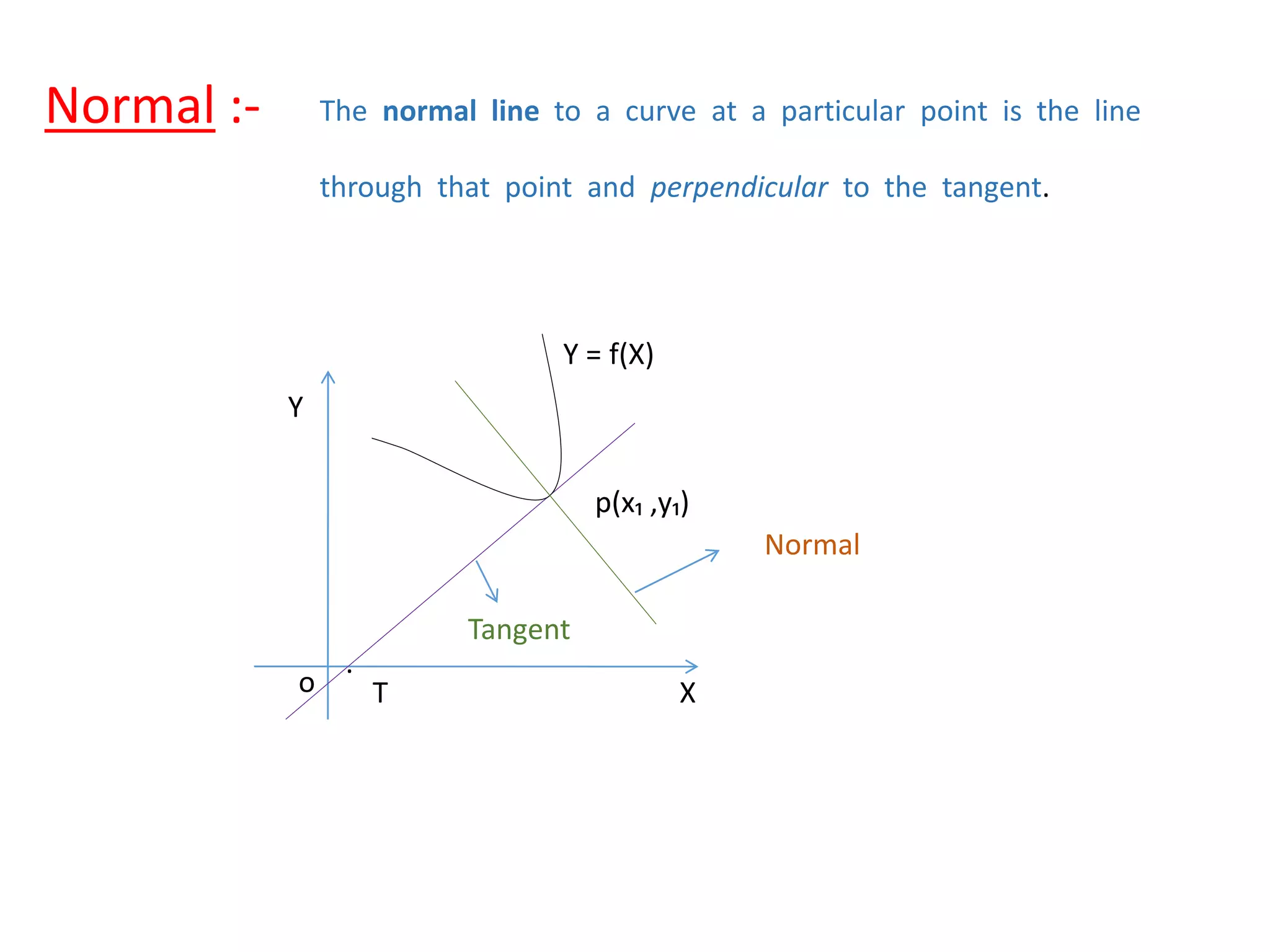
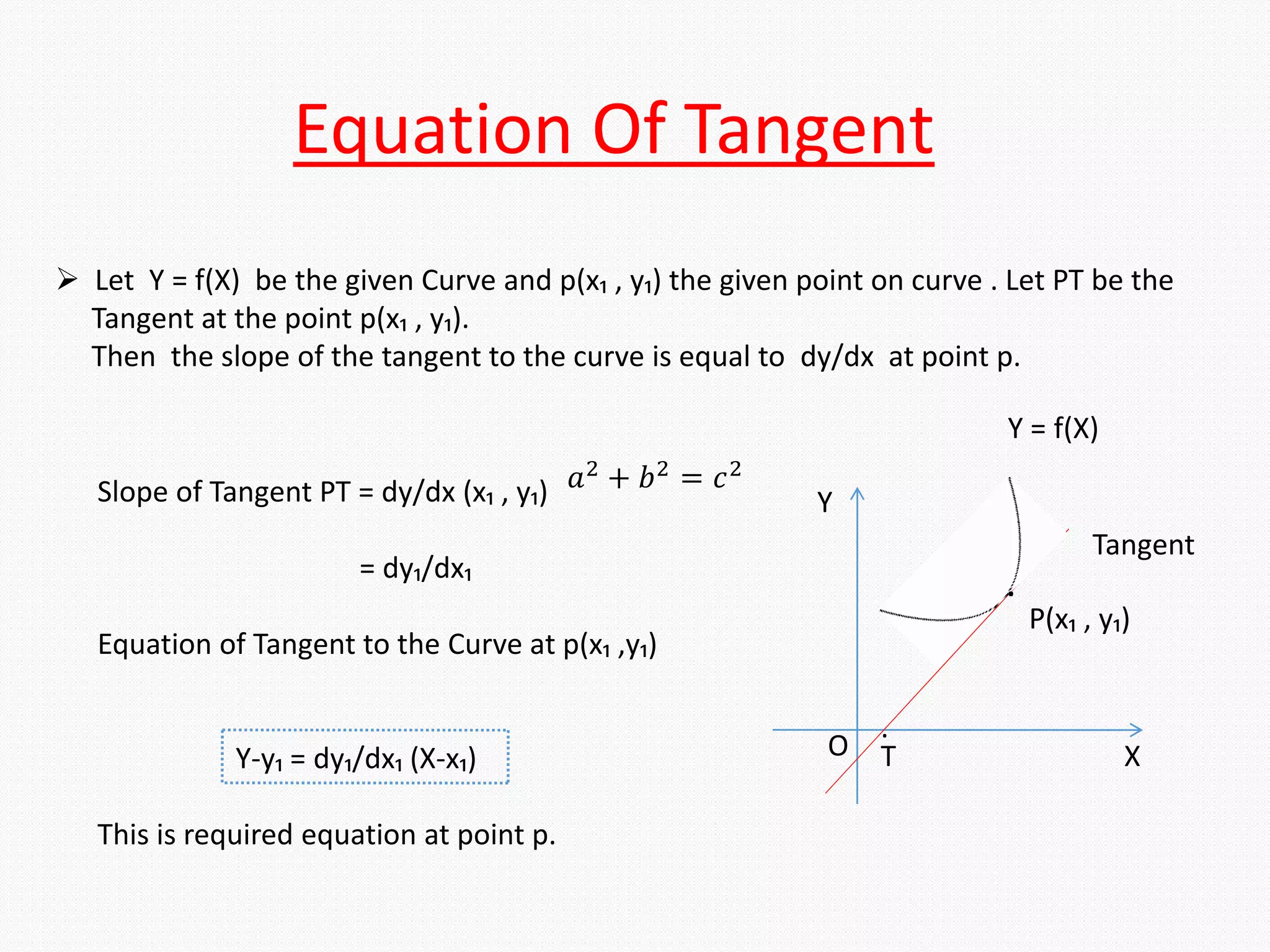
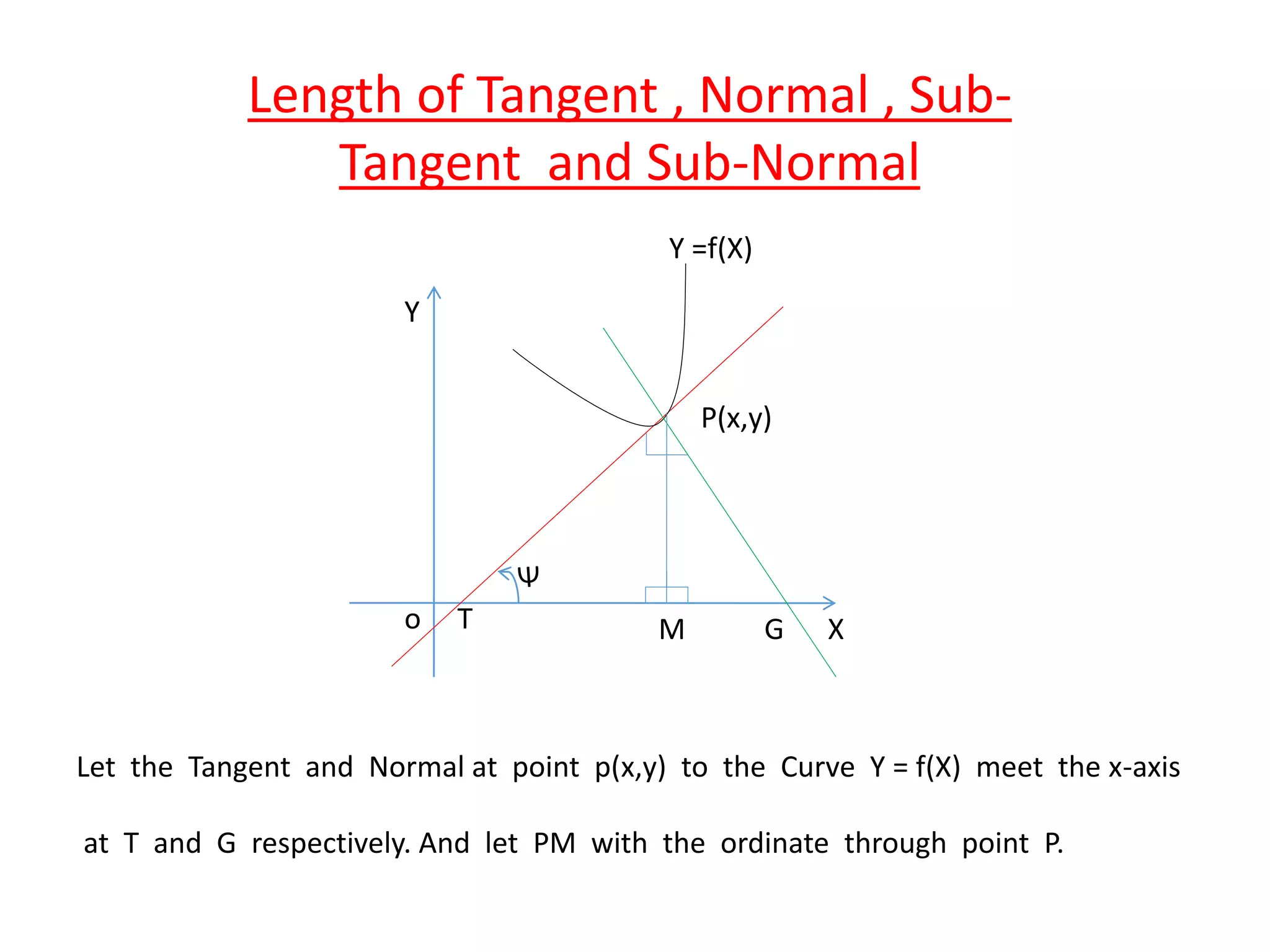
This document defines tangent and normal lines to a curve and provides equations for tangent and normal lines. It also defines the length of the tangent, normal, sub-tangent, and sub-normal. Specifically, it defines a tangent line as one that touches a curve at only one point and a normal line as perpendicular to the tangent line at a given point. It provides the equations for finding the slope and equation of the tangent and normal lines at any given point. It also gives formulas for calculating the length of the tangent, normal, sub-tangent, and sub-normal in terms of the curve's equation and derivatives at a given point.

1. Tangent And Normal
Presented By:- Ramesh Singh Makar Presented To:- Mr. Sunil Bhardwaj

2. 1. Definition
• Tangent
• Normal
2. Equation
• Tangent
• Normal
3. Length Of Tangent, Sub-Tangent, Length Of Normal, Sub-Normal
CONTENTS

3. Tangent :-A tangent is a line that touches a curve. A tangent meets or touches a
circle only at one point, whereas the tangent line can meet a curve at
more than one point.
(1) (2)
 On the other hand, a line may meet the curve once, but still not be a tangent

4. The normal line to a curve at a particular point is the line
through that point and perpendicular to the tangent.
Normal :-
X
Y
p(x₁ ,y₁)
.
T
Normal
Tangent
Y = f(X)
o

5. Equation Of Tangent
 Let Y = f(X) be the given Curve and p(x₁ , y₁) the given point on curve . Let PT be the
Tangent at the point p(x₁ , y₁).
Then the slope of the tangent to the curve is equal to dy/dx at point p.
Slope of Tangent PT = dy/dx (x₁ , y₁)
= dy₁/dx₁
Equation of Tangent to the Curve at p(x₁ ,y₁)
Y-y₁ = dy₁/dx₁ (X-x₁)
This is required equation at point p.
.
P(x₁ , y₁)
Y = f(X)
Tangent
Y
X
·
T
O
𝑎2
+ 𝑏2
= 𝑐2

6. Equation Of Normal
 We Know that,
Normal is perpendicular to the Tangent at point p(x₁ , y₁) .
So…….
(slope of Tangent at p)(slope of Normal at p) = -1
m₁m₂ = -1 m₂ = -dx₁/dy₁
Required Equation of Tangent at point p(x₁ , y₁) Is……
Y-y₁ = (- dx₁/dy₁)(X-x₁)
Y = f(x)
Tangent
Normal
p(x₁ ,y₁)
o X
Y

7. Length of Tangent , Normal , Sub-
Tangent and Sub-Normal
X
Y
P(x,y)
Y =f(X)
G
T
o M
Let the Tangent and Normal at point p(x,y) to the Curve Y = f(X) meet the x-axis
at T and G respectively. And let PM with the ordinate through point P.

8. Here……
 PT is the Length of Tangent.
 PG is the Length of Normal.
 TM is the Length of Sub-Tangent .
MG is the Length of Sub-Normal.
1) Length of Tangent
In Triangle PMT
SinΨ = PM/PT = y/PT
PT = y/SinΨ = y CosecΨ
= y √(1+Cot²ψ)

9. Continue…….
PT = y√(1+1/tan²ψ)
= y√(1+tan²ψ)/tan²ψ
= y√{1+(dy/dx)²}/(dy/dx)
PT = y√1+(dx/dy)²
2) Length of Normal
In Triangle PMG
CosΨ = PM/PG = y/ PG

10. Continue…….
PG = y/Cosψ
PG = ySecψ
= y√(1+tan²ψ)
PG = y√1+(dx/dy)²
3) Length of Sub-Tangent
In Triangle PMT
tanψ = PM / TM
TM = y / (dy/dx)

11. 4) Length of Sub-Normal
In Triangle PMG
tan ψ = MG/ PM
Y₁ = MG/PG
MG = yy₁