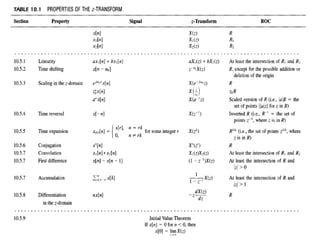
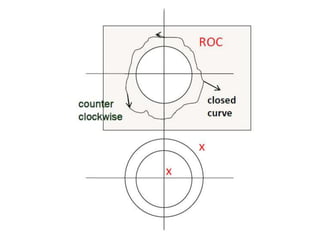
This document discusses two methods for inverse z-transforms: the convolution method and the residue method. The residue method can be used when the function is rational in the form of p/q, with unique finite poles. It involves contour integration around the origin, inside the region of convergence. The poles are the roots of the denominator polynomial. The convolution method uses the property that the inverse z-transform of two signals multiplied in the z-domain is the convolution of their inverse z-transforms.

1. Convolution and Residue Method
in Inverse Z- Transform
• Contents
i. Crux of IZT
ii. Convolution Theorem (With examples)
iii. Residue Method Integral Inversion
(With examples)

3. General Form for finding through Residue
Contour: ƶ = r.ejƜ
Contour Integration C is a counterclockwise closed contour in the ROC of X(z)
encircling the origin

5. Residue Method
• Also known as Inverse Integral Method
• The function should be rational; in form of p/q
• Unique poles to be finite
• Widely used in the analysis of quantization
errors in discrete-time systems
λk : pole
(simple)

6. • The poles {pn} are the roots of the denominator polynomial = 0.
• The poles {pn} are assumed to be distinct (no two are equal);
• Repeated roots of polynomials don’t occur in real life unless forced to.
• If X(z) is real, both poles and residues occur in complex conjugate pairs
• In case of non-simple poles; (in order of >1)
λk : pole
OR

7. Convolution Theorem/Method
• If Z-1{F (z)} = fn and Z-1{G(z)} = gn ; then ->
We tend to use
un and vn

8. •

9. • Special Thanks to Shri Shri Shri Alan
Oppenheim