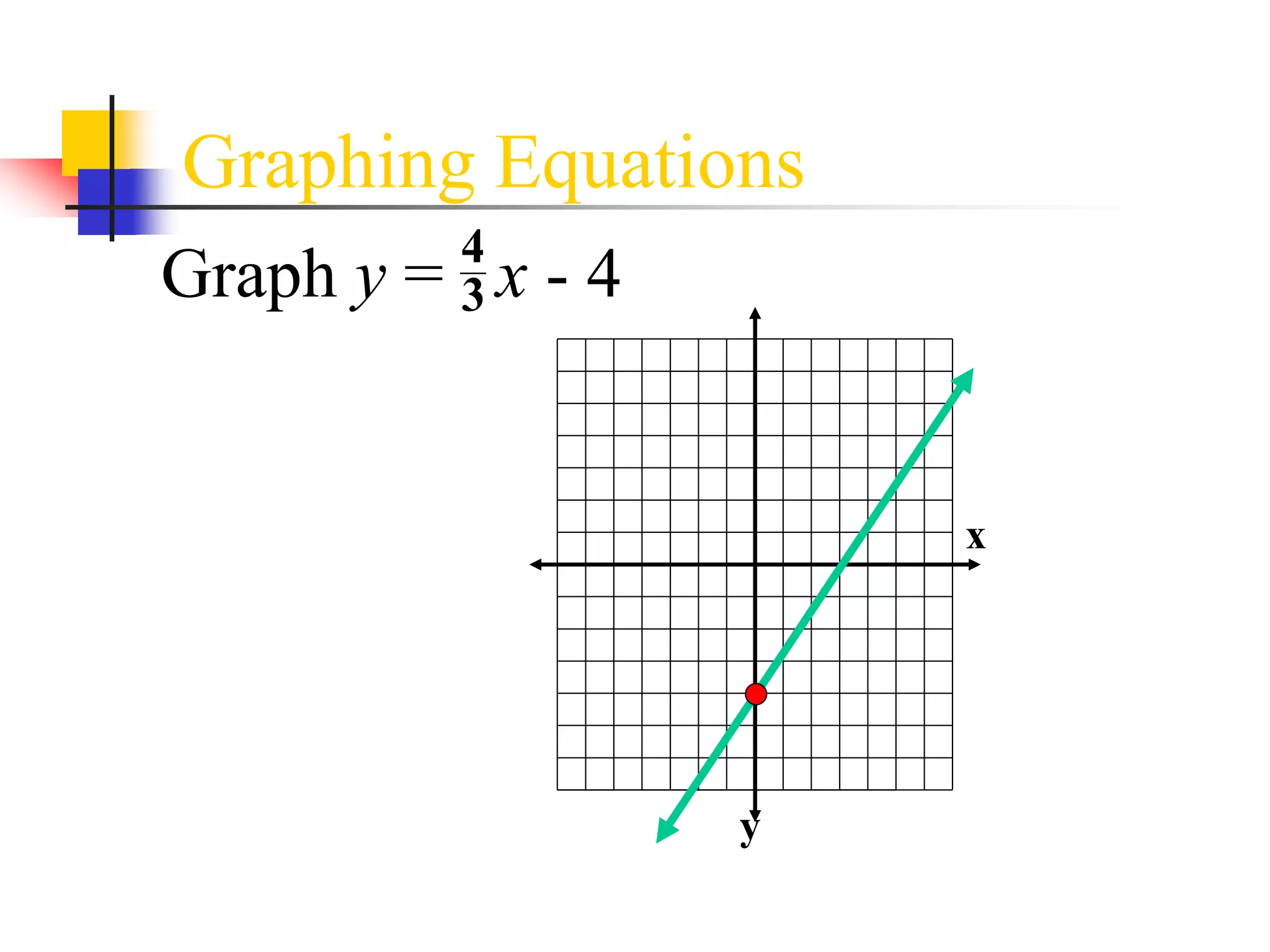
This document defines and provides examples of linear equations. It explains that a linear equation has variables with exponents of 1 that are added or subtracted. The document shows examples of linear equations in standard Ax + By = C form and identifies the slope and y-intercept. It also provides examples of nonlinear equations that do not follow the standard linear form. The document describes how to find the x-intercept and y-intercept of a linear equation by setting one variable to 0 and solving for the other. Graphing linear equations in slope-intercept form is also demonstrated.