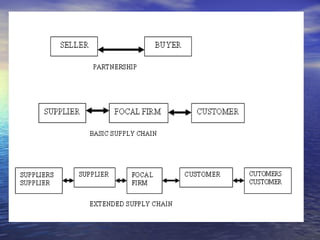
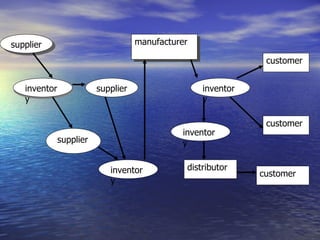
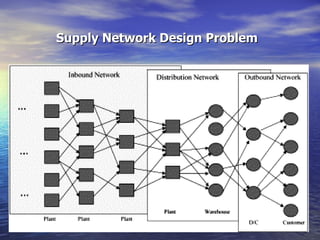
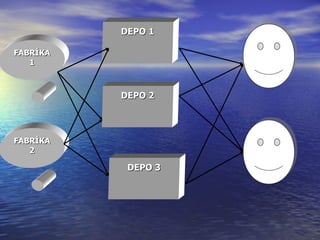
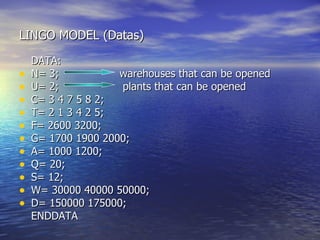
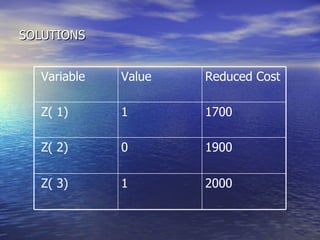
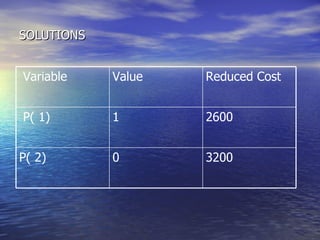
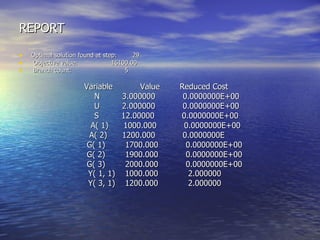
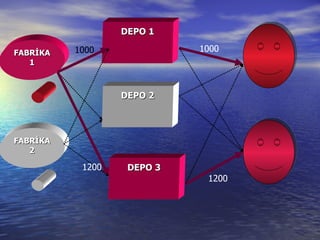
The document summarizes a mathematical model for optimizing a supply network design problem. The model determines the optimal number, location, capacity and configuration of plants, warehouses and distribution centers to meet customer demands at minimum cost. The model considers costs of transportation between facilities and fixed costs of opening facilities. The summary provides an example application of the model to a supply network with 2 plants, 3 warehouses and 2 customer zones.

1. SUPPLY CHAIN MANAGEMENT K. Özcan ATILGAN Erhan GÜL M. Onur ŞENARAS

2. TABLE OF CONTENTS What is Supply Chain Management? Types of Supply Chains The Strategic Importance of the Supply Chain Global Supply Chain Issues Vendor Selection Problems of Supply Chain Supply Network Management Supply Network Design ProblemMathematical Model Model: Distribution & Example (LINGO Solution)

3. What is Supply Chain Management? Supply chain management is the implementation of a supply chain orientation across suppliers and customers. Supply chain management is the systemic, strategic coordination of the traditional business functions within a particular company and across business within the supply chain, for the purpose of improving the long-term performance of the individual companies and the supply chain as a whole.

4. Types of Supply Chains Basic Supply Chain An Extended Supply Chain An Ultimate Supply Chain Partnership

6. THE STRATEGIC IMPORTANCE OF THE SUPPLY CHAIN As firm strive to increase their competitivenessvia product customization,high quality,cost reductions, and speed to market, they place added empahsis on the supply chain.The key to effective supply chain management is to make suppliers partners in the firm‘s strategies to satisfy an ever changing marketplace

7. supplier inventory supplier supplier inventory customer customer customer inventory inventory manufacturer distributor

8. GLOBAL SUPPLY CHAIN ISSUES Flexible enough to react to sudden changes in parts availability, distribution or shipping channels, import duties, and currency rates. Able to use the latest computer and transmission technologies to manage the shipment of parts in and finished products out. Staffed with local specialist to handle duties, trade, freight, customs, and political issues.

9. VENDOR SELECTION Vendor Evaluation Vendor Development Negotiations

10. Problems of Supply Chain Network design problem from raw material suppliers to customers. Problem of production quota assignment, by which specific quantities are distributed to each of the several facilities producing the same items. Production planning problem, considering the global BOM relationship. Global capacity planning for various manufacturing facilities in the network. Distribution planning that determines optimal distribution channel and quantity

11. Supply Network Management System * Supply network design optimization module * Production and distribution planning module * Model management module * Data management module

12. Supply Network Design Problem

13. Supply Network Design Problem The network design problem is one of the most comprehensive strategic decision problems that need to be optimized for the long-term efficient operation of whole supply chain. It determines the number, location, capacity, and types of plants, warehouses and distribution centers to be used. It also establishes distribution channels, and the amount of materials and items to consume, produce and ship from suppliers at each level to finally the customers.

14. Mathematical Model The assumptions to model are: Total capacity and operation cost of distribution centers, warehouses and manufacturing plants are known in advance. Capacity requirements of plants and warehouses for multiple products are known. Customer demands for multiple products are also known All the decisions are made within a single period. The transportation costs from facilities to facilities for each product are given

15. Input Parameters I : set of customer zones (distribution center) J : potential warehouse sites K : potential plant locations Wj : throughput limit of each warehouse site j Dk : capacity of each plant k L : set of products qkl : required capacity of the plant k for each product l ail : demand for each product l by the set of customer zone I

16. Input Parameters (Costs) Cijl : variable cost to distribute a unit of product l from an open warehouse j to a customer zone I Tjkl : variable cost to transport a unit of product l to an open warehouse j from an open plant k gj : fixed cost for each warehouse j fk : fixed cost for each plant k sjl : required throughput capacity of the warehouse j for each product l W : upper limit on the number of warehouses that can be opened P : upper limit on the number of plants that can be opened

17. Decision Variables Xijl : total number of units of product l distributed to customer zone i from open warehouse j Yjkl : total number of units of product l that is shipped to open warehouse j from open plant k Zj : indication variable whether a warehouse j is open Pk : indication variable whether a plant k is open

18. K (PLANT) J (WAREHOUSE) İ (CUSTOMERS)

19. Model: distribution Objective function:

20. Model: distribution Constraints :

21. Model: Distribution Binary Constraints: Zj ={0,1} forall j J Pk ={0,1} forall k K Xijl , Yjkl >= 0 forall i I , j J , k K and l L

22. A NUMERICAL EXAMPLE FOR THE DISTRIBUTION MODEL A product can be produced in two plants. There are 3 warehouses and 2 types of customers. We know explicitly demands of each customer. For the first customer, demand is 1000 and second is 1200. Each warehouse have throughput limits in the order of 30000, 40000, 50000. Required throughput capacity of the warehouse for our product is 12.

23. … EXAMPLE Distribution cost from an open warehouse to customers are 3, 4, 7, 5, 8, 2 ($). Fixed costs for each warehouses are 1700, 1900, 2000 ($). Fixed costs for each plants are 2600, 3200 ($). Variable costs from open plants to open warehouses are 2, 1, 3, 4, 2, 5 ($).

24. FABRİKA 1 FABRİKA 2 DEPO 1 DEPO 2 DEPO 3

25. LINGO MODEL (Sets) SETS: SETI/1..2/:I,A; SETJ/1..3/:J,G,Z,W; SETK/1..2/:P,F,D,K,Q; SETIJ(SETI,SETJ):C,X; SETJK(SETJ,SETK):T,Y; ENDSETS

26. LINGO MODEL (Datas) DATA: N= 3; warehouses that can be opened U= 2; plants that can be opened C= 3 4 7 5 8 2; T= 2 1 3 4 2 5; F= 2600 3200; G= 1700 1900 2000; A= 1000 1200; Q= 20; S= 12; W= 30000 40000 50000; D= 150000 175000; ENDDATA

27. LINGO MODEL (Constraints) MIN=@SUM(SETIJ(I,J):C(I,J)*X(I,J))+@SUM(SETJK(J,K):T(J,K)*Y(J,K))+@SUM(SETK(K):F(K)*P(K))+@SUM(SETJ(J):G(J)*Z(J)); @FOR(SETI(I):@SUM(SETJ(J):X(I,J))=A(I)); @FOR(SETJ(J):@SUM(SETI(I):S*X(I,J))<=Z(J)*W(J)); @SUM(SETJ(J):Z(J))<=N; @FOR(SETJ(J):@SUM(SETI(I):X(I,J))<=@SUM(SETK(K):Y(J,K))); @FOR(SETK(K):@SUM(SETJ(J):q(K)*Y(J,K))<=D(K)*P(K)); @SUM(SETK(K):P(K))<=U;

28. LINGO MODEL (Binary&Integer Constraints) @FOR(SETJ(J):@BIN(Z)); @FOR(SETK(K):@BIN(P)); @FOR(SETIJ(I,J):@GIN(X)); @FOR(SETJK(J,K):@GIN(Y));

29. SOLUTIONS Objective value 16100.00

30. SOLUTIONS 2.0 1200 X( 2, 3) 3.0 1000 X( 1, 1) Reduced Cost Value Variable

31. SOLUTIONS 1900 0 Z( 2) 1700 1 Z( 1) 2000 1 Z( 3) Reduced Cost Value Variable

32. SOLUTIONS Reduced Cost Value Variable 3200 0 P( 2) 2600 1 P( 1)

33. REPORT Optimal solution found at step: 29 Objective value: 16100.00 Branch count: 5 Variable Value Reduced Cost N 3.000000 0.0000000E+00 U 2.000000 0.0000000E+00 S 12.00000 0.0000000E+00 A( 1) 1000.000 0.0000000E+00 A( 2) 1200.000 0.0000000E G( 1) 1700.000 0.0000000E+00 G( 2) 1900.000 0.0000000E+00 G( 3) 2000.000 0.0000000E+00 Y( 1, 1) 1000.000 2.000000 Y( 3, 1) 1200.000 2.000000

34. 1000 1200 1000 1200 FABRİKA 1 FABRİKA 2 DEPO 1 DEPO 2 DEPO 3

35. TEŞEKKÜRLER…