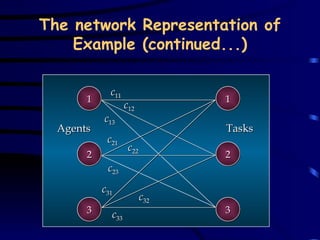
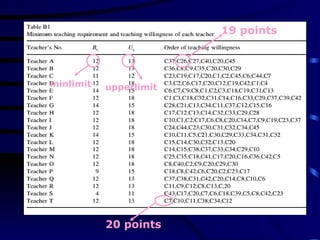
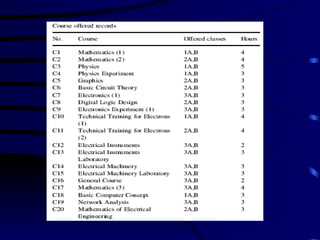
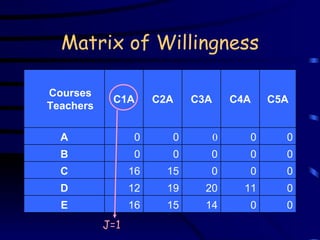
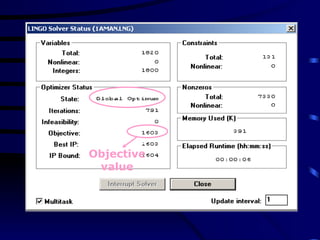
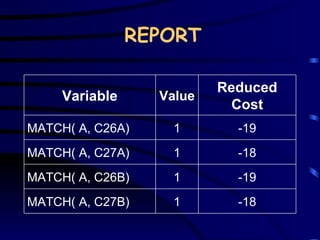
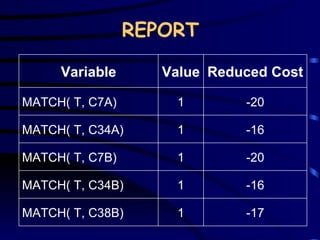
The document discusses assignment problems and their applications. It provides examples of assignment problems involving assigning workers to jobs or tasks. The goal is typically to minimize costs or maximize satisfaction. The document then summarizes a research article that uses a genetic algorithm to solve the specific problem of optimally assigning teachers to courses while considering various constraints.

1. Assignment Problems Hazırlayanlar: Ali Evren Erdin Arzu Çalık Hilal Demirhan

7. The network Representation of Example (continued...) 2 3 1 2 3 1 c 11 c 12 c 13 c 21 c 22 c 23 c 31 c 32 c 33 Agents Tasks

9. “ An Application of Genetic Algorithm Methods for Teacher Assignment Problems” The ARTICLE

14. The Questionnarie

15. 20 points 19 points minlimit upperlimit

18. The objection function for the problem will be :

20. The Lingo Formulation

21. SETS : teachers / A B C D E F G H I J K L M N O P Q R S T /: upperlimit, minlimit; c ourses / C1A C2A .................... C45A C1B C2B .................... C45B /: hours; chromosomes ( teachers, courses ) : willingness, match; ENDSETS

22. DATA: willingness = (The matrix taken from the given table B1 ) hours = 4 4 5 3 3 3 3 3 3 4 4 2 3 3 3 2 4 3 3 3 3 3 3 3 3 3 3 3 2 3 3 3 2 2 3 3 3 3 3 3 3 2 3 3 3 4 4 5 3 3 3 3 3 3 4 4 2 3 3 3 2 4 3 3 3 3 3 3 3 3 3 3 3 2 3 3 3 2 2 3 3 3 3 3 3 3 2 3 3 3; minlimit = 12 12 11 12 14 12 14 12 12 12 14 12 12 12 12 9 12 12 4 12; upperlimit = 13 13 12 18 15 18 15 18 18 18 15 18 18 18 18 15 13 13 11 13; ENDDATA

23. Matrix of Willingness J=1 0 0 14 15 16 E 0 11 20 19 12 D 0 0 0 15 16 C 0 0 0 0 0 B 0 0 0 0 0 A C5A C4A C3A C2A C1A Courses Teachers

27. Objective value

28. REPORT -18 1 MATCH( A, C27B) -19 1 MATCH( A, C26B) -18 1 MATCH( A, C27A) -19 1 MATCH( A, C26A) Reduced Cost Value Variable

31. REPORT -17 1 MATCH( T, C38B) -16 1 MATCH( T, C34B) -20 1 MATCH( T, C7B) -16 1 MATCH( T, C34A) -20 1 MATCH( T, C7A) Reduced Cost Value Variable

32. THANKS!