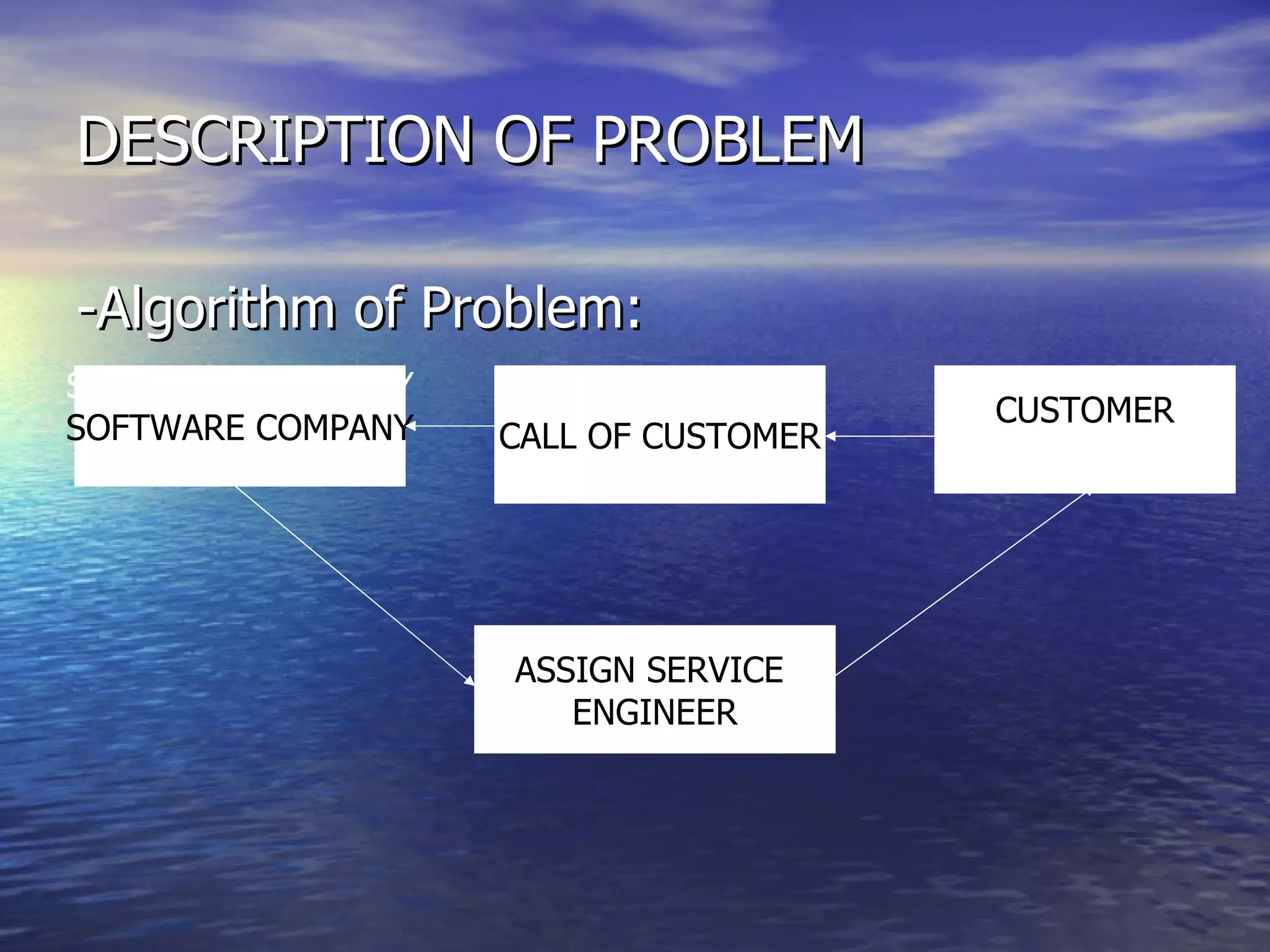
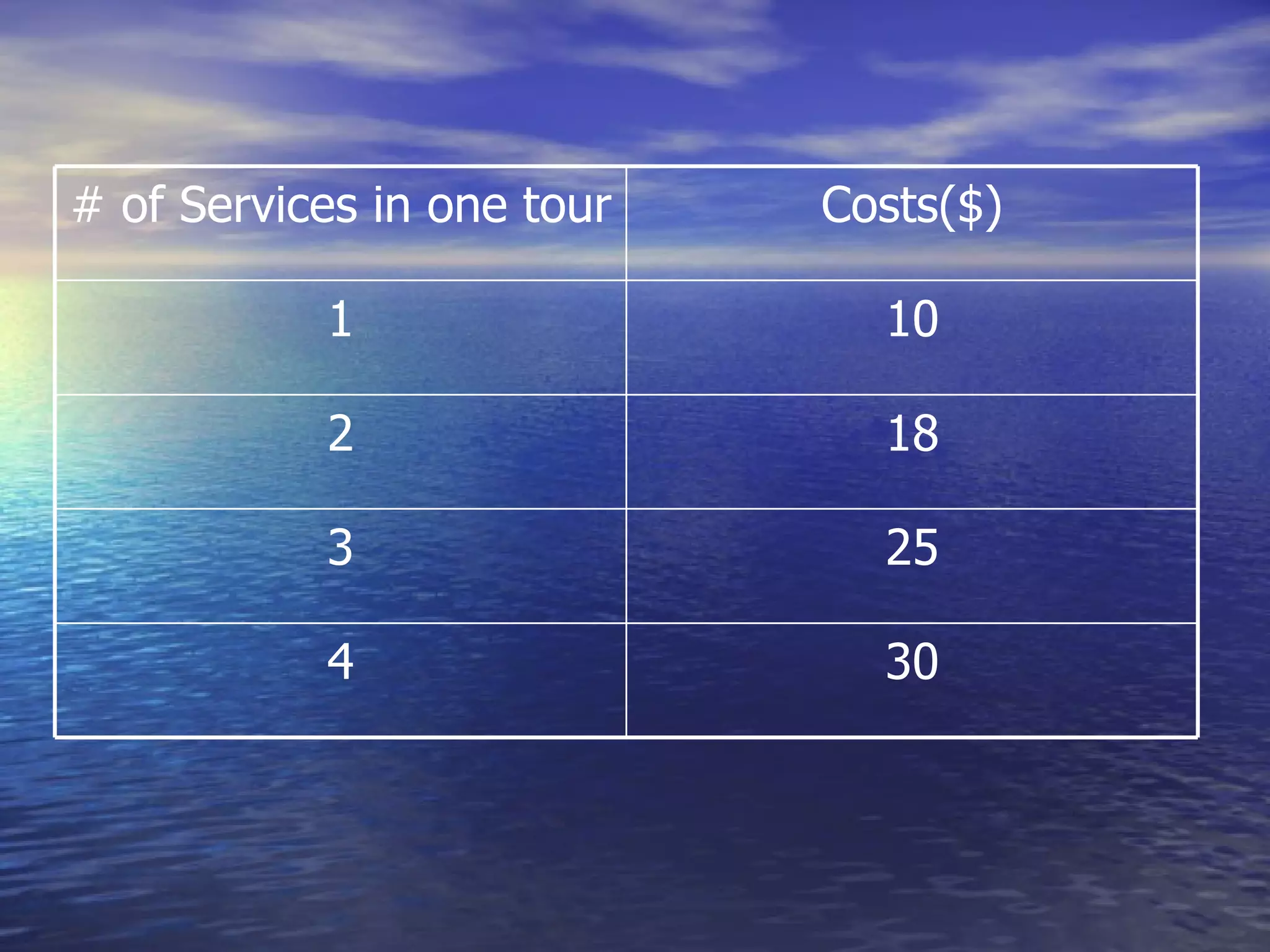
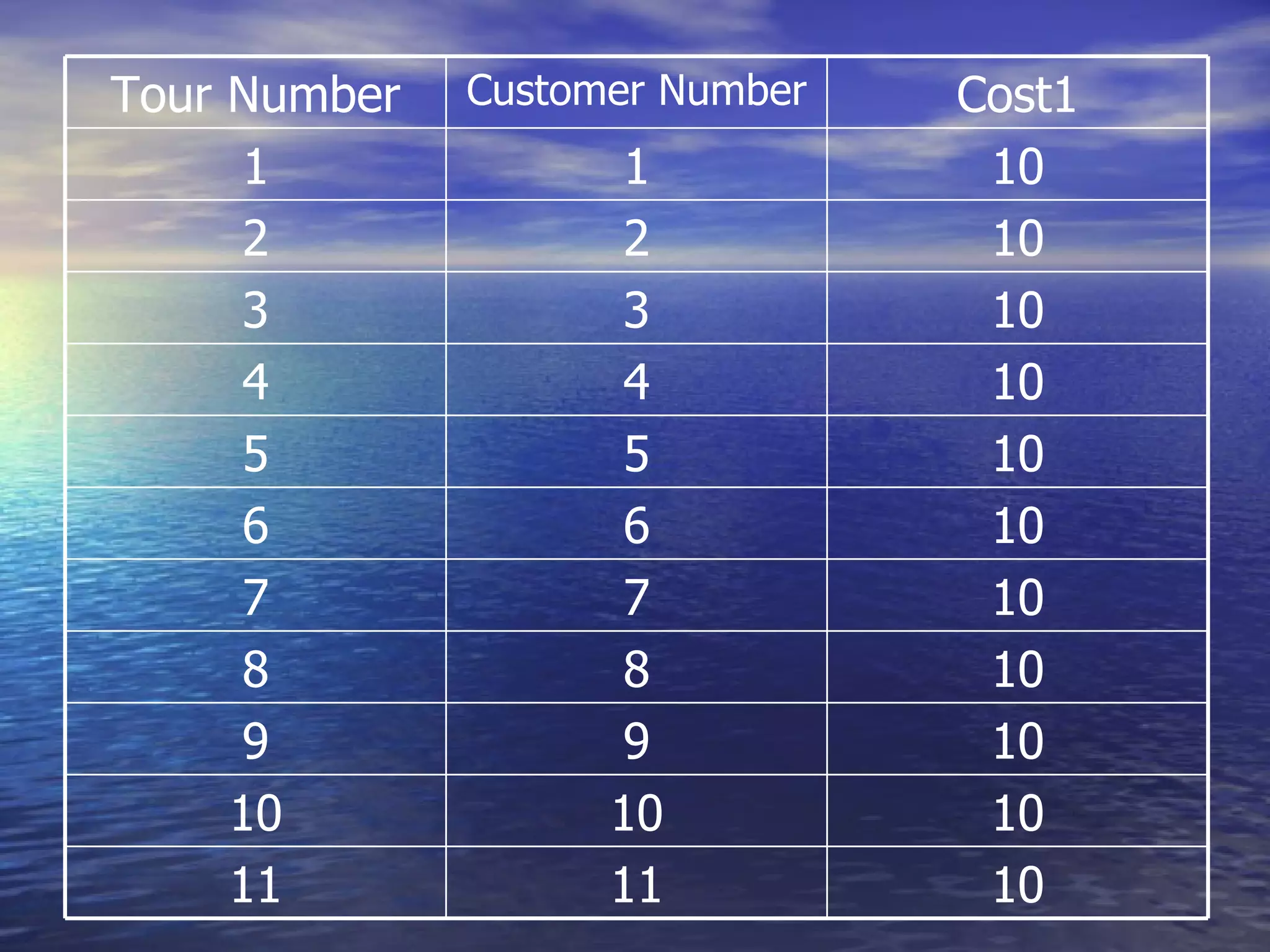
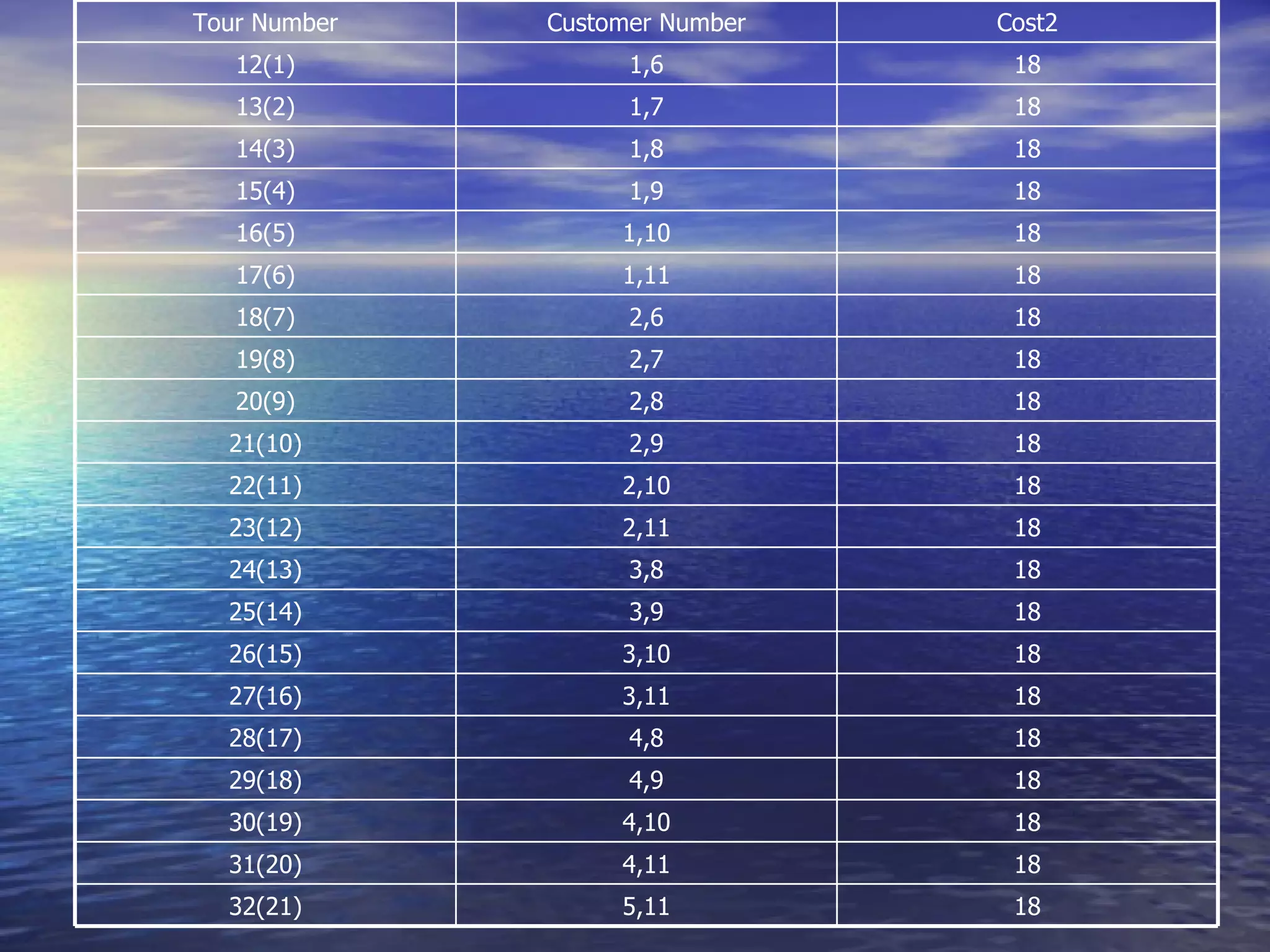
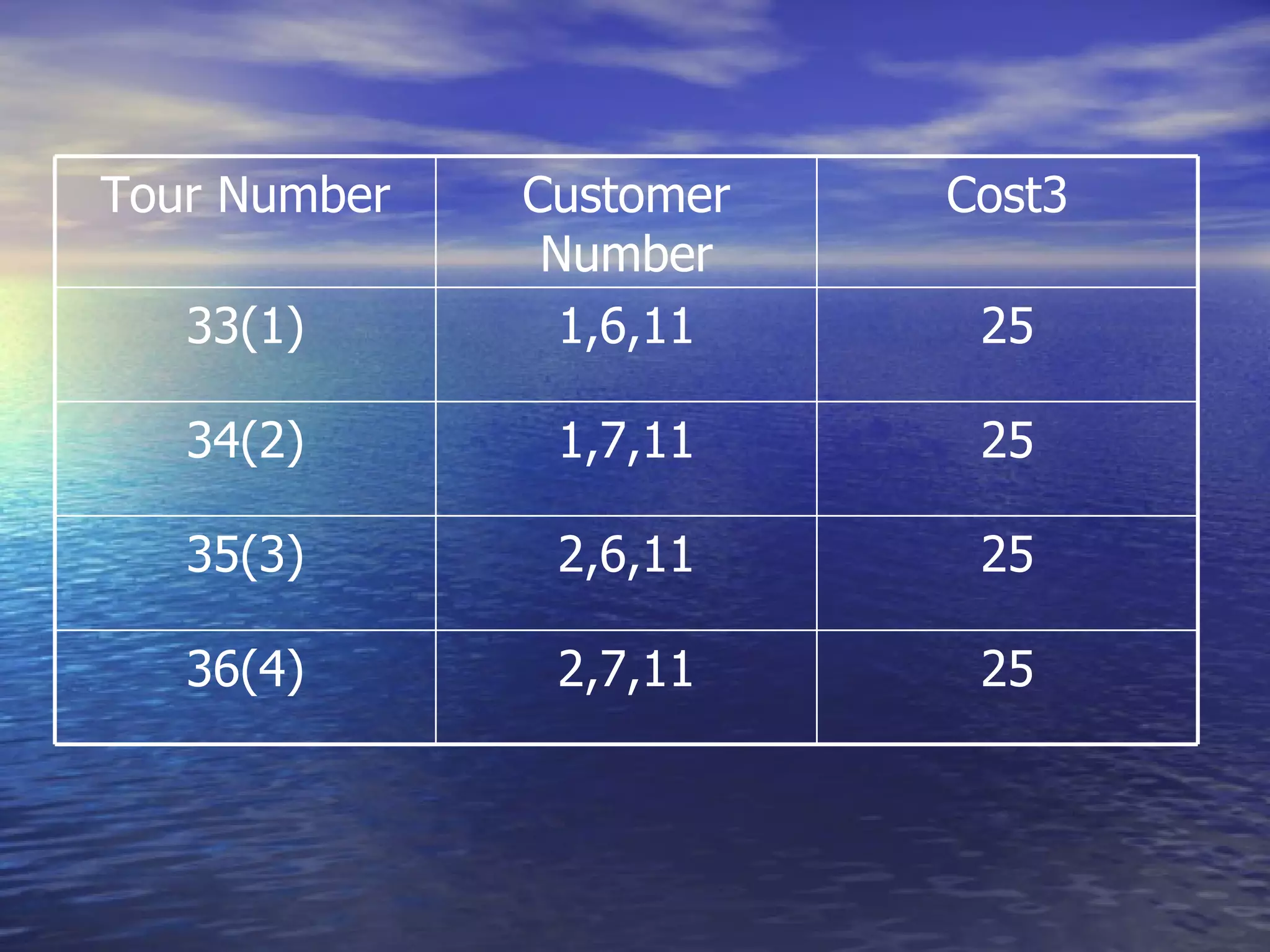
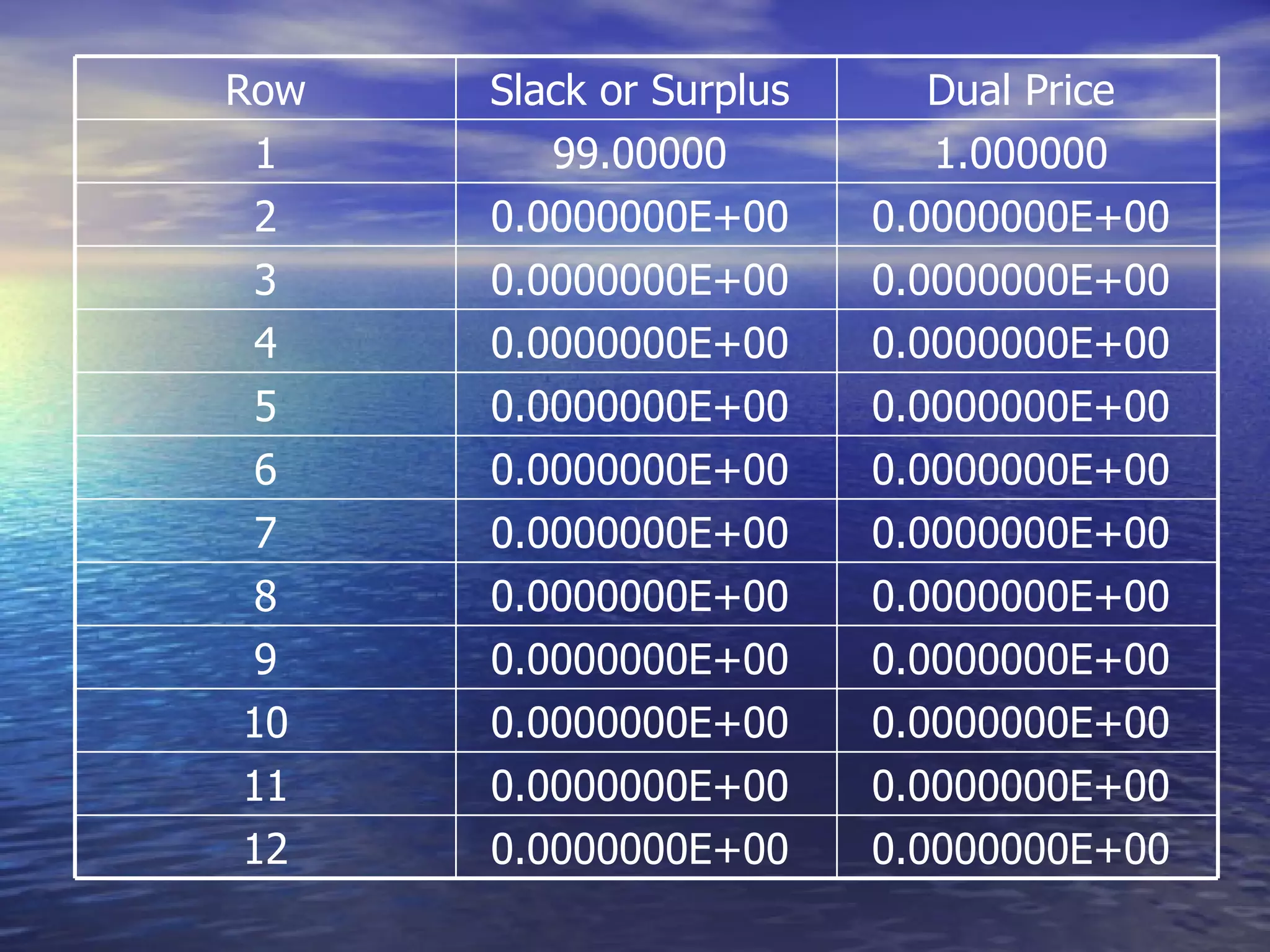
The document discusses crew scheduling and provides a mathematical model for optimizing service engineer assignments. It describes the problem of assigning 11 service engineers to customer calls between 1pm-5pm in a way that minimizes costs. A linear program is formulated in Lingo with decision variables to represent single, double and triple customer assignments. The model is solved, finding an optimal solution with a cost of $99 assigning specific engineers to individual and grouped customer calls.

1. CREW SCHEDULING İ.HAKAN KARAÇİZMELİ

2. GENERAL VIEW CREW SCHEDULING TYPES FLEXIBLE MANAGEMENT STRATEGIES DESCRIPTION OF PROBLEM FORMULATION OF PROBLEM MODEL IN LINGO SOLUTION & ANALYSIS

3. CREW SCHEDULING Airline Crew Scheduling 1. The most appropriate pairings. 2.Equal workloads. 3.Minimum crew COSTS. Mass Transit Crew Scheduling 1. Railway track maintenance problems. 2.Mathematical program. 3.Tabu search.

4. Generic Crew Scheduling 1. Manpower scheduling problems. 2.Mixed integer program. 3.Mimimum manpower. 4.Package programs(CPLEX..).

5. FLEXIBLE MANAGEMENT STRATEGIES Functional Flexibility - Deployment on different tasks. Numerical Flexibility - Variable working hours. Temporal Flexibility - Career breaks,job sharing,term-time works.. Wage Flexibility - Performance related pays.

6. DESCRIPTION OF PROBLEM -Algorithm of Problem: SOFTWARE COMPANY SOFTWARE COMPANY CUSTOMER CALL OF CUSTOMER CALL OF CUSTOMER ASSIGN SERVICE ENGINEER

7. Informations about problem Service engineering is not different job . All of Software engineers may go services . Service time includes times which pass on the way too . We see that service times did not pass over 2 hours according to old datas . This problem include assignments only for an afternoon .

8. 17:00 11 16:00 10 16:00 9 16:00 8 15:00 7 15:00 6 14:30 5 14:00 4 14:00 3 13:00 2 13:00 1 Time of Appointment Customer Number

9. 30 4 25 3 18 2 10 1 Costs($) # of Services in one tour

10. 10 11 11 10 10 10 10 9 9 10 8 8 10 7 7 10 6 6 10 5 5 10 4 4 10 3 3 10 2 2 10 1 1 Cost1 Customer Number Tour Number

11. 18 5,11 32(21) 18 4,11 31(20) 18 4,10 30(19) 18 4,9 29(18) 18 4,8 28(17) 18 3,11 27(16) 18 3,10 26(15) 18 3,9 25(14) 18 3,8 24(13) 18 2,11 23(12) 18 2,10 22(11) 18 2,9 21(10) 18 2,8 20(9) 18 2,7 19(8) 18 2,6 18(7) 18 1,11 17(6) 18 1,10 16(5) 18 1,9 15(4) 18 1,8 14(3) 18 1,7 13(2) 18 1,6 12(1) Cost2 Customer Number Tour Number

12. 25 2,7,11 36(4) 25 2,6,11 35(3) 25 1,7,11 34(2) 25 1,6,11 33(1) Cost3 Customer Number Tour Number

13. After these informations we describe our mathematical model: Decison Variables : -X : Number of 1 Customer Service in One Tour ( X=1..11 ) -Y : Number of 2 Customer Services in One Tour ( Y=1..21 ) -Z : Number of 3 Customer Services in One Tour ( Z=1..4 )

14. Objective Function: -Zmin=∑(X*Cost1) + ∑(Y*Cost2) + ∑(Z*Cost3)

15. Constraints: For customer 1 : X1 + Y1 + Y2 + Y3 + Y4 +Y5 + Y6 + Z1 + Z2 = 1 For customer 2 : X2 + Y7 + Y8 + Y9 + Y10 + Y11 + Y12 + Z3 + Z4 = 1 For customer 3 : X3 + Y13 + Y14 + Y15 + Y16 = 1 For customer 4 : X4 + Y17 + Y18 + Y19 + Y20 = 1 For customer 5 : X5 + Y21 = 1 For customer 6 : X6 + Y1 + Y7 + Z1 + Z3 = 1 For customer 7 : X7 + Y2 + Y8 + Z2 + Z4 = 1 For customer 8 : X8 + Y3 + Y9 + Y13 + Y17 = 1 For customer 9 : X9 + Y4 + Y10 + Y14 + Y18 = 1 For customer10: X10 + Y5 + Y11 + Y15 + Y19 = 1 For customer11: X11 + Y6 + Y12 + Y16 + Y20 + Y21 + Z1 + Z2 + Z3 + Z4=1

16. MODEL IN LINGO SETS: SERVICE/1..11/:COST1,X; SERVICE2/1..21/:COST2,Y; LOOK(SERVICE,SERVICE2):MATRIX1; SERVICE3/1..4/:COST3,Z; LOOK2(SERVICE,SERVICE3):MATRIX2; ENDSETS

17. DATA: COST1=10 10 10 10 10 10 10 10 10 10 10; MATRIX1=1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 1 0 0 0 1 1;

18. COST2=18 18 18 18 18 18 18 18 18 18 18 18 18 18 18 18 18 18 18 18 18; MATRIX2=1 1 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1; COST3=25 25 25 25; ENDDATA

19. @FOR(SERVICE:@BIN(X)); @FOR(SERVICE2:@BIN(Y)); @FOR(SERVICE3:@BIN(Z)); MIN =@SUM(SERVICE:X*COST1)+@SUM(SERVICE2:Y*COST2)+@SUM (SERVICE3:Z*COST3); @FOR(SERVICE(I):X(I)+@SUM(SERVICE2(J):MATRIX1(I,J)*Y(J))+@SUM(SERVICE3(K):MATRIX2(I,K)*Z(K)) = 1); END

20. SOLUTION & ANALYSIS Objective Value = 99 $ X5 = 1 X10 = 1 Y1 = 1 Y14 = 1 Y17 = 1 Z4 = 1

21. X5 CUSTOMER5 at 14:30 X10 CUSTOMER10 at 16:00 Y1 CUSTOMER1 at 13:00 CUSTOMER6 at 15:00 Y14 CUSTOMER3 at 14:00 CUSTOMER9 at 16:00

22. Y17 CUSTOMER4 at 14:00 CUSTOMER8 at 16:00 Z4 CUSTOMER2 at 13:00 CUSTOMER7 at 15:00 CUSTOMER11 at 17:00

23. Objective Value=1*10+1*10+1*18+1*18+1*18+1*25=99

24. 0.0000000E+00 0.0000000E+00 12 0.0000000E+00 0.0000000E+00 11 0.0000000E+00 0.0000000E+00 10 0.0000000E+00 0.0000000E+00 9 0.0000000E+00 0.0000000E+00 8 0.0000000E+00 0.0000000E+00 7 0.0000000E+00 0.0000000E+00 6 0.0000000E+00 0.0000000E+00 5 0.0000000E+00 0.0000000E+00 4 0.0000000E+00 0.0000000E+00 3 0.0000000E+00 0.0000000E+00 2 1.000000 99.00000 1 Dual Price Slack or Surplus Row

25. THANK YOU