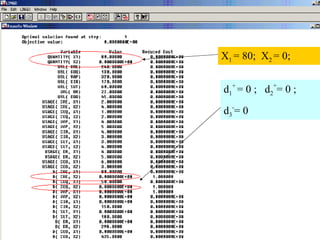
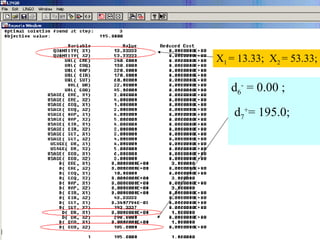
The document discusses goal programming and its application to a case study of a medical manufacturing company. It introduces goal programming and describes how it can address multiple goals through deviations from target values. The case study establishes strategic, intermediate, and tactical goals for two medical products related to engineering cost, quality cost, production cost, setup time, delivery reliability and operations cost. A goal programming model is constructed to minimize deviations from these goals. The model is solved in steps to find optimal values for the decision variables to meet the goals.

1. GOAL PROGRAMMING Serhat ÖKSÜZ Ahmet TATIŞ Mehmet YILMAZ

2. THE VIEW OF THE PRESENTATION ● Introduction ● System approach to concurrent engineering ● Goal Programming ● Application Areas ● Weighting Method and Preemptive Method ● The Case Study and The Example ● Demonstration of The Model By Using Sets ● Managerial implications for the company ● Conclusions and assessment

3. INTRODUCTION ● Life-Cycle Costing (LCC) ; ● Time-Based Competition (TBC) ; ● T he three planning-horizon levels ; ▪ S trategic, ▪ I ntermediate , ▪ T actical ,

4. Concurrent Engineering Is the collaboration among functional areas; Product design ,design for quality ,process design, design for manufacturing and planning ,logistic design etc. In the early phases of product design CE requires : ▪ fast adaptation ▪ product innovation ▪ short product delivery time to market for a firm to remain competitive . ▪

6. GOAL PROGRAMMING Introduced by Charnes and Cooper in 1960’s Provides a method of dealing with a collection of goals, rather than an explicit objective function. Objective is to minimize the deviation from each of the goals that have been established. Constraints are “soft” in that you may violate one (i.e. not meet one goal) if it means you can make better progress toward one of the other goals.

7. Goal Programming Versus Linear Programming Multiple Goals (instead of one goal) Deviational Variables Minimized (instead of maximizing profit or minimizing cost of LP) “ Satisficing ” (instead of optimizing)

8. APPLICATION AREAS Accounting Agriculture Economics Engineering Finance Government I nternational Context Management Marketing

9. Types Of Goal Programming 􀂅 Weights method: the single objective function is the weighted sum of the of the functions representing the goals of the problem. MIN Z= w 1 d 1 +w 2 d 2 +…+w n d n 􀂅 Preemptive method: prioritizes the goals in order of importance, then optimizes one goal at a time.

10. CASE STUDY AND THE EXAMPLE COMPANY PROFILE ▪ Medical manufacturing company producing skin prepping applicators ▪ 10 years in the Industry ▪ Hospitals, first aid users and indust rial companies are the customers ▪ 125 employees ▪ 17 million $ annual sales

11. Aim of the study Minimized life cycle cost and time Timely introduction of products to market Increased deliver reliability Measurable improvement in supplier performance Improvements in changeover and setup technologies

12. CE TEAM Product designer Manufacturing engineer Quality control manager Marketing manager Purchasing manager Product design activities and practices are coordinated and accomplished concurrently. Suppliers inputs and assistance is in terms of part and product is taken into consideration.

13. STRATEGIC GOALS (P 1 ) COST OF PRODUDUCTS TO MARKET (P 11 ) TIME OF PRODUDUCTS TO MARKET (P 12 ) ▪ Products research and development cost ▪ Engineering design cost ▪ Product investment cost ▪ Product investment and developing cost ▪ Cost of quality ▪ Speed of response to customers ▪ Product time to market ▪ Design lead time ▪ Order-to-delivery cycle ▪ Total product delivery time

14. INTERMEDIATE GOALS (P 2 ) THROUGHPUT COST (P 21 ) THROUGHPUT TIME (P 22 ) ▪ Procurement cost ▪ Non-recurring manufacturing costs ▪ Recurring manufacturing costs ▪ Facilities cost ▪ Initial logistics/support costs ▪ Cost of quality ▪ Manufacturing lead time ▪ Set-up time ▪ Producrtion cycle time ▪ Changeover time ▪ Delay time ▪ Distribution lead time ▪ Manufacturing response time ▪ Procurement lead time

15. TACTICAL GOALS (P 3 ) OPERATIONAL AND MATERIAL COST (P 31 ) DELIVERY TIMES (P 32 ) ▪ Operations cost ▪ Maintenance cost ▪ Product modification cost ▪ Facilities cost ▪ Product phase-out and disposal cost ▪ Delivery reliability ▪ Delivery speed

17. THE GOALS OF THE COMPANY For products X 1 and X 2 ; STRATEGIC GOALS ▪ Engineering Des i gn Cost under 240 $ ▪ Cost Of Quality under 130 $ ▪ Minimum Value Added to Product 320 $ INTERMED I ATE GOALS ▪ Recurring manufacturing cost under 170 $ ▪ Set up Time under 60 min TACTICAL GOALS ▪ Delivery Reliability over 22 ▪ Operation Cost under 45 $

18. Strategic Goal Engineering Design Cost Total EDC : 2 x 1 + 4 x 2 Upper Resource Limit : 240 2 x 1 + 4 x 2 = 240 + d 1 + - d 1 - 2 x 1 + 4 x 2 + d 1 - - d 1 + = 240 { 2 x 1 + 4 x 2 < = 240 } d 1 + indicates the EDC over 240 while d 1 - indicates the EDC under the goal . The objective is to minimize d 1 +

19. Strategic Goal Cost of Quality Total COQ : 1 x 1 + 2 x 2 Upper Resource Limit : 130 1 x 1 + 2 x 2 = 130 + d 2 + - d 2 - 1 x 1 + 2 x 2 + d 2 - - d 2 + = 130 { 1 x 1 + 2 x 2 < = 130 } d 2 + indicates the COQ over 130 while d 2 - indicates the COQ under the goal . The objective is to minimize d 2 +

20. Strategic Goal Value Added to Product Total VAP : 4 x 1 + 5 x 2 Upper Resource Limit : 320 4 x 1 + 5 x 2 = 320 + d 3 + - d 3 - 4 x 1 + 5 x 2 + d 3 - - d 3 + = 320 { 4 x 1 + 5 x 2 > = 320 } d 3 + indicates the VAP over 320 while d 3 - indicates the VAP under the goal . The objective is to minimize d 3 -

21. I ntermediate Goal Recurring Manufacturing Cost Total RMC : 4 x 1 + 3 x 2 Upper Resource Limit : 170 4 x 1 + 3 x 2 = 170 + d 4 + - d 4 - 4 x 1 + 3 x 2 + d 4 - - d 4 + = 170 { 4 x 1 + 3 x 2 < = 170 } d 4 + indicates the RMC over 170 while d 4 - indicates the RMC under the goal . The objective is to minimize d 4 +

22. I ntermediate Goal Set-Up Time Total SUT : 3 x 1 + 4 x 2 Upper Resource Limit : 60 3 x 1 + 4 x 2 = 60 + d 5 + - d 5 - 3 x 1 + 4 x 2 + d 5 - - d 5 + = 60 { 3 x 1 + 4 x 2 < = 60 } d 5 + indicates the SUT over 60 while d 5 - indicates the SUT under the goal . The objective is to minimize d 5 +

23. Tactical Goal Delivery Reliability Total DR : 3 x 1 + 4 x 2 Upper Resource Limit : 22 4 x 1 + 5 x 2 = 22 + d 6 + - d 6 - 4 x 1 + 5 x 2 + d 6 - - d 6 + = 22 { 4 x 1 + 5 x 2 > = 22 } d 6 + indicates the DR over 22 while d 6 - indicates the DR under the goal . The objective is to minimize d 6 -

24. Tactical Goal Operations Cost Total OC : 3 x 1 + 4 x 2 Upper Resource Limit : 45 6 x 1 + 3 x 2 = 45 + d 7 + - d 7 - 6 x 1 + 3 x 2 + d 7 - - d 7 + = 45 { 6 x 1 + 3 x 2 < = 45 } d 7 + indicates the OC over 45 while d 7 - indicates the OC under the goal . The objective is to minimize d 7 +

25. The Model

26. The Model The strategic goal : Min d 1 + + d 2 + + d 3 - ; { Min w 1 d 1 + +w 1 d 2 + +w 1 d 3 - + w 2 d 4 + +w 2 d 5 + + w 3 d 6 - + w 3 d 7 + } 2 x 1 + 4 x 2 + d 1 - - d 1 + = 240 ; 1 x 1 + 2 x 2 + d 2 - - d 2 + = 130 ; 4 x 1 + 5 x 2 + d 3 - - d 3 + = 320 ; 4 x 1 + 3 x 2 + d 4 - - d 4 + = 170 ; 3 x 1 + 4 x 2 + d 5 - - d 5 + = 60 ; 4 x 1 + 5 x 2 + d 6 - - d 6 + = 22 ; 6 x 1 + 3 x 2 + d 7 - - d 7 + = 45 ; x 1 , x 2 , d i + , d i -  0

27. The solution Let the solution be: x 1 = 80 , x 2 = 0 , d 1 + =0 , d 2 + = 0 , d 3 - =0

28. The Model The intermediate goal : Min d 4 + + d 5 + ; 2 x 1 + 4 x 2 + d 1 - - d 1 + = 240 ; 1 x 1 + 2 x 2 + d 2 - - d 2 + = 130 ; 4 x 1 + 5 x 2 + d 3 - - d 3 + = 320 ; 4 x 1 + 3 x 2 + d 4 - - d 4 + = 170 ; 3 x 1 + 4 x 2 + d 5 - - d 5 + = 60 ; 4 x 1 + 5 x 2 + d 6 - - d 6 + = 22 ; 6 x 1 + 3 x 2 + d 7 - - d 7 + = 45 ; d 1 + =0 ; d 2 + = 0 ; d 3 - = 0 ;

29. The solution Let the solution be: x 1 = 13.33 , x 2 = 53.33 , d 4 + = 43.33 , d 5 + = 193.33

30. The Model The tactical goal : Min d 6 - + d 7 + ; 2 x 1 + 4 x 2 + d 1 - - d 1 + = 240 ; 1 x 1 + 2 x 2 + d 2 - - d 2 + = 130 ; 4 x 1 + 5 x 2 + d 3 - - d 3 + = 320 ; 4 x 1 + 3 x 2 + d 4 - - d 4 + = 170 ; 3 x 1 + 4 x 2 + d 5 - - d 5 + = 60 ; 4 x 1 + 5 x 2 + d 6 - - d 6 + = 22 ; 6 x 1 + 3 x 2 + d 7 - - d 7 + = 45 ; d 1 + =0 ; d 2 + = 0 ; d 3 - = 0 ; d 4 + = 43.33 ; d 5 + = 193.33 ;

31. The solution Let the solution be: x 1 = 13.33 , x 2 = 53.33 , (EDC) d 1 + = 0 & d 1 - = 0 , (COQ) d 2 + = 0 & d 2 - = 10 , (VAP) d 3 + = 0 & d 3 - =0 , (RMC) d 4 + = 43.3 & d 4 - =0 , (SUT) d 5 + = 193.3 & d 5 - =0 , (DR) d 6 + = 298 & d 6 - = 0 , (OC) d 7 + = 195 & d 7 - =0 .

32. The solution Let the solution be: This means: EDC = 2 x 1 + 4 x 2 + d 1 - - d 1 + = 240 ; COQ = 1 x 1 + 2 x 2 - d 2 + = 130 – 10 = 120 ; VAP = 4 x 1 + 5 x 2 + d 3 - - d 3 + = 320 ; RMC = 4 x 1 + 3 x 2 + d 4 - = 170 + 43.3 = 213.3 ; SUT = 3 x 1 + 4 x 2 + d 5 - = 60 +193.33 = 253.33 ; DR = 4 x 1 + 5 x 2 + d 6 - = 22 + 298 = 320 ; OC = 6 x 1 + 3 x 2 + d 7 - = 45 + 195 = 240 .

33. Min d 1 + + d 2 + + d 3 - 2 x 1 + 4 x 2 + d 1 - - d 1 + = 240 1 x 1 + 2 x 2 + d 2 - - d 2 + = 130 4 x 1 + 5 x 2 + d 3 - - d 3 + = 320 4 x 1 + 3 x 2 + d 4 - - d 4 + = 170 3 x 1 + 4 x 2 + d 5 - - d 5 + = 60 4 x 1 + 5 x 2 + d 6 - - d 6 + = 22 6 x 1 + 3 x 2 + d 7 - - d 7 + = 45

34. X 1 = 80; X 2 = 0; d 1 + = 0 ; d 2 + = 0 ; d 3 - = 0

35. Min d 4 + + d 5 + 2 x 1 + 4 x 2 + d 1 - - d 1 + = 240 1 x 1 + 2 x 2 + d 2 - - d 2 + = 130 4 x 1 + 5 x 2 + d 3 - - d 3 + = 320 4 x 1 + 3 x 2 + d 4 - - d 4 + = 170 3 x 1 + 4 x 2 + d 5 - - d 5 + = 60 4 x 1 + 5 x 2 + d 6 - - d 6 + = 22 6 x 1 + 3 x 2 + d 7 - - d 7 + = 45 d 1 + + d 2 + + d 3 - = 0

36. X 1 = 13.33; X 2 = 53.33; d 4 + = 43.33 ; d 5 + = 193.33;

37. Min d 6 - + d 7 + 2 x 1 + 4 x 2 + d 1 - - d 1 + = 240 1 x 1 + 2 x 2 + d 2 - - d 2 + = 130 4 x 1 + 5 x 2 + d 3 - - d 3 + = 320 4 x 1 + 3 x 2 + d 4 - - d 4 + = 170 3 x 1 + 4 x 2 + d 5 - - d 5 + = 60 4 x 1 + 5 x 2 + d 6 - - d 6 + = 22 6 x 1 + 3 x 2 + d 7 - - d 7 + = 45 d 1 + + d 2 + + d 3 - = 0 d 4 + +d 5 + = 236.667;

38. X 1 = 13.33; X 2 = 53.33; d 6 - = 0.00 ; d 7 + = 195.0;

39. CONCLUSION PGP is particularly appropriate where there is a hierarchy of priority levels for the goals, as is the case in this paper The most important decisions with regard to time and cost of products are made at the product design stage Using CE optimises the LCC and TBC in order to be competitive

40. THANKS