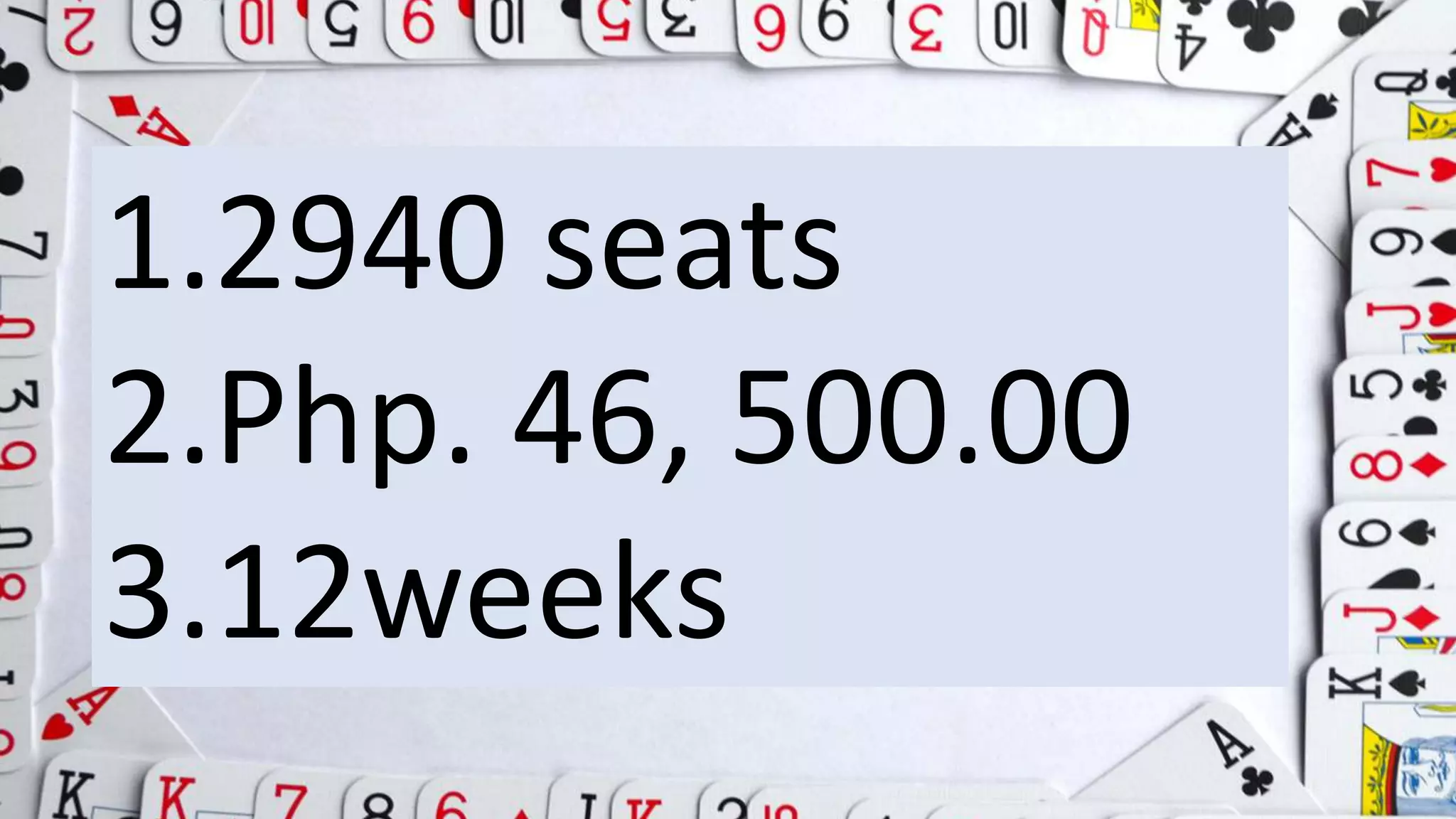
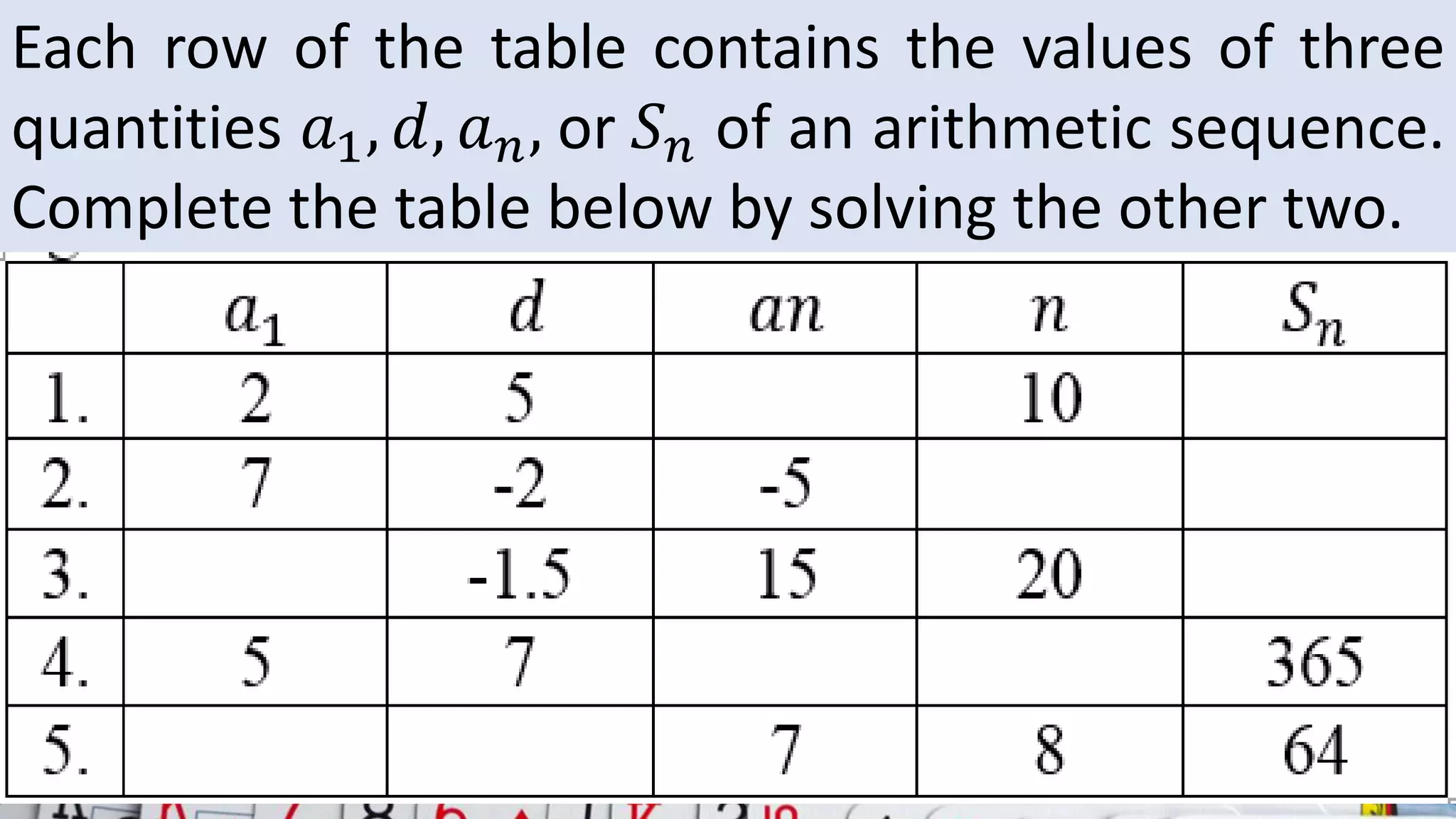
Here are the steps to solve the problems: 1. Given: a1 = 15 seats, d = 3 additional seats per row, n = 40 rows Solve for an: an = a1 + (n-1)d = 15 + (40-1)3 = 15 + 117 = 132 Solve for S40: S40 = n/2(a1 + an) = 40/2(15 + 132) = 40/2(147) = 2940 2. Given: a1 = Php 1000, d = Php 300 additional sales per week, n = 15 weeks Solve for an: an = a1 +

2. What can be
seen once in a
minute, twice in
a moment, and
never in a
thousand year?
START TIMERTIME’S UP!

3. Which tire doesn’t
move when a car
turns right?
START TIMERTIME’S UP!

4. People buy me to
eat, but never eat
me. What am I?
START TIMERTIME’S UP!

5. 1. Form a pyramid of cans or coins with 5 cans in the
first row.
2. Place one (1) fewer cans or coins in each successive
row thereafter.
3. After forming the pyramid, how many rows does the
pyramid have?
4. How many cans or coins are there in each rows? Does
the number of cans or coins in each row form an
arithmetic sequence?
5. How many total cans are there in the pyramid?

6. Sum of Arithmetic
Sequence
Arithmetic Sequence

7. 1. Find the sum of the first 20 terms of the arithmetic
sequence 15, 19, 23, 27, …
Solution 1:
We first find 𝑎20 by substituting 𝑎1 = 15,
𝑑 = 4 and 𝑛 = 20 in the formula
𝑎 𝑛 = 𝑎1 + (𝑛 − 1)𝑑
𝑎20 = 15 + (20 − 1)4
𝑎20 = 15 + (19)4
𝑎20 = 15 + 76
𝑎20 = 91

8. Solving for 𝑆20, we substitute 𝑛 = 20, 𝑎1 = 15
and 𝑎 𝑛 = 91 in the formula
𝑆 𝑛 =
𝑛
2
(𝑎1 + 𝑎 𝑛 )
𝑆20 =
20
2
(15 + 91)
𝑆20 =
20
2
(106)
𝑆20 = 10 (106)
𝑆20 = 1060

9. Therefore, the sum of the first 20 terms of
the arithmetic sequence 15, 19, 23, 27, … is
1060.

10. Solution 2:
Substituting 𝑎1 = 15, 𝑑 = 4 and 𝑛 = 20 in the formula
𝑆 𝑛 =
𝑛
2
[2𝑎1 + (𝑛 − 1)𝑑], we have
𝑆20 =
20
2
[2(15) + (20 − 1)4]
𝑆20 =
20
2
[2(15) + (19)4]
𝑆20 =
20
2
[2(15) + 76]
𝑆20 =
20
2
(30 + 76)
𝑆20 =
20
2
106
𝑆20 = 10(106)
𝑺 𝟐𝟎 = 𝟏𝟎𝟔𝟎

11. Using an alternative solution, the
sum of the first 20 terms of the
arithmetic sequence
15, 19, 23, 27, … is still 1060.

12. Illustrative Example 2:
How many terms is needed for – 3, 2, 7, …
to have a sum of116?
Solution:
Using the formula for the sum of
arithmetic sequence𝑆 𝑛 = 𝑛2 [2𝑎1 +
(𝑛 − 1)𝑑], substitute𝑆 𝑛 = 116, 𝑎1 =
– 3 𝑎𝑛𝑑 𝑑 = 5. We have

13. 116 =
𝑛
2
[2(−3) + (𝑛 − 1)5]
116 =
𝑛
2
[2(−3) + 5𝑛 − 5]
116 =
𝑛
2
[−6 + 5𝑛 − 5]
116 =
𝑛
2
[5𝑛 − 11]
2 [116 =
𝑛
2
(5𝑛 − 11)]
232 = 𝑛(5𝑛 − 11)
232 = 5𝑛2 − 11𝑛
5𝑛2 − 11𝑛 − 232 = 0

14. Using quadratic formula, we have, 𝑎 = 5; 𝑏 =
– 11; 𝑐 = – 232
𝑛 =
−𝑏± 𝑏2−4𝑎𝑐
2𝑎
𝑛 =
−(−11)± (−11)2−4(5)(−232)
2(5)
𝑛 =
11± 121+4640
10
𝑛 =
11± 4761
10
𝑛 =
11±69
10
Since we are looking for
the number of terms n,
the only accepted solution
is the positive solution.
That is 𝑛 = 8
Therefore, eight (8) terms
of the sequence –3, 2, 7, …
is needed to have a sum of
116.

15. Illustrative Example 3: Find the sum of the first 40 terms
of the arithmetic sequence whose first and third terms
are 15 and 21, respectively.
Solution:
We need to solve first for d by substituting 𝑎1 =
15, 𝑎3 = 21 and 𝑛 = 3 to the formula
𝑎 𝑛 = 𝑎1 + (𝑛 − 1)𝑑
21 = 15 + (3 − 1)𝑑
21 = 15 + 2𝑑
6 = 2𝑑
𝑑 = 3

16. Solving for 𝑆40, substitute 𝑎1 = 15, 𝑛 =
40 𝑎𝑛𝑑 𝑑 = 3 to the formula
𝑆 𝑛 =
𝑛
2
[2𝑎1 + (𝑛 − 1)𝑑]
𝑆40 =
40
2
[2(15) + (40 − 1)3]
𝑆40 = 20[30 + 117]
𝑺𝟒𝟎 = 𝟐𝟗𝟒𝟎
Therefore, the sum of the first 40 terms is
2940.

17. 1. Is it possible to find the
sum of terms of an
arithmetic sequence?

18. 2. If it is possible to find
its sum, how did you
obtain the sum of the
arithmetic sequence in
the activity?

19. 3. If the sequence contains
large number of terms in the
arithmetic sequence, is it
reasonable to use the previous
solution that you have used?

20. 4. How to get the sum of
terms in an arithmetic
sequence?

21. START TIMERTIME’S UP! TIME LIMIT:
10 minutes
Criteria
Correct Answer  10
Presentation & Creativity
10
Group Cooperation 5
Fastest Group  5

22. a. Find the sum of the first 15 terms of the arithmetic sequence 9, 12, 15, …
Given: 𝑎1 = ____ ; 𝑑 = ____ ; 𝑛 = ____
Solution:
Solve for 𝑎15
𝑎 𝑛 = 𝑎1 + 𝑛 − 1 𝑑
𝑎 𝑛 = ___ + (___ − 1)___ Substitute a1, n and d
𝑎 𝑛= 9 + (____)3 subtract the terms inside the parenthesis
𝑎 𝑛 = 9 + (____) multiply
𝑎 𝑛 = _____ add
Then solve for 𝑆15.
𝑆 𝑛 =
𝑛
2
(𝑎1 + 𝑎𝑛 )
𝑆15 = ___ 2 (____ + ____) Substitute n, 𝑎1 and 𝑎15
𝑆15 =
15
2
(_____) Add the terms inside the parenthesis
𝑆15 =
____
2
Find the product of the numerator
𝑆
15
= ______ Divide

23. b. Find the sum of the first 10 terms of the arithmetic sequence whose 𝑎1 and 𝑎4 are 5 and 38,
respectively.
Given: 𝑎1 = ____ ; 𝑎4 = ____ ; 𝑛 = ____
Solution:
𝑎 𝑛 = 𝑎1 + (𝑛 − 1)𝑑
____ = _____ + (____ − 1) substitute the given
38 = 5 + (____) subtract the terms inside the parenthesis
____ = 3𝑑 apply APE
𝑑 = ____ apply MPE
Solve for 𝑆10.
𝑆 𝑛 =
𝑛
2
[2𝑎1 + (𝑛 − 1)𝑑]
𝑆 𝑛 =
__
2
[2(___) + (____ − 1)____] Substitute a1, n and d
𝑆 𝑛 =
10
2
[____ + (_____)11] Multiply 2 and a1 and then subtract the value of n and 1
𝑆 𝑛 =
10
2
[10 + ____ ] Multiply
𝑆 𝑛 =
10
2
[____ ] Add
𝑆 𝑛 = ____[109] Divide
𝑆 𝑛 = _______ Multiply

29. The sum of terms in an arithmetic
sequence can be solve using the
formula 𝑺 𝒏 =
𝒏
𝟐
(𝒂 𝟏 + 𝒂 𝒏 ) given
the 1st and last term of the
sequence or 𝑺 𝒏 =
𝒏
𝟐
[𝟐𝒂 𝟏 + (𝒏 −
𝟏)𝒅], given the first term and the
common difference.

30. Answer the following problems.
1. Find the seating capacity of a movie
house with 40 𝑟𝑜𝑤𝑠 of seats if there are 15
seats on the first row, 18 𝑠𝑒𝑎𝑡𝑠 in the
second row, 21 𝑠𝑒𝑎𝑡𝑠 in the third row and
so on.

31. 2. A store sells 𝑃ℎ𝑝 1000 worth of Suman sa
Kawit, a delicacy from Kawit, Cavite, during
its first week. The owner of the store has set
a goal of increasing her weekly sales by
𝑃ℎ𝑝 300 each week. If we assume that the
goal is met, find the total sales of the store
during the first 15 𝑤𝑒𝑒𝑘 of operation.

32. 3. Francisco plans to save 𝑃ℎ𝑝 10 every
week on his Bamboo coin bank. If he will
increase his savings by 𝑃ℎ𝑝 1.50 every
succeeding week, how many weeks is
needed to save a total amount of
𝑃ℎ𝑝 219?

34. 1.2940 seats
2.Php. 46, 500.00
3.12weeks

36. Each row of the table contains the values of three
quantities 𝑎1, 𝑑, 𝑎 𝑛, or 𝑆 𝑛 of an arithmetic sequence.
Complete the table below by solving the other two.