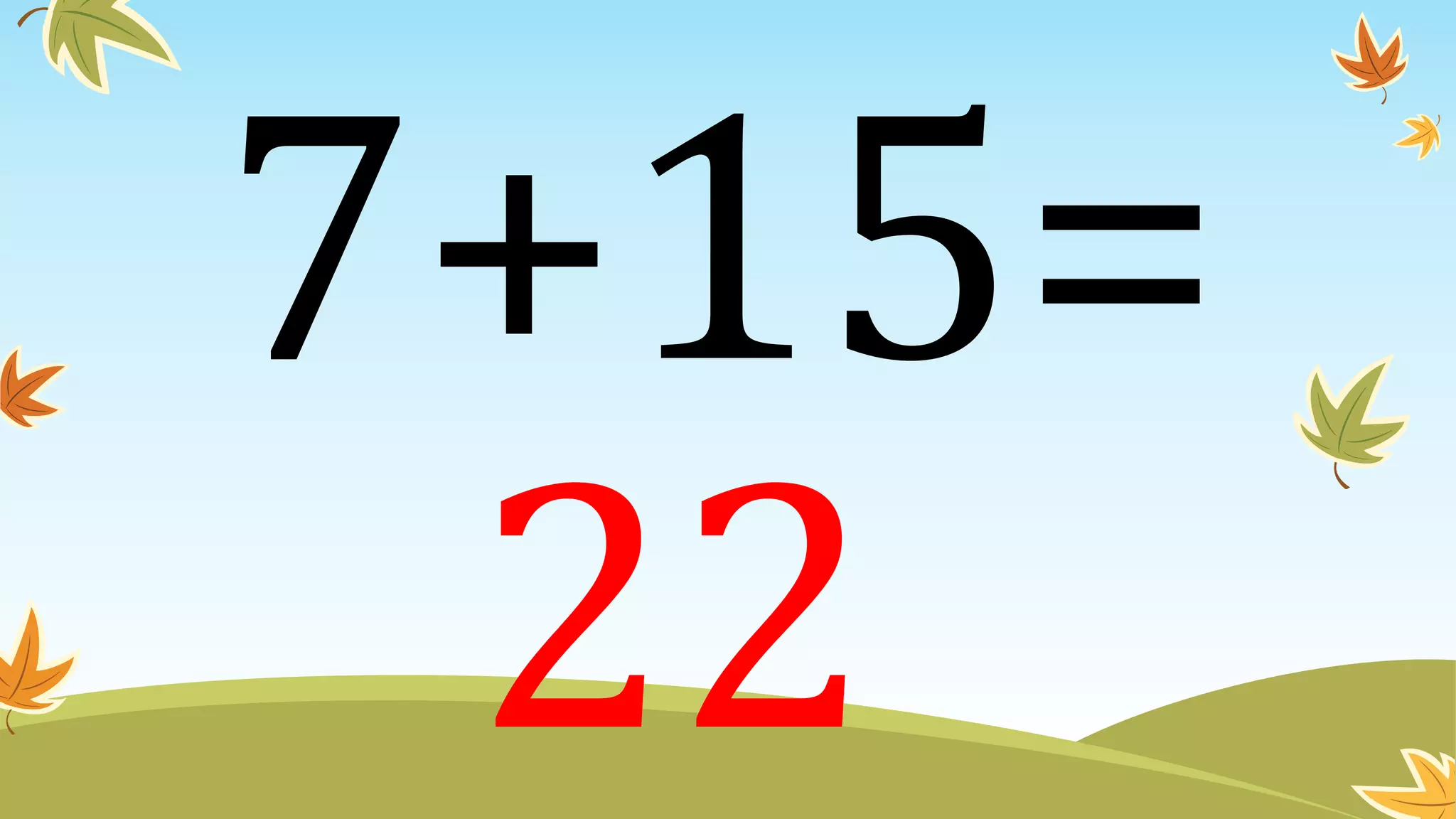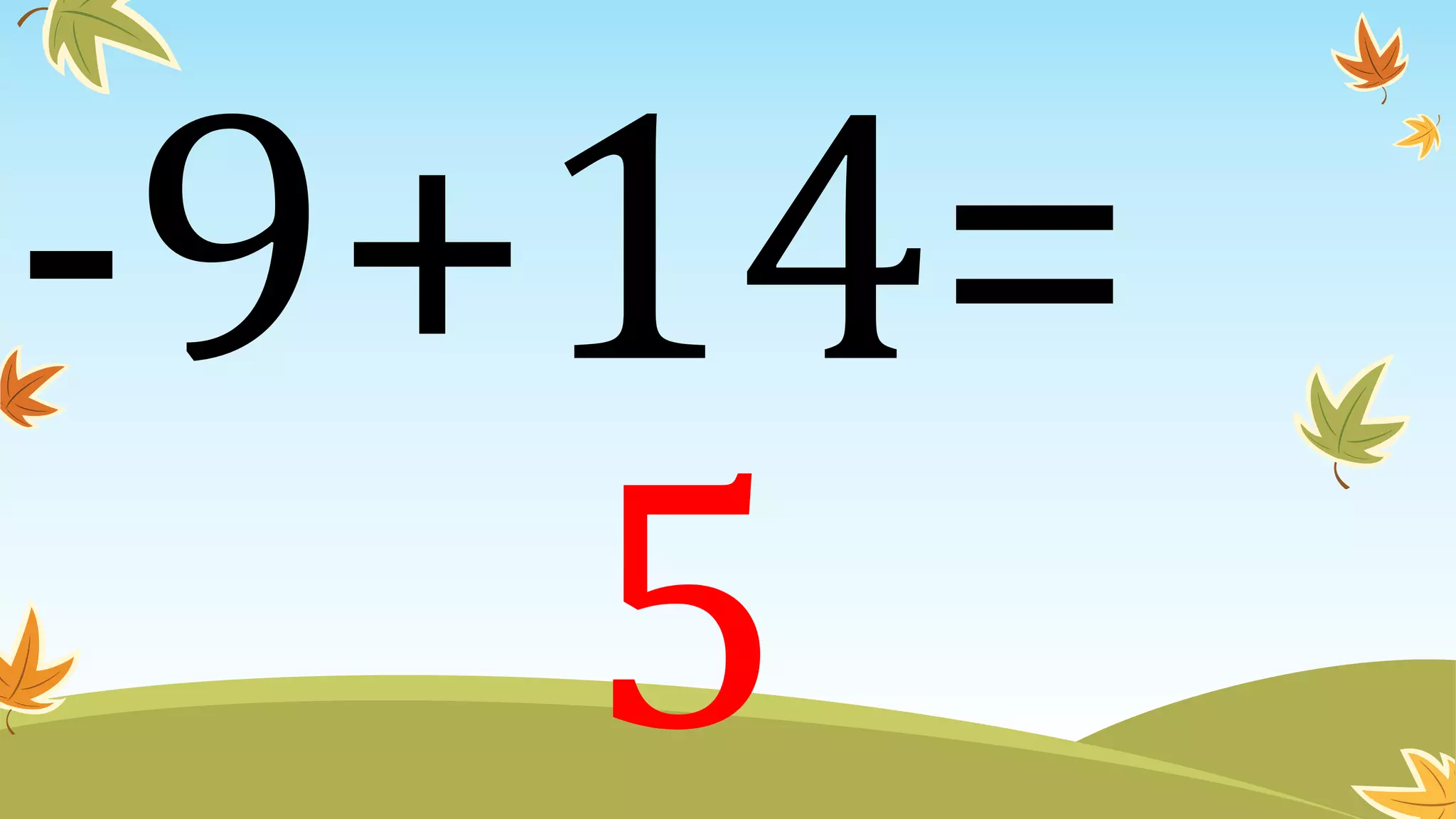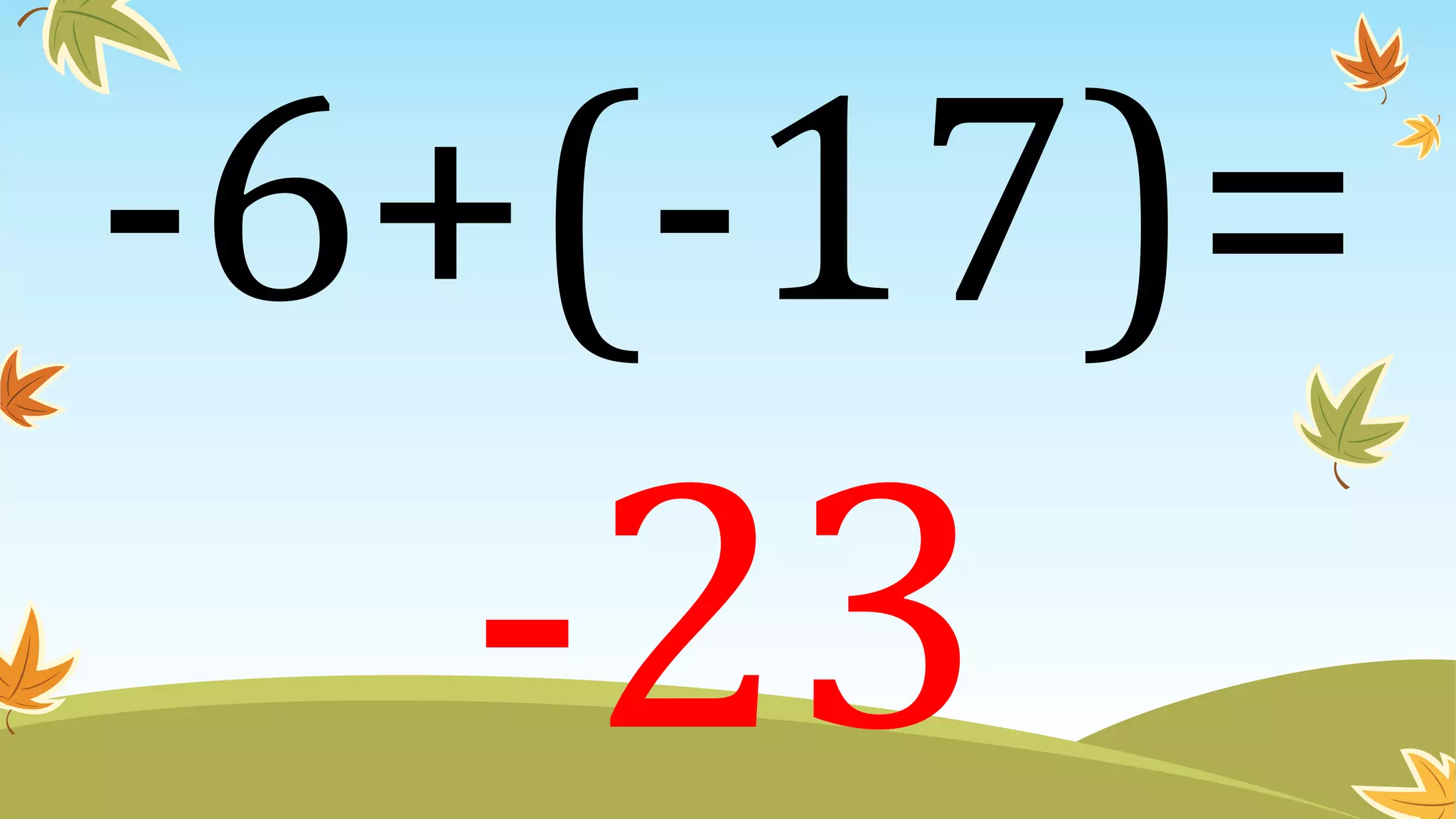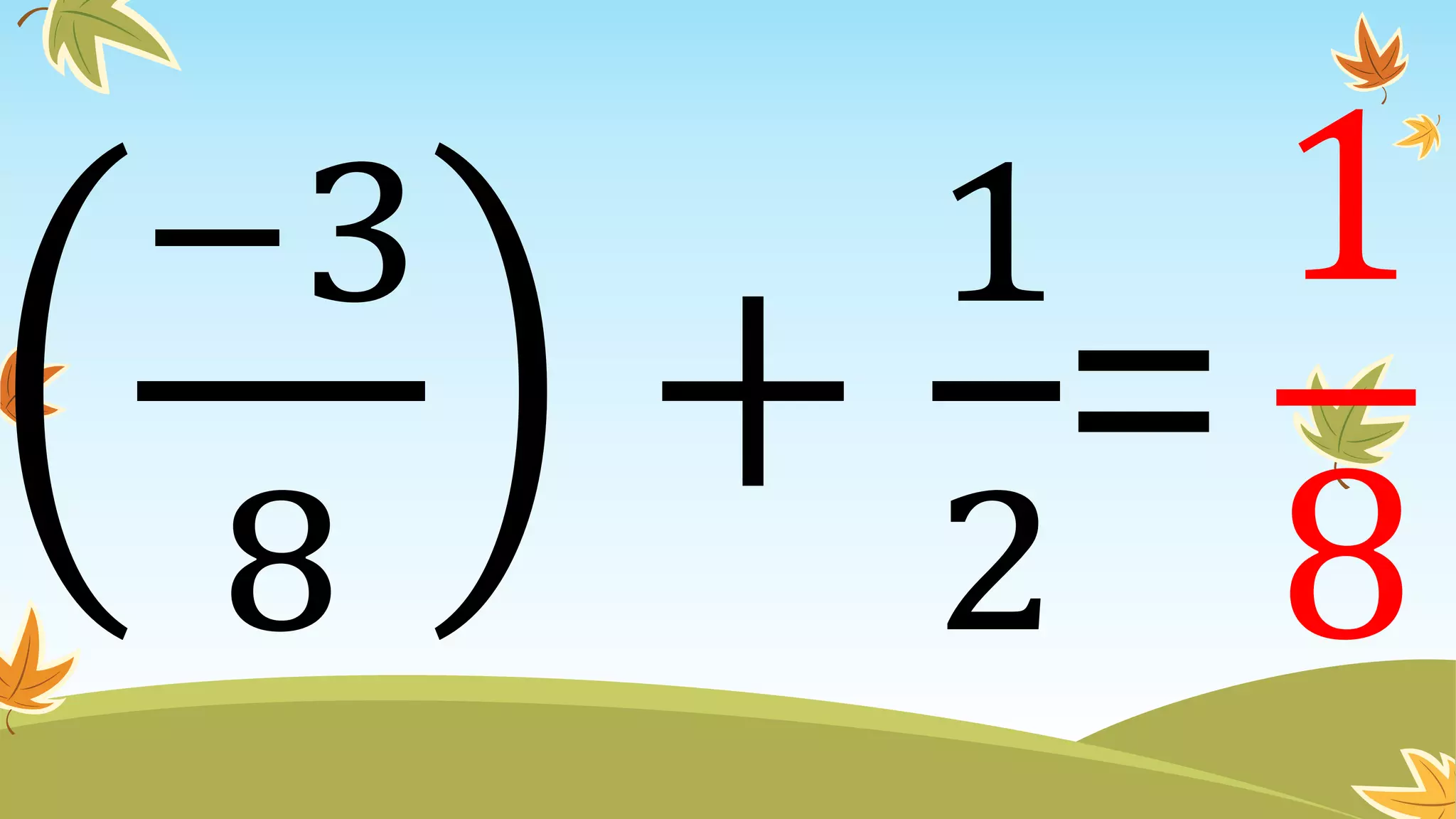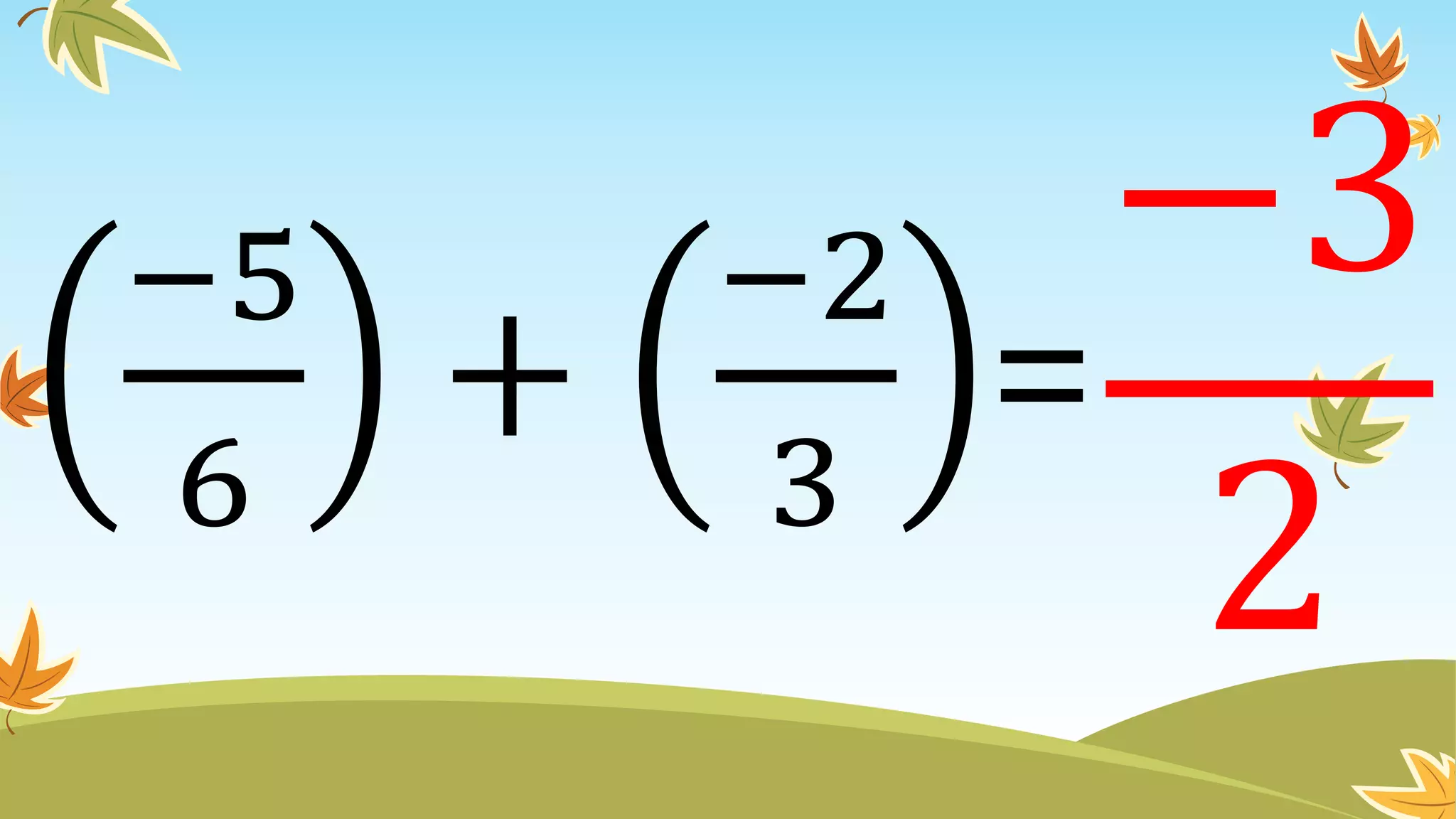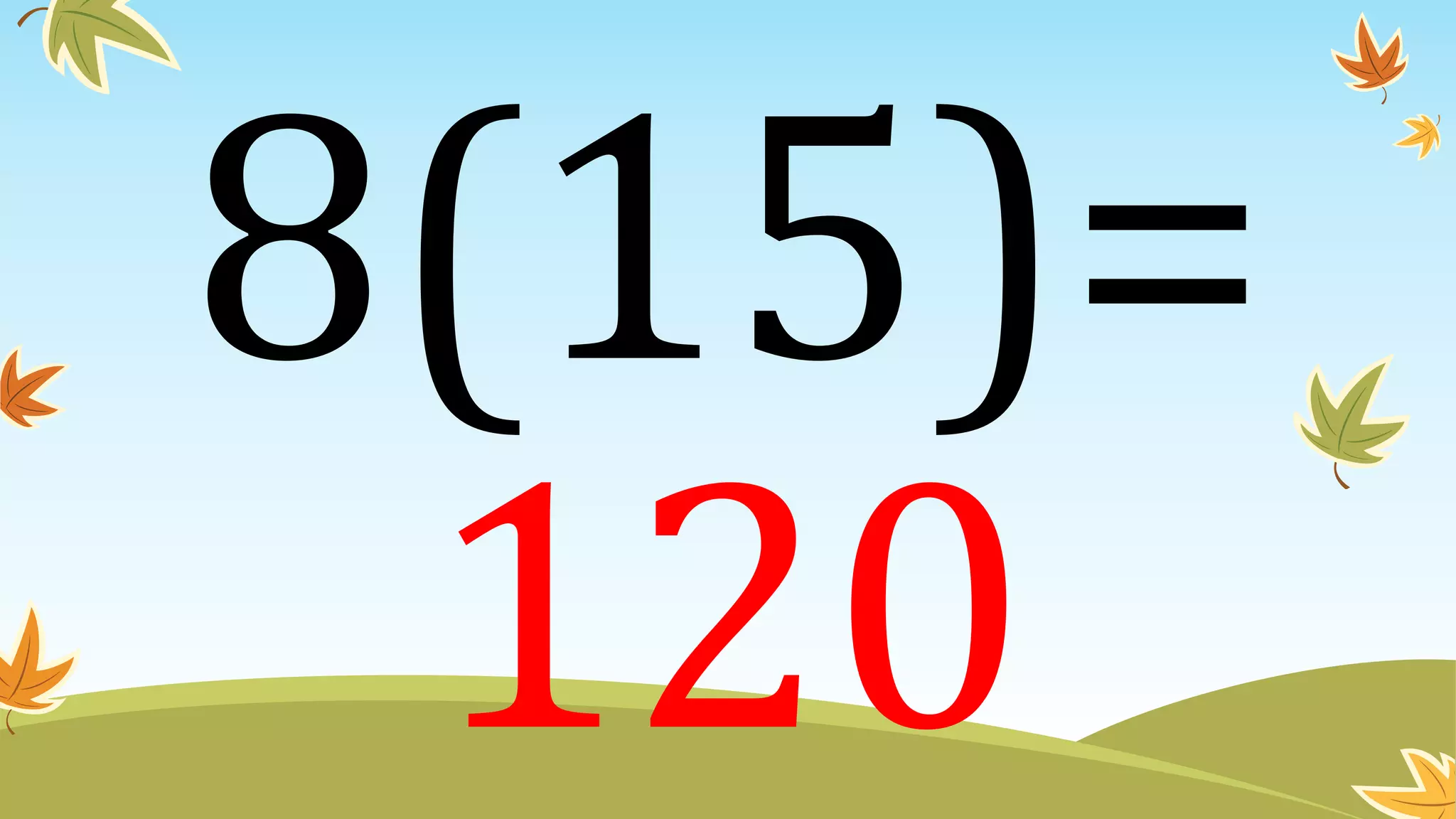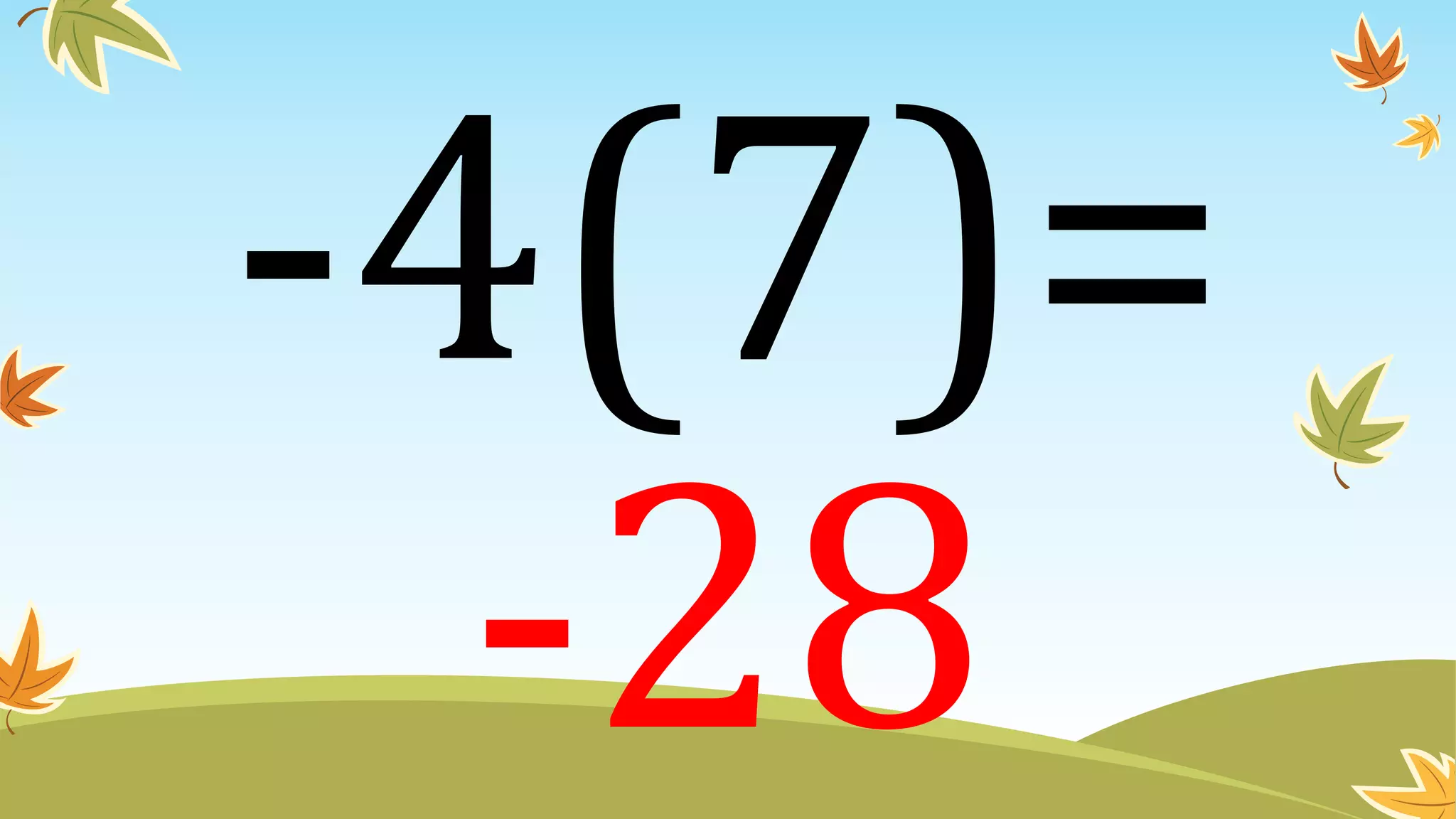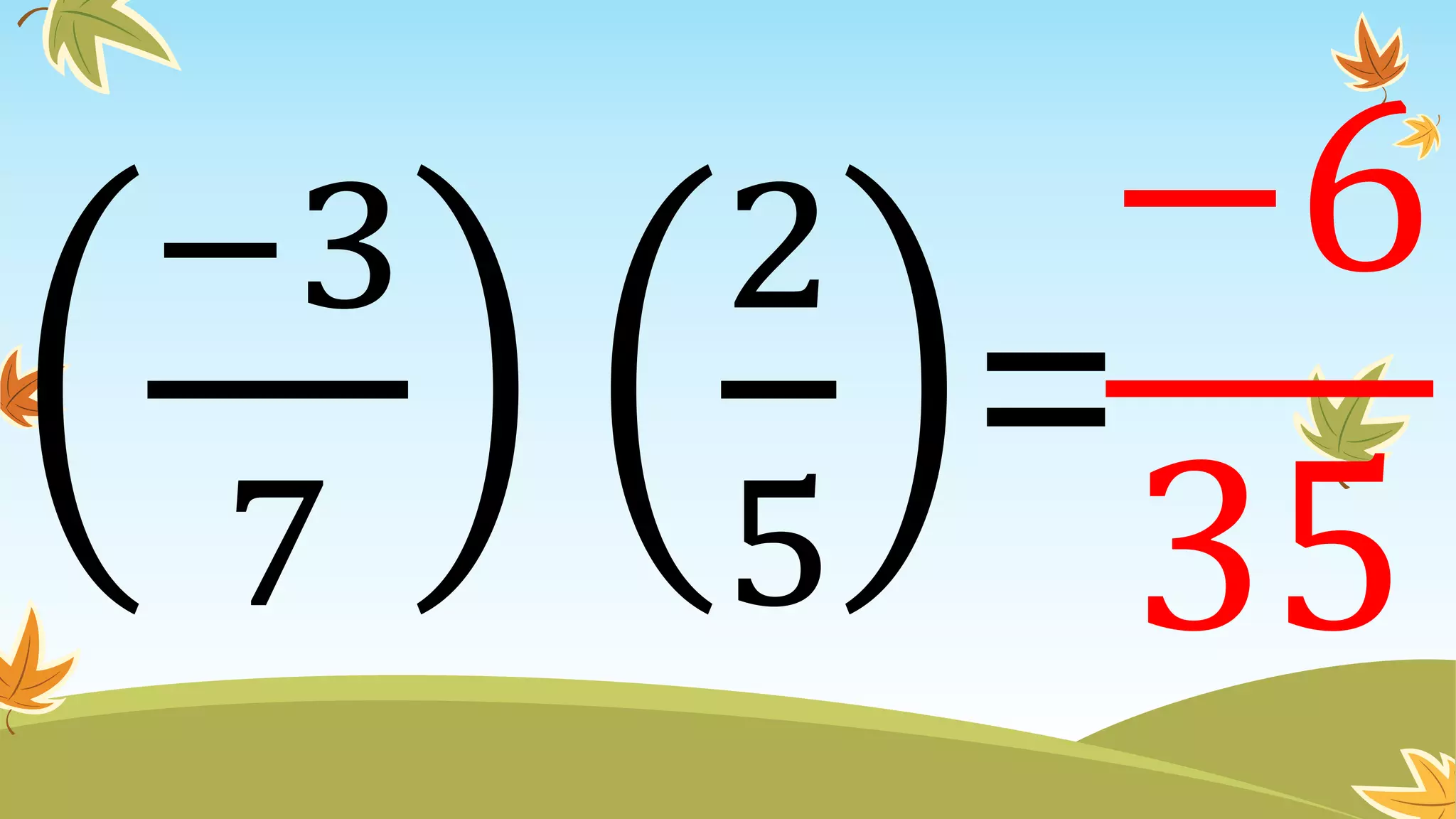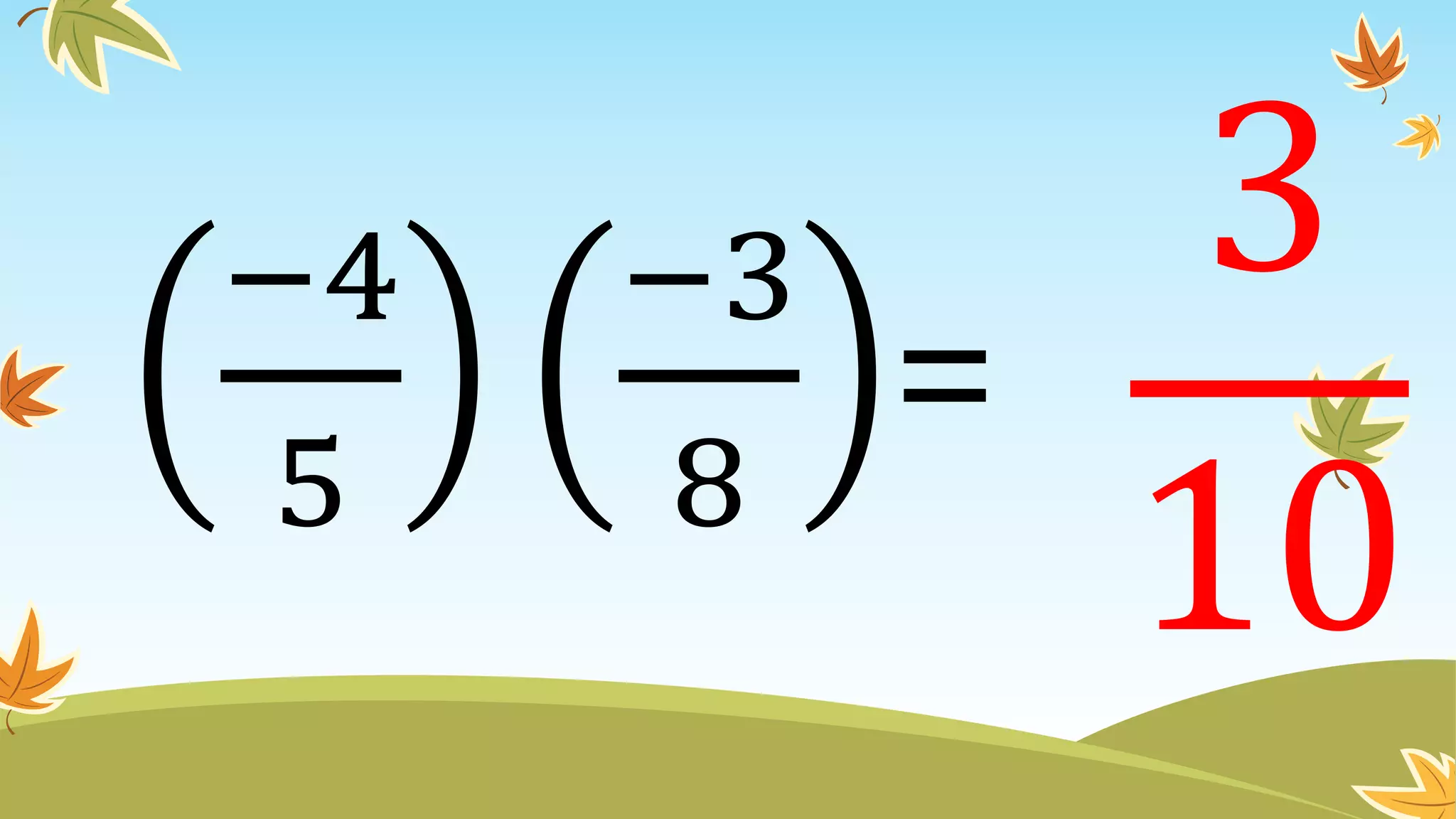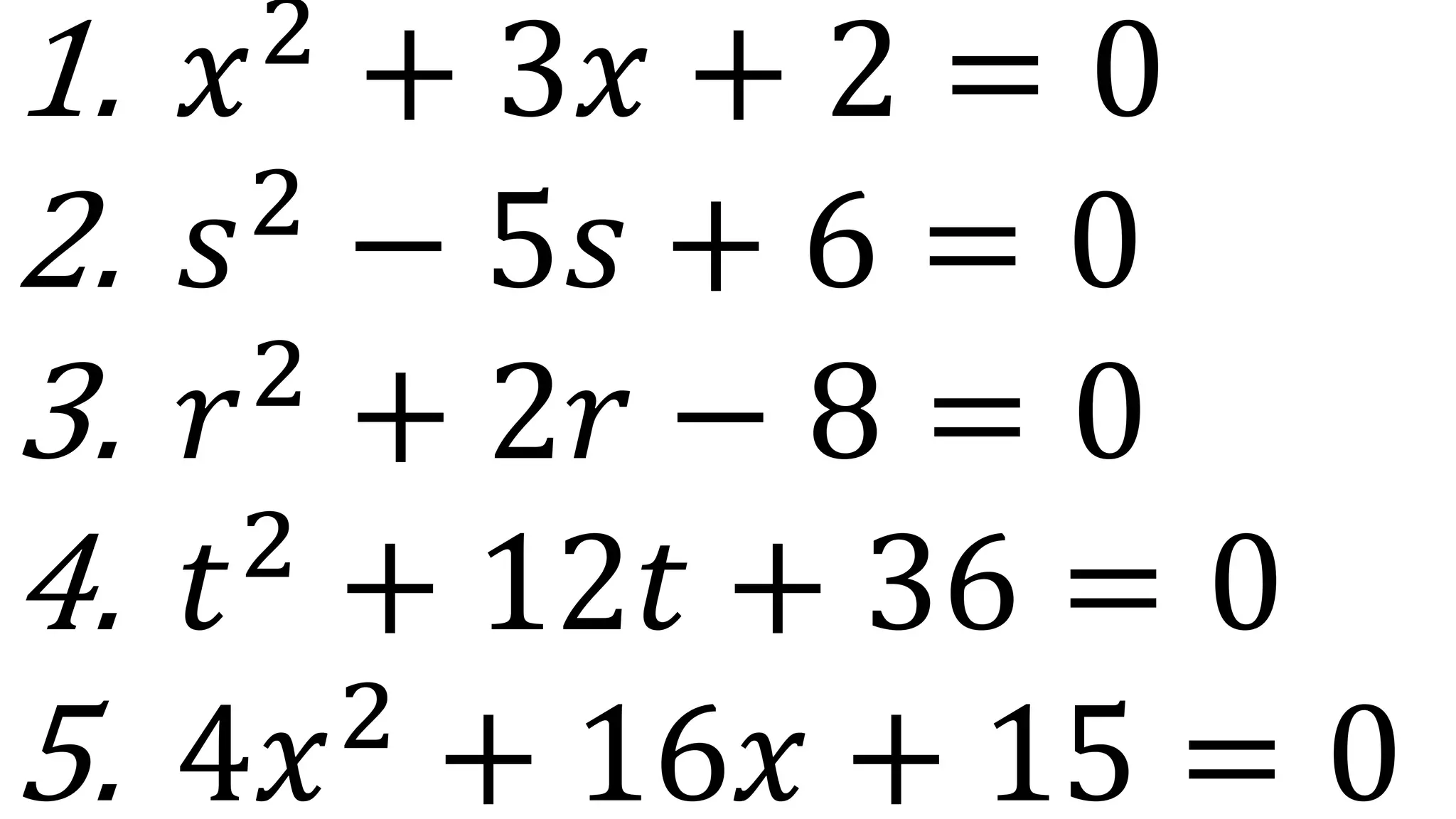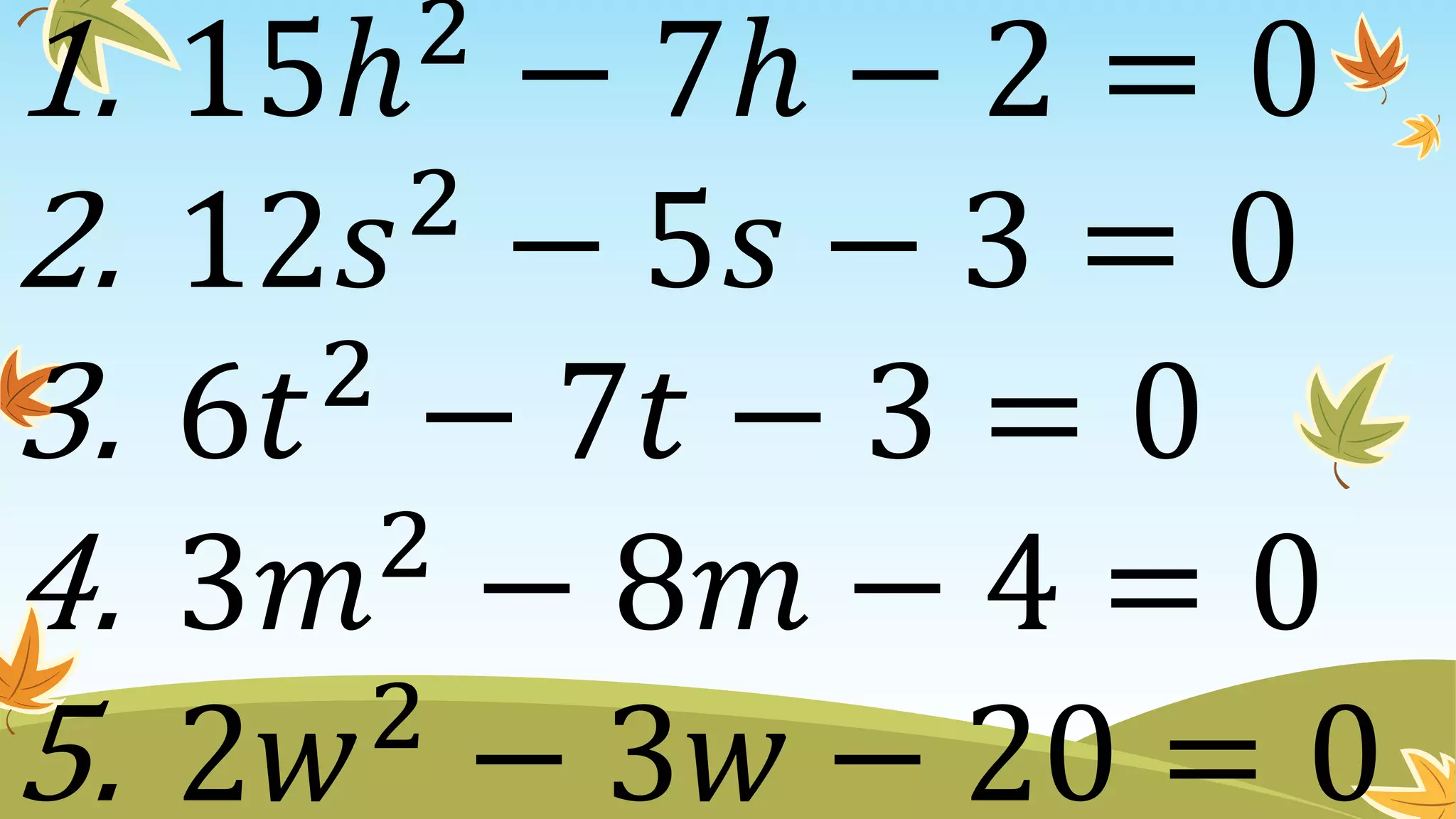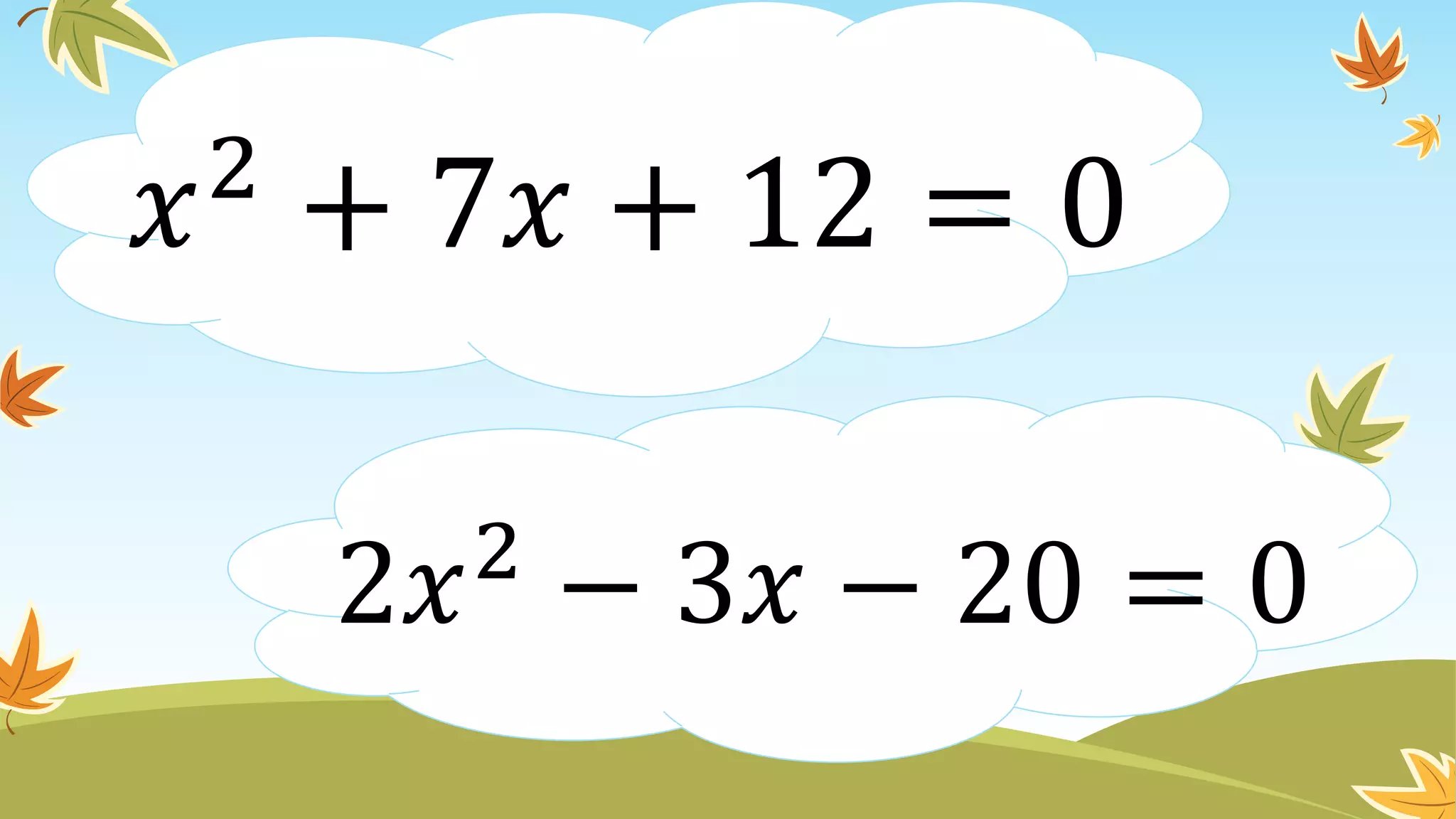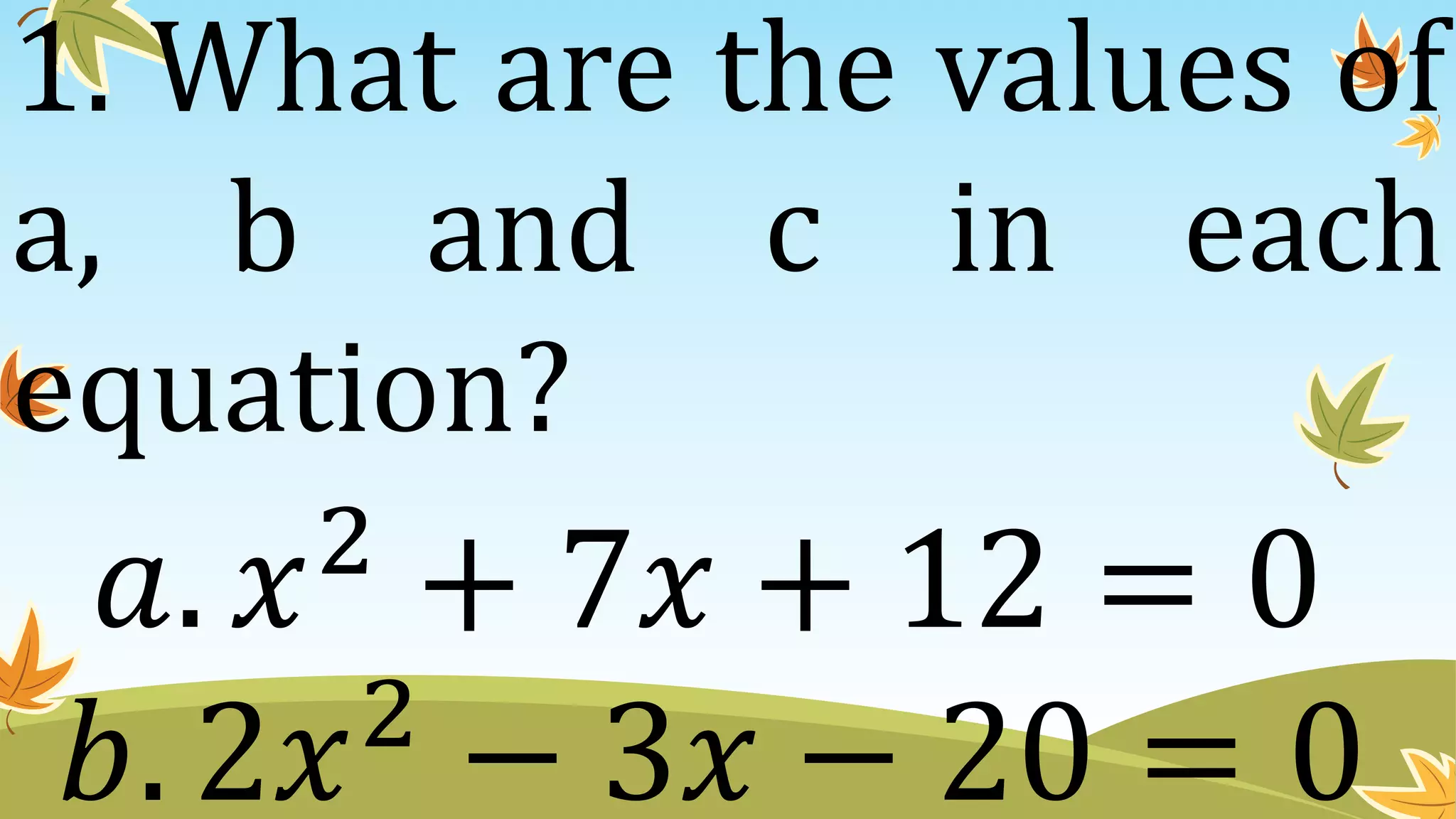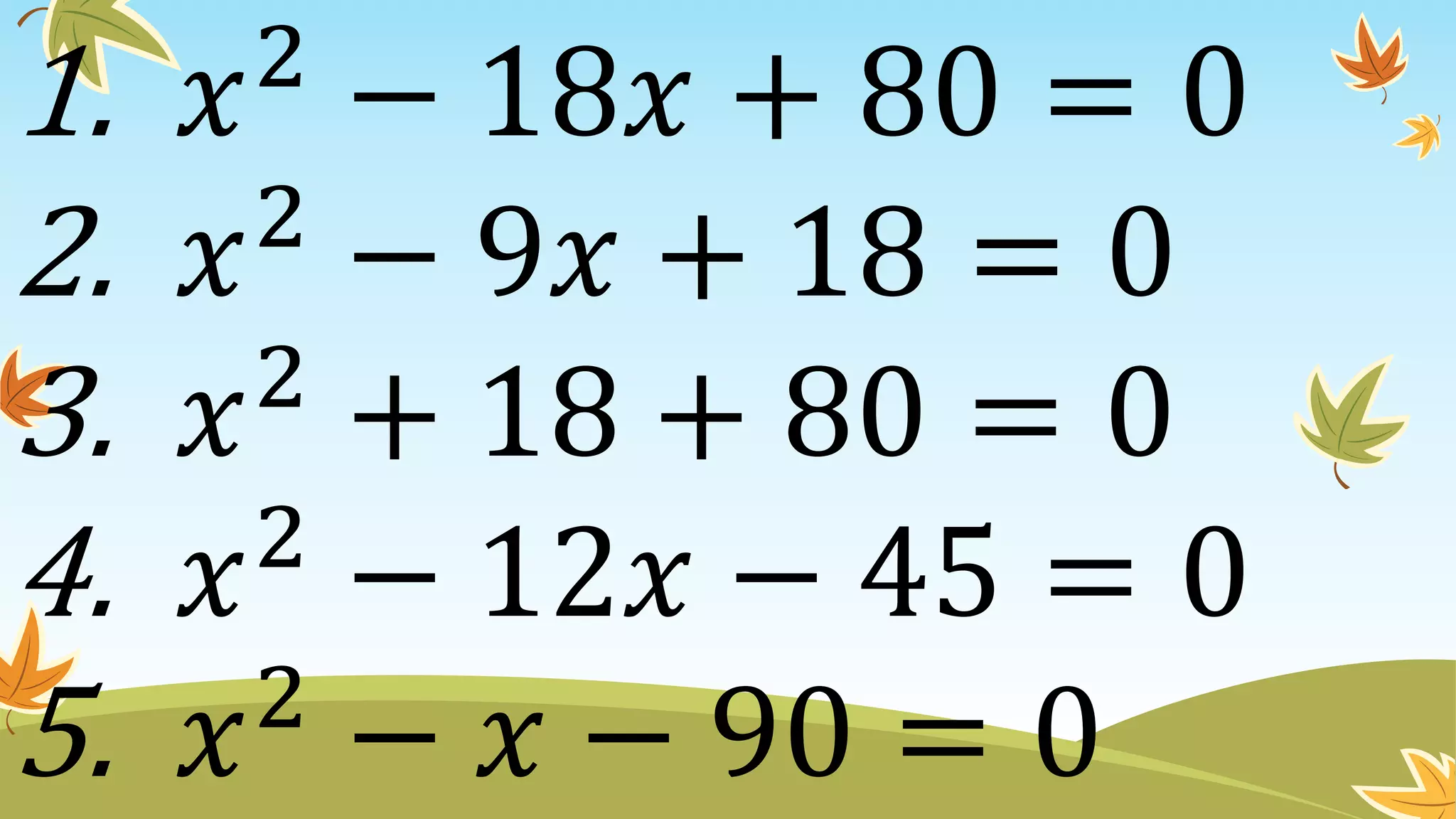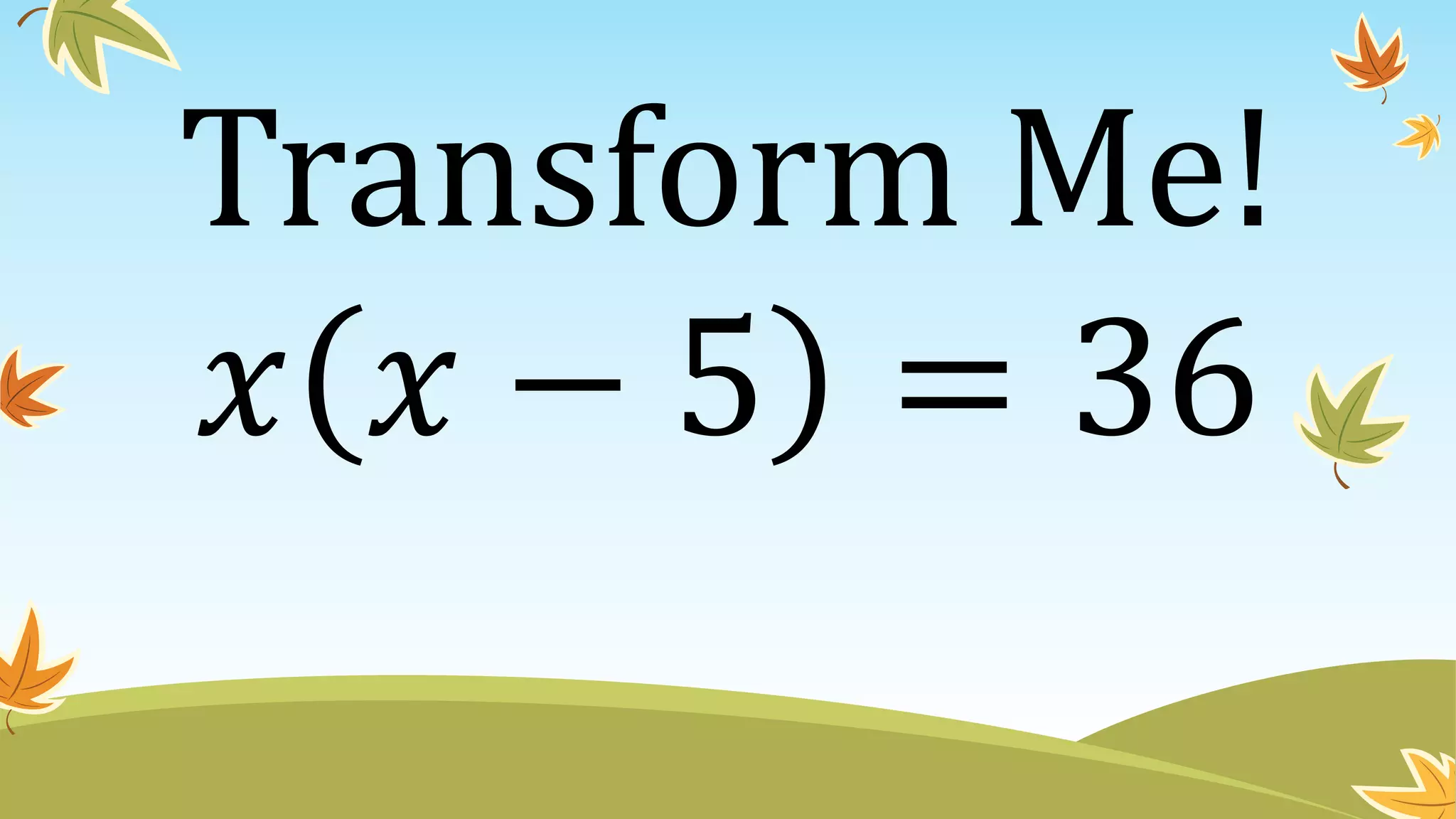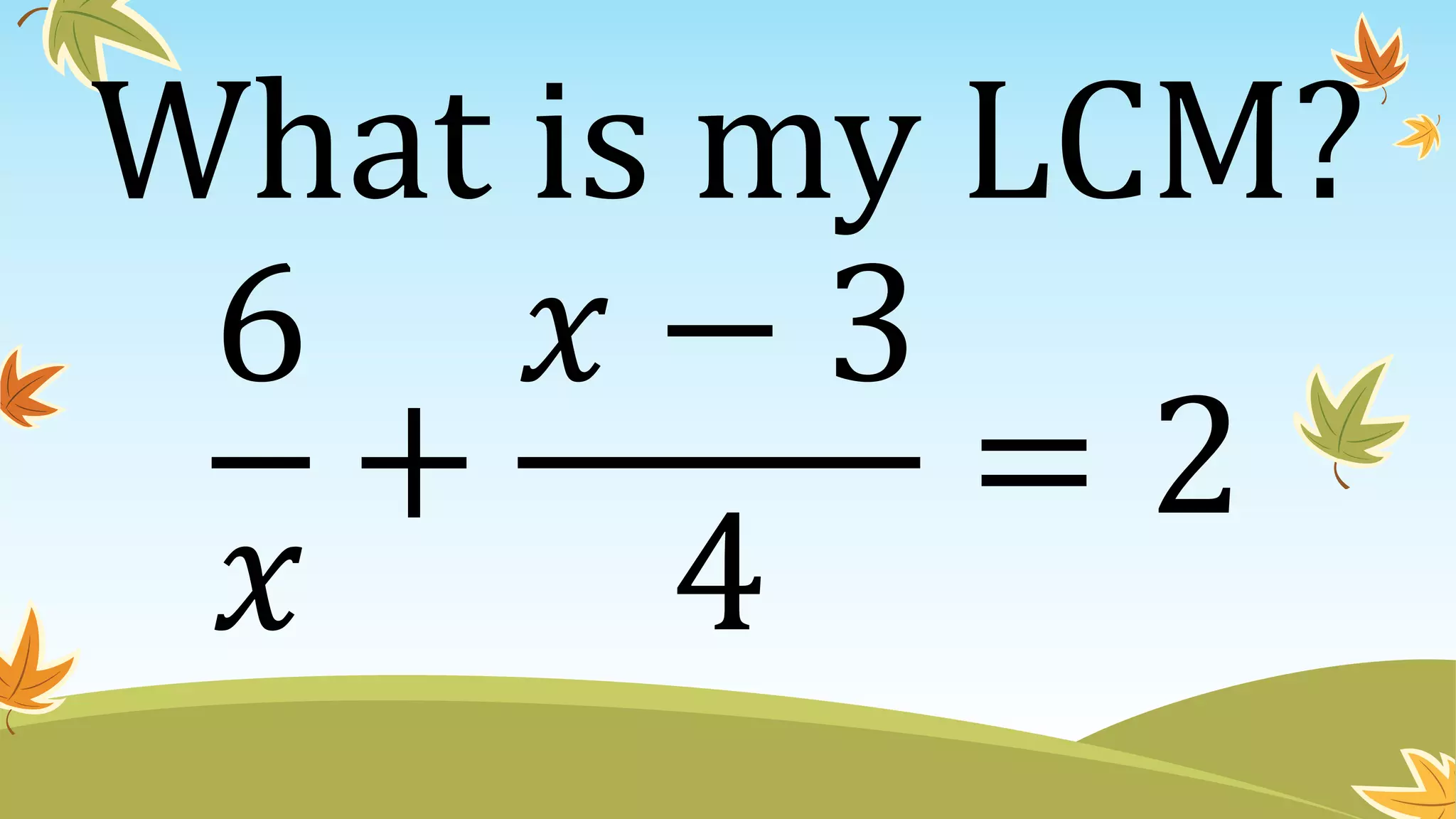This document contains instructions and examples for working with quadratic equations. It includes directions to find the roots of quadratic equations using any method, as well as assignments involving determining values of a, b, and c in quadratic equations; finding the sum and product of roots; and analyzing whether a quadratic equation can be determined from its roots or the sum and product of roots.

1. Let’s Do Addition
and
Multiplication

2. Every correct answer corresponds to
a word to complete

5. -6+(-17)=

6. −3
8
+
1
2
=
1
8

7. −5
6
+
−2
3
=
−3
2

11. −3
7
2
5
=
−6
35

12. −4
5
−3
8
=
3
10

13. The Sum and the
Product of
Quadratic
Equations

14. How did you
determine the
result of each
operation?

15. What mathematics
concepts and
principles did you
apply to arrive at each
result?

16. Compare your answer
with the other groups.
Did you arrive at the
same answer?

17. Exercise # 3
Directions: Find the
roots of the following
quadratic equations
using any method.

18. 1. 𝑥2
+ 3𝑥 + 2 = 0
2. 𝑠2
− 5𝑠 + 6 = 0
3. 𝑟2
+ 2𝑟 − 8 = 0
4. 𝑡2
+ 12𝑡 + 36 = 0
5. 4𝑥2
+ 16𝑥 + 15 = 0

19. Assignment # 3
Directions: Find the
roots of the following
quadratic equations
using any method.

20. 1. 15ℎ2
− 7ℎ − 2 = 0
2. 12𝑠2
− 5𝑠 − 3 = 0
3. 6𝑡2
− 7𝑡 − 3 = 0
4. 3𝑚2
− 8𝑚 − 4 = 0
5. 2𝑤2
− 3𝑤 − 20 = 0

22. Work by My Group
Directions: Use the
quadratic equations
below to answer the
questions that follow.

23. 2𝑥2
− 3𝑥 − 20 = 0
𝑥2
+ 7𝑥 + 12 = 0

24. 1. What are the values of
a, b and c in each
equation?
𝑏. 2𝑥2
− 3𝑥 − 20 = 0
𝑎. 𝑥2
+ 7𝑥 + 12 = 0

25. 2. Determine the roots of each
quadratic equation using any
method.
𝑏. 2𝑥2 − 3𝑥 − 20 = 0
𝑎. 𝑥2
+ 7𝑥 + 12 = 0
𝑥1 = _____, 𝑥2=_____
𝑥1 = _____, 𝑥2=_____

26. 3. Complete the Following table:
Quadratic Equation Sum of
Roots
Product
of Roots
𝑥2
+ 7𝑥 + 12 = 0
2𝑥2
− 3𝑥 − 20 = 0

27. 4. What do you observe
about the sum and the
product of the roots of
quadratic equation in
relation to the values of a, b
and c

28. The sum of the roots of
quadratic equation is
equal to
−𝑏
𝑎
and the
product is equal to
𝑐
𝑎

29. Assignment #4
Directions: Analyze
and answer the
following questions.
Do what is ask.

30. 1. Do you think a
quadratic equation can
be determined given
its roots or solution?
Justify your answer

31. 2. Do you think a
quadratic equation can be
determined given the sum
and product of its roots?
Justify your answer

34. 1. 𝑥2
− 18𝑥 + 80 = 0
2. 𝑥2
− 9𝑥 + 18 = 0
3. 𝑥2
+ 18 + 80 = 0
4. 𝑥2
− 12𝑥 − 45 = 0
5. 𝑥2
− 𝑥 − 90 = 0

35. Proudly Present
Your Group!

36. Equations
Transformable into
Quadratic Equations

37. Transform Me!
𝑥 𝑥 − 5 = 36

38. What is my LCM?
6
𝑥
+
𝑥 − 3
4
= 2

39. 1. How did you
write the
quadratic
equation?

40. 2. What is the
standard form of
quadratic
equations?

41. 3.How did you find the
sum and the difference
of rational algebraic
expressions?

42. 4. How did you
simplify the
resulting
expressions?