![The Big Picture
2 [Williams et al., 2017]
Stochastic Optimal Control Theory
• “Optimality” defined by Bellman’s
principle of optimality.
• Solution methods based on stochastic
dynamic programming.
Information Theoretic Control Theory
• “Optimality” defined in the sense of
Legendre transform.
• Solution methods based on forward
sampling of stochastic differential
equations.
Two fundamentally different approaches to stochastic control problems.](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
Recommended
More Related Content
What's hot
What's hot (20)
Similar to Stochastic Optimal Control & Information Theoretic Dualities
Similar to Stochastic Optimal Control & Information Theoretic Dualities (20)
Recently uploaded
Recently uploaded (20)
Stochastic Optimal Control & Information Theoretic Dualities
- 1. Stochastic Optimal Control & Information Theoretic Dualities MSL Group Meeting, November 10th, 2017 Haruki Nishimura PART 1: INTRODUCTION TO STOCHASTIC CONTROL
- 2. The Big Picture 2 [Williams et al., 2017] Stochastic Optimal Control Theory • “Optimality” defined by Bellman’s principle of optimality. • Solution methods based on stochastic dynamic programming. Information Theoretic Control Theory • “Optimality” defined in the sense of Legendre transform. • Solution methods based on forward sampling of stochastic differential equations. Two fundamentally different approaches to stochastic control problems.
- 3. The Big Picture 3 [Williams et al., 2017] V(x0) Values of terminal states x 0 Stochastic Dynamic Programming Forward Sampling of SDEs Space of value function State space
- 4. Outline Part 1 (Today) Stochastic Optimal Control › Deterministic optimal control, Bellman’s principle of optimality › Wiener processes and stochastic differential equations › Stochastic Hamilton-Jacobi-Bellman equation Information Theoretic Control › Legendre transformation Part 2 (Tentative, 12/1) › Helmholtz free energy and its interpretations › Relations to Bellman’s principle of optimality & linearly solvable optimal control problems › Algorithms and applications › Limitations
- 5. Deterministic Optimal Control Problem Consider a continuous-time optimization problem of the following form: where 5 Terminal Cost Per-stage Cost : control input profile
- 6. How to solve for the optimal control? 1. Pontryagin’s Maximum Principle • Based on calculus of variations. • Solve a system of ODEs (2n). (Hamiltonian System) • Open-loop Specification. 6 2. Bellman’s Principle of Optimality • Based on dynamic programming. • Solve an n-dimensional PDE. (HJB Equation) • Closed-loop Specification.
- 7. Hamilton-Jacobi-Bellman Equation “Optimal cost-to-go” or “value function” Let’s find a recursive structure in V via Dynamic Programming. 7 t0 tft’ If the blue is optimal, then the red is necessarily optimal as well.
- 8. Hamilton-Jacobi-Bellman Equation Taylor expand V(t+dt, x(t+dt)) around V(t,x(t)). Substitute this into the original equation with dx = f(t,x,u)dt. Rearrange terms and take the limit dt -> 0. 8
- 9. Hamilton-Jacobi-Bellman Equation Boundary Condition: Numerically solve backwards in time for all (t,x) to obtain the closed- loop optimal control policy: 9
- 10. Stochastic Optimal Control Problem Goal is to derive HJB. Any differences from the deterministic case? 10 1. The dynamics is governed by a stochastic differential equation. 2. Uncertainties about future state trajectories.
- 11. Example: The Drunken Spider Problem Presence of noise (alcohol) can change the optimal behavior significantly. 11 • Without noise, the spider will cross the bridge. • When drunk, the cost of crossing the bridge increases and the spider should go around the lake. [Kappen, 2005]
- 12. What is the stochasticity in the dynamics? Recall that the dynamics is described by the following stochastic differential equation. where wt is a stochastic process called the Wiener Process (a.k.a. Standard Brownian Motion). 12
- 13. The Wiener Process A type of Gaussian Process with “good” properties to model random behavior that evolves over time. 13 Applications: • Finance • Physics • Chemistry • Stochastic Control Theory …and more. Image URL: https://github.com/matthewfieger/wiener_process
- 14. The Wiener Process 1. Continuity: wt is continuous in t with probability 1. 2. Gaussianity:wt+s – ws is distributed according to N(0,t). 3. Independnce: wt+s – ws is independent of {wr}r<=s. 4. Stationarity:The distribution for wt+s – ws is independent of s. 14
- 15. The Wiener Process 1. Continuity: wt is continuous in t with probability 1. 2. Gaussianity:wt+s – ws is distributed according to N(0,t). 3. Independnce: wt+s – ws is independent of {wr}r<=s. 4. Stationarity:The distribution for wt+s – ws is independent of s. 15
- 16. The Wiener Process 1. Continuity: wt is continuous in t with probability 1. 2. Gaussianity:wt+s – ws is distributed according to N(0,t). 3. Independnce: wt+s – ws is independent of {wr}r<=s. 4. Stationarity:The distribution for wt+s – ws is independent of s. 16
- 17. The Wiener Process 1. Continuity: wt is continuous in t with probability 1. 2. Gaussianity:wt+s – ws is distributed according to N(0,t). 3. Independnce: wt+s – ws is independent of {wr}r<=s. 4. Stationarity:The distribution for wt+s – ws is independent of s. 17
- 18. Stochastic Differential Equation Easiest to think of dwt as a Gaussian white noise with . Going back to our original equation, Note that it is not written in (dx/dt) form because the Wiener process is shown to be nowhere- differentiable with probability 1. 18 Drift term Diffusion term
- 19. Proof of Indifferentiability Assume wt is differentiable at some t0. Then the derivative w’ must exist. That is, Without loss of generality take t >= t0. Now the definition of the Wiener process gives and thus, The probability of the quantity |.| exceeding any positive ε is always positive, and can be made arbitrarily large by taking t sufficiently close to t0. Q.E.D. 19
- 20. Deterministic HJB (Recap) “Optimal cost-to-go” or “value function” Let’s find a recursive structure in V via Dynamic Programming. 20 t0 tft’ If the blue is optimal, then the red is necessarily optimal as well.
- 21. Deriving Stochastic HJB Equation Define the value function as before. Establish a recursive formula for V. As usual, our strategy is to Taylor expand V(t+dt,x(t+dt)) and consider only the terms that are O(dt). 21
- 22. Taylor Expansion & Itô‘s Lemma Under the Wiener noise, the chain rule gives Why? 22
- 23. Taylor Expansion & Itô‘s Lemma Under the Wiener noise, the chain rule gives We need to consider the 2nd order term. This result can be generalized and is referred to as Itô‘s lemma. 23
- 24. Stochastic HJB Equation After substitution and taking the limit dt -> 0, we obtain Notice the difference from the deterministic HJB equation: The magnitude of the diffusion term b(x) affects the optimal control through the value function. 24
- 25. Solving HJB Equation In general HJB becomes an n-dimensional PDE (in Vx), which needs to be solved backward in time. • Second-order, nonlinear PDE. • Exponential growth of the computational and storage requirements as the dimension n increases. • Exception: LQG control 25
- 26. Summary – Stochastic Optimal Control Problem Formulation: Solution Method: Stochastic Dynamic Programming Solve HJB or approximate the problem to alleviate the complexity. 26
- 27. Outline Part 1 (Today) Stochastic Optimal Control › Deterministic optimal control, Bellman’s principle of optimality › Wiener processes and stochastic differential equations › Stochastic Hamilton-Jacobi-Bellman equation Information Theoretic Control › Legendre transformation Part 2 (Tentative, 12/1) › Helmholtz free energy and its interpretations › Relations to Bellman’s principle of optimality & linearly solvable optimal control problems › Algorithms and applications › Limitations
- 28. Basic Idea • Instead of solving for the value function, we aim at finding a lower bound on the expected cost that can be easily evaluated. • Use of an information theoretic inequality. Theorem (Legendre Transform, Theodorou 2015) Let and . Consider two probability distributions p and q over x. Then for , the following inequality holds. 28 Note: q is assumed to be absolutely continuous w.r.t. p.
- 29. Proof of the Legendre Transform Change of measure from p to q gives Apply Jensen’s inequality to RHS. Multiply with –λ (< 0) to get the inequality. 29
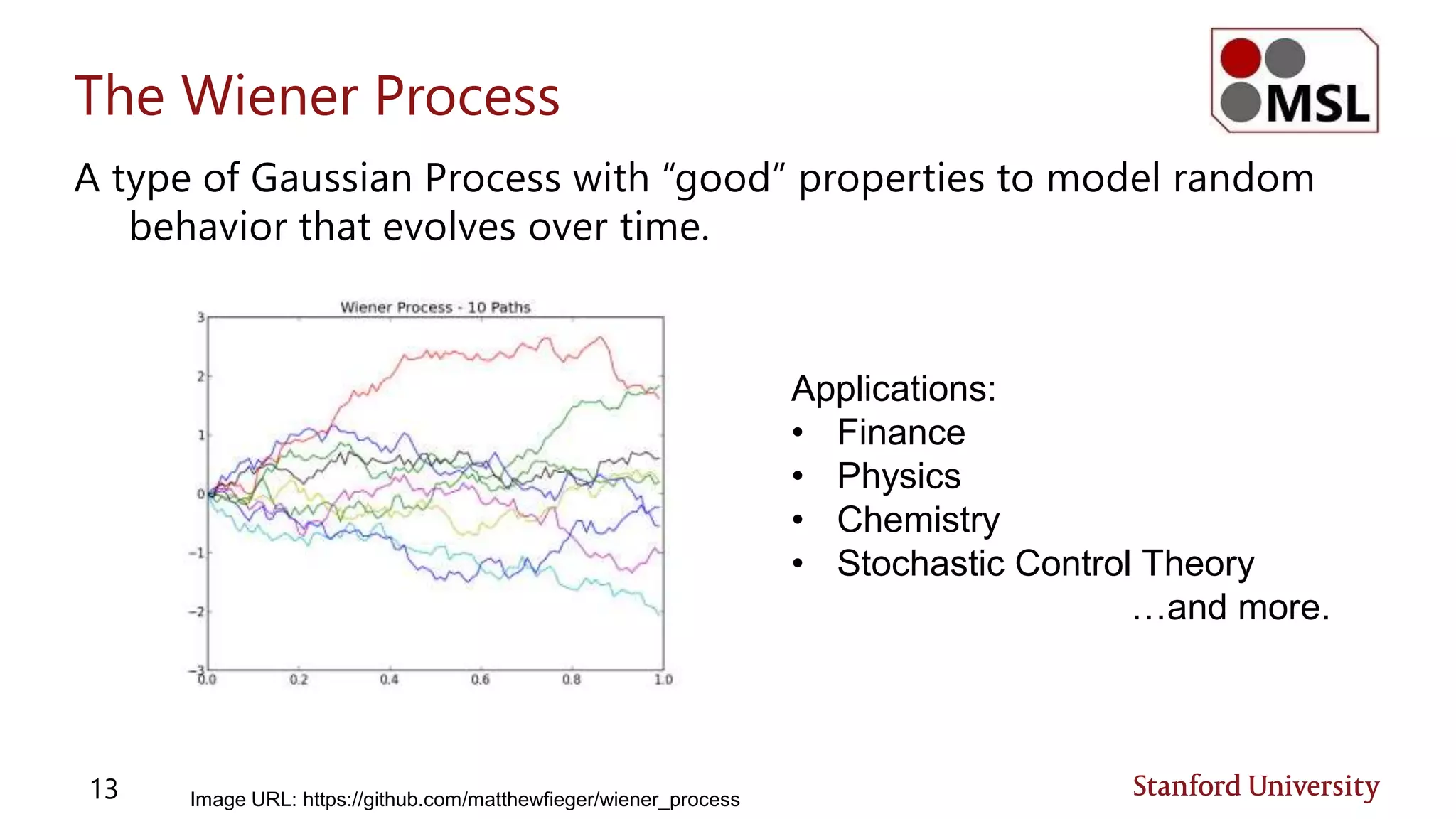
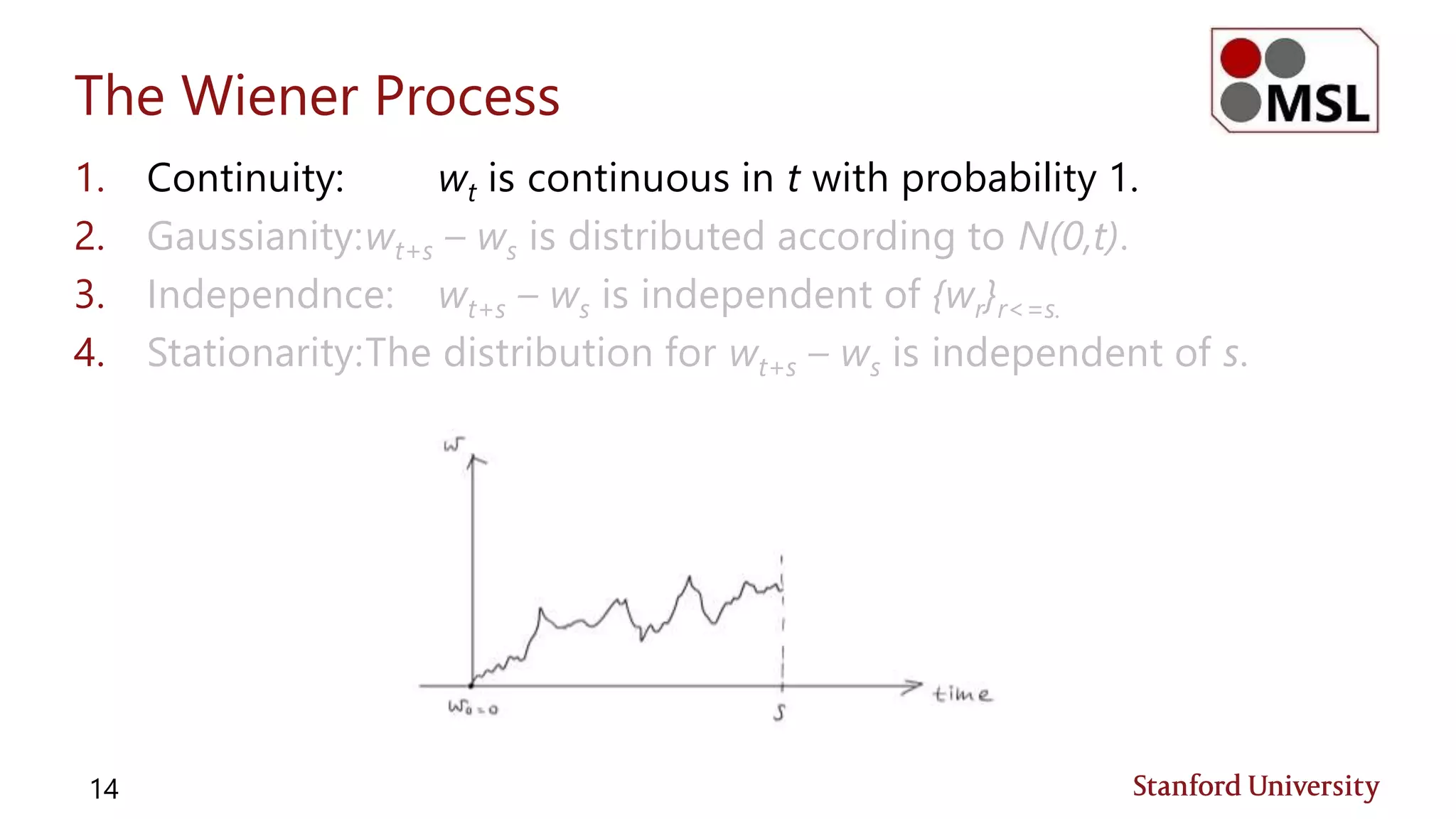
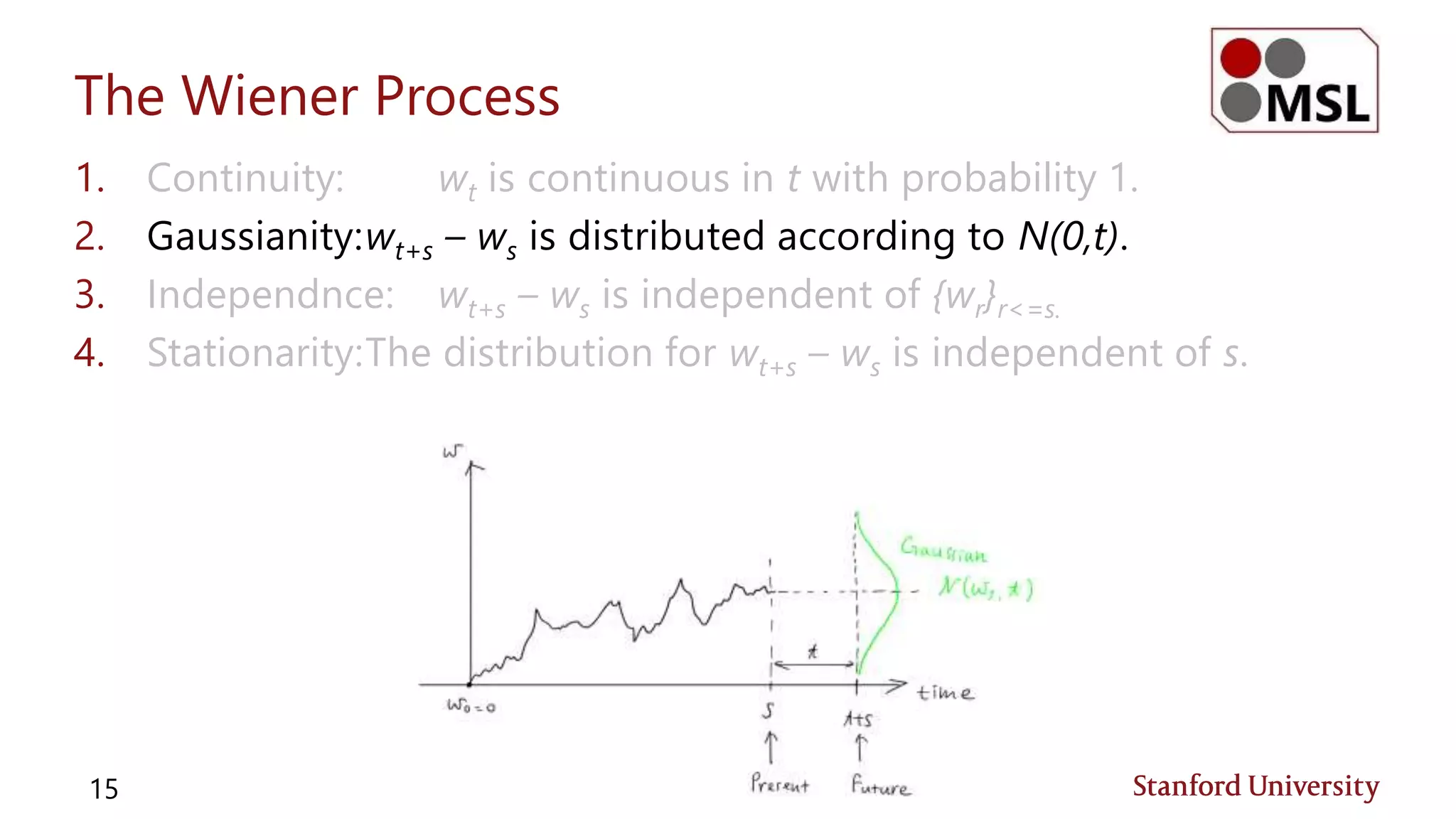
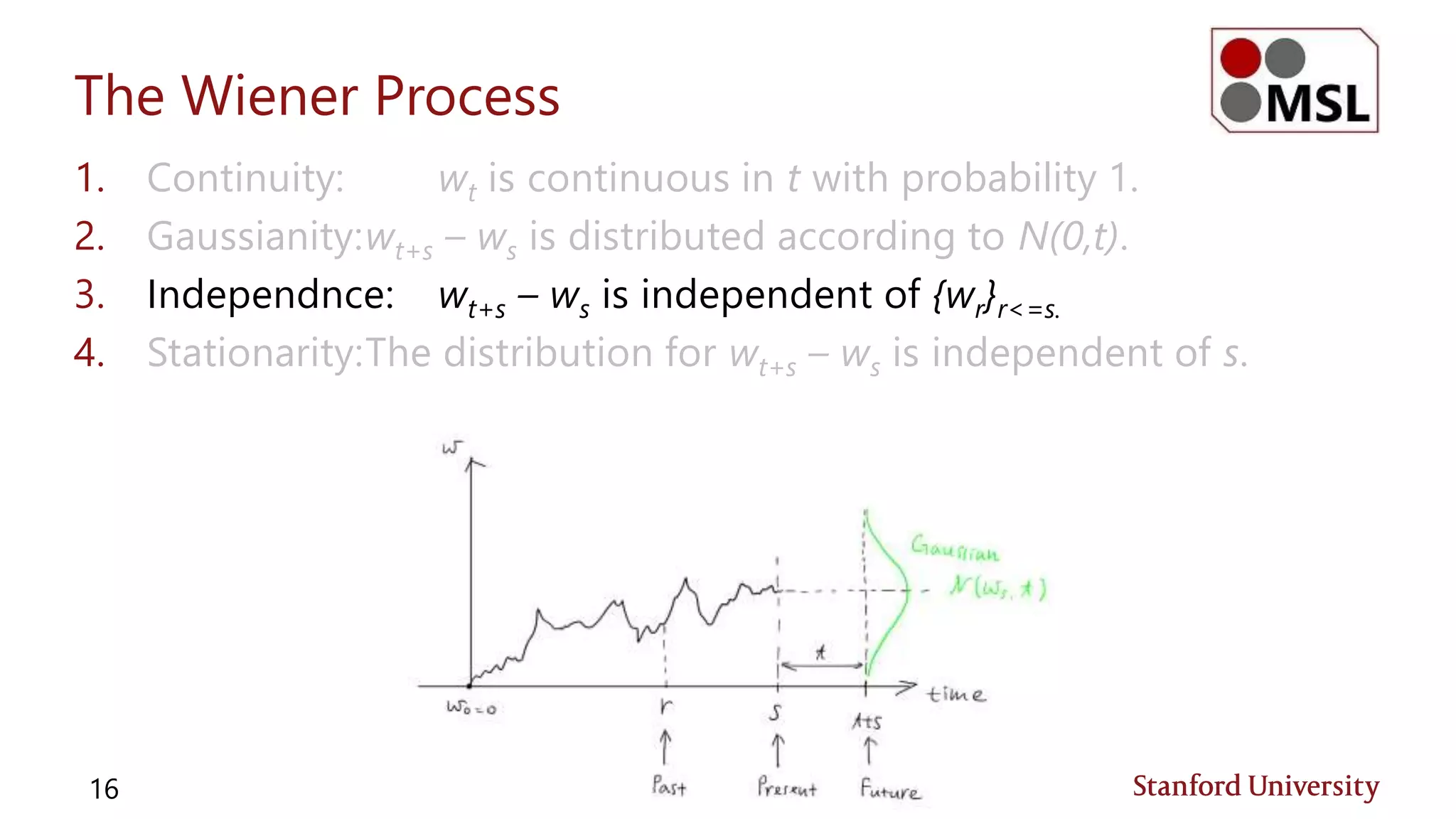
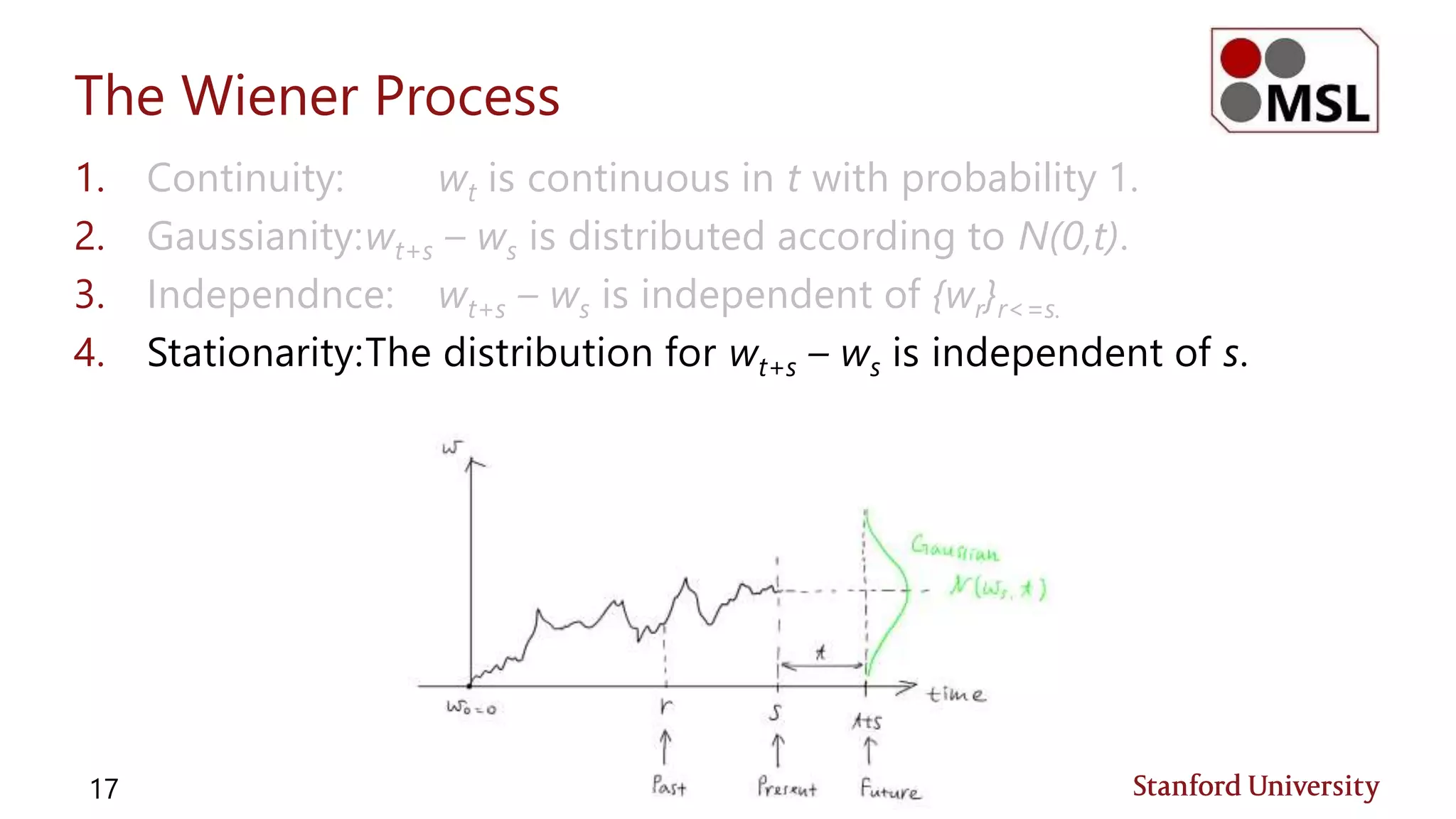
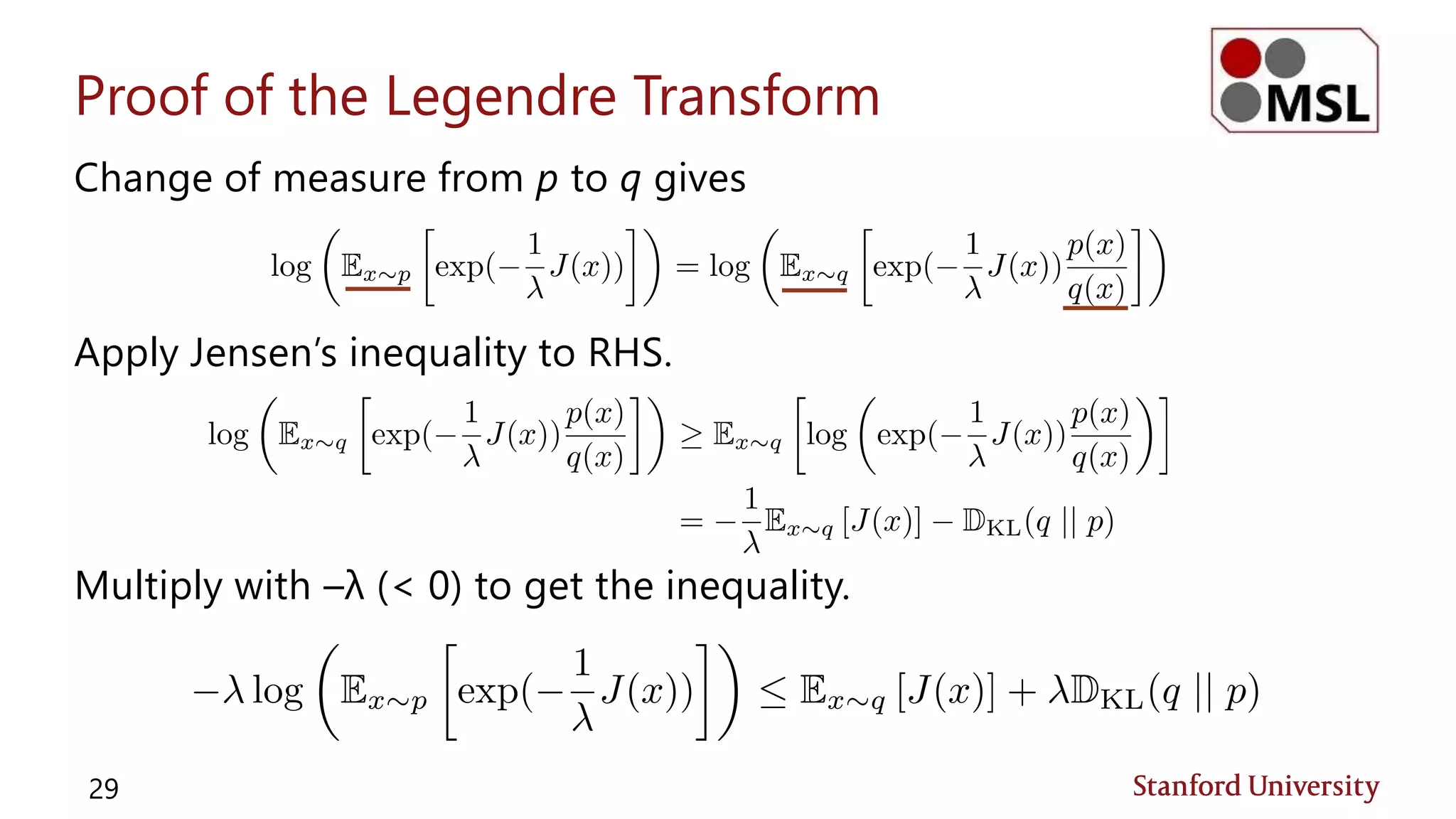
- 30. Jensen’s Inequality (Review) Let f be a convex function over a real-valued random variable X. Then, Furthermore, if f is strictly convex, the equality holds if and only if X = E[X] with probability 1, in which case X is a deterministic constant. In our case, log() is a strictly concave function, so the direction of the inequality is flipped. 30
- 31. Interpretations of the Legendre Transform • Think of x as a path in the state space rooted at the current state. • Think of J() as a cost over the path. • A path x is generated by a forward integration of an SDE defined by . As we vary the control input profile u, we change the resulting distribution over the state trajectories. 31
- 32. Interpretations of the Legendre Transform • LHS is independent of u, and is uniquely defined once the cost function J, the system dynamics and λ are specified. It is a property of the system and called the (Helmholtz) free energy. • The first term in RHS is the expected state-dependent cost. • The second term is non-negative since KL-divergence is non- negative. It turns out that this is an implicit measure of the control effort. 32
- 33. Interpretations of the Legendre Transform • LHS is independent of u, and is uniquely defined once the cost function J, the system dynamics and λ are specified. It is a property of the system and called the (Helmholtz) free energy. • The first term in RHS is the expected state-dependent cost. • The second term is non-negative since KL-divergence is non- negative. It turns out that this is an implicit measure of the control effort. 33
- 34. Interpretations of the Legendre Transform • LHS is independent of u, and is uniquely defined once the cost function J, the system dynamics and λ are specified. It is a property of the system and called the (Helmholtz) free energy. • The first term in RHS is the expected state-dependent cost. • The second term is non-negative since KL-divergence is non- negative. It turns out that this is an implicit measure of the control effort. 34
- 35. Optimality in the Legendre Sense The free energy is the solution to the following optimization problem. The optimal distribution is given by 35 Note: q is assumed to be absolutely continuous w.r.t. p.
- 36. Remarks • As we will see later, the KL-divergence is an implicit measure of the control cost weighted by λ. We see that the control cost naturally emerges out of the Legendre transform. • Questions that we might have at this moment: • Why is the minimizer called the free energy? Where does it come from? • How is it related to the Bellman’s principle of optimality? Are they the same? • How can we develop algorithms based on the information-theoretic control framework? To be continued… 36
- 37. References • H. J. Kappen, An Introduction to Stochastic Control Theory, Path Integrals and Reinforcement Learning, AIP Conference Proceedings, 2007. • H. J. Kappen, Path Integrals and Symmetry Breaking for Optimal Control Theory, Journal of Statistical MechanicsL Theory and Experiment, 2005. • E. A. Theodorou, Nonlinear Stochastic Control and Information Theoretic Dualities: Connections, Interdependencies and Thermodynamic Interpretations, Entropy, 2015. • G. Williams, P. Drews, B. Goldfain, J. M. Rehg, E. A. Theodorou, Information Theoretic Model Predictive Control: Theory and Applications to Autonomous Driving, arXiv, 2017. • C. Shalizi, Diffusions and the Wiener Process, http://www.stat.cmu.edu/~cshalizi/754/notes/lecture-17.pdf, accessed on Nov. 10, 2017. 37
Editor's Notes
- 20pt \begin{aligned} & \underset{u(t_0 \rightarrow t_f)}{\text{minimize}} & & J\left(t_0, x_0, u(t_0 \rightarrow t_f)\right)\\ & \text{subject to} & & x(t_0) = x_0 \\ & & & \dot x(t) = f\left(t,x(t), u(t)\right) \end{aligned} J = \phi\left(x(t_f)\right) + \int_{t_0}^{t_f} c\left(t,x(t),u(t)\right) dt u(t_0 \rightarrow t_f): [t_0, t_f] \rightarrow U
- 16pt \begin{aligned} \dot{x^*}(t) &= H_\lambda\left(t,x^*(t),u^*(t),\lambda(t)\right)\\ -\dot\lambda(t) &= H_x\left(t,x^*(t),u^*(t),\lambda(t)\right)\\ u^*(t) &= \arg\min_u H\left(t,x^*(t),u(t),\lambda(t)\right) \end{aligned} In the presence of Wiener noise, the PMP formalism can be generalized and yeilds a set of coupled stochastic differential equations, but they become difficult to solve due to the boundary conditions at initial and final time. In contrast, the inclusion of noise in the HJB framework is mathematically quite straightforward.
- 20 pts V(t,x) \triangleq \min_{u(t \rightarrow t_f)} J\left(t,x,u(t \rightarrow t_f)\right) 16 pts \begin{aligned} V(t,x) &= \min_{u(t \rightarrow t_f)} \left(\phi(x(t_f)) + \int_t^{t+dt} c(\tau,x(\tau),u(\tau))d\tau + \int_{t+dt}^{t_f} c(\tau,x(\tau),u(\tau))d\tau\right) \\ &= \min_{u(t \rightarrow t+dt)} \left(\int_t^{t+dt} c(\tau,x(\tau),u(\tau))d\tau + \min_{u({t+dt}\rightarrow t_f)} \left(\phi(x(t_f)) + \int_{t+dt}^{t_f} c(\tau,x(\tau),u(\tau))d\tau\right)\right) \end{aligned}
- 20 pts V(t+dt,x(t+dt)) = V(t,x) + V_t(t,x)dt + V_x(t,x)dx + o(dt) 16 pts V(t,x) = \min_{u(t \rightarrow t+dt)} \left(\int_t^{t+dt} c(\tau,x(\tau),u(\tau))d\tau + V(t,x) + V_t(t,x)dt + V_x(t,x)f(t,x,u)dt + o(dt) \right) 20 pts -V_t(t,x) = \min_{u} \left(c(t,x,u) + V_x(t,x)f(t,x,u) \right)
- 20 pts V(t_f, x({t_f})) = \phi(x(t_f)) 20 pts u^*(t,x) = \arg\min_u \left(c(t,x,u) + V_x(t,x) f(t,x,u)\right)
- 20 pts \begin{aligned} & \underset{u(t_0 \rightarrow t_f)}{\text{minimize}} & & \mathbb{E}_{x_0 \rightarrow x(t_f)} \left[J\left(t_0, x_0, u(t_0 \rightarrow t_f)\right)\right]\\ & \text{subject to} & & x(t_0) = x_0 \\ & & & dx = f\left(t,x(t), u(t)\right)dt + b(x(t))dw_t \end{aligned}
- I
- dx = f\left(t,x(t), u(t)\right)dt + b(x(t))dw_t
- Image URL: https://github.com/matthewfieger/wiener_process
- 20 pts dw_t \sim \mathcal{N}(0,dt)
- 16 pts w' = \lim_{t\rightarrow t_0} \frac{w_t - w_{t_0}}{t - t_0} \forall \epsilon > 0 \exist \delta > 0 t\in [t_0 - \delta, \t_0 + \delta] \Longrightarrow |\frac{w_t - w_{t_0}} \forall ~\epsilon > 0 ~\exists \delta > 0 ~~t \in [t_0 - \delta, t_0 + \delta] \Longrightarrow \left\lvert\frac{w_t - w_{t_0}}{t - t_0} - w'\right\lvert \leq \epsilon w_t - w_{t_0} \sim \mathcal{N}(0,t-t_0) \frac{w_t - w_{t_0}}{t - t_0} \sim \mathcal{N}(-w',\frac{1}{t-t_0})
- 20 pts V(t,x) \triangleq \min_{u(t \rightarrow t_f)} J\left(t,x,u(t \rightarrow t_f)\right) 16 pts \begin{aligned} V(t,x) &= \min_{u(t \rightarrow t_f)} \left(\phi(x(t_f)) + \int_t^{t+dt} c(\tau,x(\tau),u(\tau))d\tau + \int_{t+dt}^{t_f} c(\tau,x(\tau),u(\tau))d\tau\right) \\ &= \min_{u(t \rightarrow t+dt)} \left(\int_t^{t+dt} c(\tau,x(\tau),u(\tau))d\tau + \min_{u({t+dt}\rightarrow t_f)} \left(\phi(x(t_f)) + \int_{t+dt}^{t_f} c(\tau,x(\tau),u(\tau))d\tau\right)\right) \end{aligned}
- 20 pts V(t,x) = \min_{u(t \rightarrow t + dt)}\mathbb{E}_{x \rightarrow x(t_f)} \left[ \int_t^{t+dt} c\left(\tau,x(\tau),u(\tau)\right) d\tau + V\left(t+dt,x(t+dt)\right)\right]
- 20 pts \mathbb{E}\left[V(t+dt,x(t+dt))\right] = V(t,x) + V_t(t,x)dt + V_x(t,x)\mathbb{E}[dx] + \frac{1}{2} V_{x^2}(t,x)\mathbb{E}[dx^2] + o(dt) \mathbb{E}[dx^2] = f^2dt^2 + 2fb\mathbb{E}[dw_t]dt + b^2\mathbb{E}[dw_t^2]
- 20 pts \mathbb{E}\left[V(t+dt,x(t+dt))\right] = V(t,x) + V_t(t,x)dt + V_x(t,x) f(t,x(t),u(t)) + \frac{1}{2} V_{x^2}(t,x)\mathbb{E}[dx^2] + o(dt) \mathbb{E}[dx^2] = f^2dt^2 + 2fb\mathbb{E}[dw_t]dt + b^2\mathbb{E}[dw_t^2] \begin{aligned} dx &= \mu dt + \sigma dw_t \\ df(t,x) &= \left(f_t + f_x\mu + \frac{1}{2}\sigma^2 f_{x^2}\right)dt + \sigma f_x dw_t \end{aligned}
- -V_t(t,x) = \min_u\left(c(t,x,u) + V_x(t,x) f(t,x,u) + \frac{1}{2} V_{x^2}(t,x)b^2(x)\right)
- 20 pts -V_t(t,x) = \min_u\left(c(x,u,t) + V_x^{\mathrm{T}}(t,x) f(t,x,u) + \frac{1}{2} \mathrm{tr}\left(V_{xx}(t,x)B(x)B(x)^\mathrm{T}\right)\right) LQ control problem. A notable exception is when b is linear in x and c is quadratic in x and u. The solution for V(t,x) is quadratic in x with time-varying coefficients. These coefficients satisfy coupled ODEs (Riccati equations) that can be solved efficiently.
- A notable exception is when b is linear in x and c is quadratic in x and u. The solution for V(t,)
- 20 pts x \in \Omega J(\cdot): \Omega \rightarrow \mathbb{R} \lambda > 0 -\lambda \log\left(\mathbb{E}_{x\sim p} \left[\exp(-\frac{1}{\lambda} J(x))\right]\right) \leq \mathbb{E}_{x\sim q} \left[J(x)\right] + \lambda \mathbb{D}_{\mathrm{KL}}(q \mid\mid p)
- 16 pts \log\left(\mathbb{E}_{x\sim p} \left[\exp(-\frac{1}{\lambda} J(x))\right]\right) = \log\left(\mathbb{E}_{x\sim q} \left[\exp(-\frac{1}{\lambda} J(x)) \frac{p(x)}{q(x)}\right]\right) \begin{aligned} \log\left(\mathbb{E}_{x\sim q} \left[\exp(-\frac{1}{\lambda} J(x)) \frac{p(x)}{q(x)}\right]\right) &\geq \mathbb{E}_{x \sim q} \left[ \log\left(\exp(-\frac{1}{\lambda} J(x)) \frac{p(x)}{q(x)}\right)\right] \\ &= -\frac{1}{\lambda} \mathbb{E}_{x\sim q} \left[J(x)\right] - \mathbb{D}_{\mathrm{KL}} (q \sim \sim p) \end{aligned}
- \mathbb{E}[f(X)] \geq f(\mathbb{E}[X])
- \begin{aligned} & \underset{q(x;u)}{\text{minimize}} & & \mathbb{E}_{x \sim q} \left[J(x)\right] + \lambda \mathbb{D}_{\mathrm{KL}} (q \mid\mid p)\\ & \text{subject to} & & \int q(x;u) dx = 1\\ & & & \forall x > 0 ~ q(x;u) \geq 0 \\ \end{aligned}