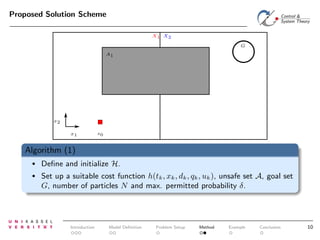
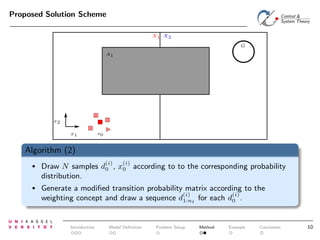
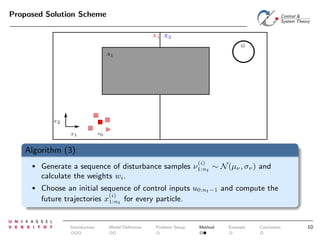
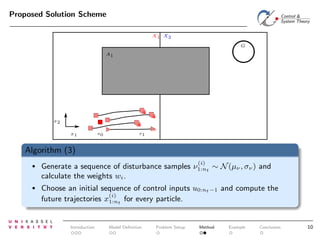
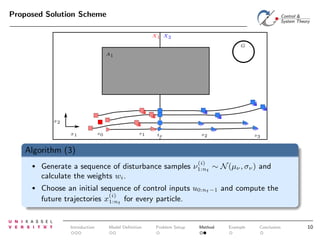
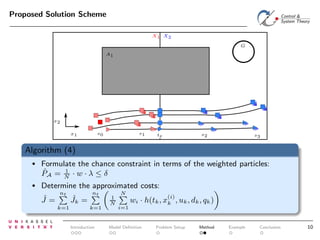
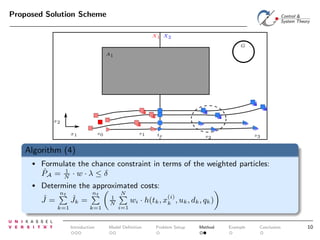
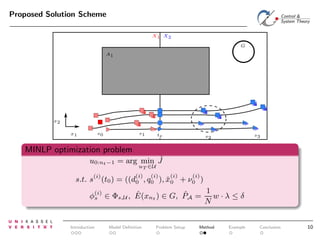
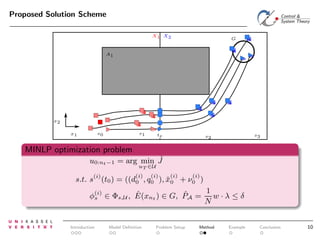
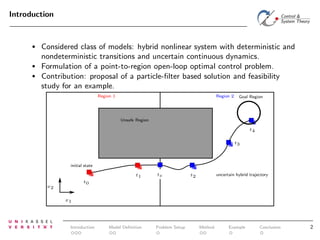
The document discusses controlling uncertain hybrid nonlinear systems using a particle filter-based approach for robust optimal control. It outlines the formulation of a point-to-region open-loop control problem and describes the 'jump markov nonlinear hybrid automaton' model that incorporates both deterministic and stochastic elements. The proposed method aims to minimize the probability of entering unsafe states while achieving performance goals under uncertainties.

1. Control of Uncertain Hybrid Nonlinear Systems
Using Particle Filters
Leonhard Asselborn
Martin Jilg
Olaf Stursberg
Institute of Control and System Theory
University of Kassel
l.asselborn@uni-kassel.de
martin.jilg@uni-kassel.de
stursberg@uni-kassel.de
www.control.eecs.uni-kassel.de

2. Introduction
•
•
•
Considered class of models: hybrid nonlinear system with deterministic and
nondeterministic transitions and uncertain continuous dynamics.
Formulation of a point-to-region open-loop optimal control problem.
Contribution: proposal of a particle-filter based solution and feasibility
study for an example.
Introduction
Model Definition
Problem Setup
Method
Example
Conclusion
2

3. Introduction
•
•
•
Considered class of models: hybrid nonlinear system with deterministic and
nondeterministic transitions and uncertain continuous dynamics.
Formulation of a point-to-region open-loop optimal control problem.
Contribution: proposal of a particle-filter based solution and feasibility
study for an example.
Region 1
Region 2
Goal Region
Unsafe Region
t4
t3
initial state
t1
te
uncertain hybrid trajectory
t2
t0
x2
x1
Introduction
Model Definition
Problem Setup
Method
Example
Conclusion
2

4. Stochastic Hybrid Models (1)
•
Stochastic hybrid models are a suitable tool for a wide range of processes
Introduction
Model Definition
Problem Setup
Method
Example
Conclusion
3

5. Stochastic Hybrid Models (1)
•
Stochastic hybrid models are a suitable tool for a wide range of processes
•
Three main representations of Stochastic hybrid models in literature
1. Stochastic Hybrid Systems (SHS)
◮
Randomness only in the continuous dynamics
2. Switching Diffusion Processes (SDP)
◮
Random cont. dynamics and spontaneous transitions according to a Poisson
process
3. Piecewise Deterministic Markov Processes (PDMP)
◮
Deterministic continuous dynamics and spontaneous or autonomous transitions
according to a Poisson Process and state space partitions, respectively.
Introduction
Model Definition
Problem Setup
Method
Example
Conclusion
3

6. Stochastic Hybrid Models (2)
Control methods for Stochastic Hybrid Models in the literature (as far as
relevant for this paper):
Method specification
optimal
control
[1]
particle
filter
chance
constraints
nonlinear
dynamics
-
-
[2]
Model specification
uncertain
dynamics
-
-
[3]
-
[4]
[6]
[1]:
[2]:
[3]:
[4]:
[5]:
[6]:
-
-
-
-
[5]
stochastic deterministic
events
events
-
-
-
-
-
-
-
-
-
-
Bemporad et. al.: Model-Predictive Control of Discrete Hybrid Stochastic Automata, 2011,
Blackmore et. al.: Optimal Robust Predictive Control of Nonlinear Systems under Probabilistic Uncertainty using Particles, 2007,
Adamek et. al.: Stochastic Optimal Control for Hybrid Systems with Uncertain Dynamics, 2008,
Ding et. al.: Increasing Efficiency of Optimization-based Path Planning for Robotic Manipulators, 2011,
Li et. al.: Risk-Sensitive Cubature Filtering for Jump Markov Nonlinear Systems and Its Application to Land Vehicle Positioning, 2011,
Vitus et. al.: Closed-Loop Belief Space Planning for Linear, Gaussian Systems, 2011
Introduction
Model Definition
Problem Setup
Method
Example
Conclusion
4

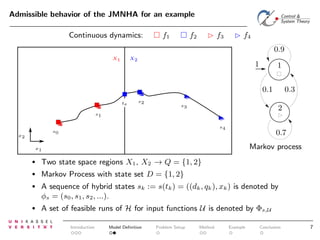
7. Considered Class of Model
The “Jump Markov Nonlinear Hybrid Automaton (JMNHA)”:
• No resets in the continuous state variable for autonomous transitions
based on a state space partition
•
Spontaneous transitions according to a Markov Process.
•
Uncertain nonlinear dynamics: deterministic behavior for t ∈]tk , tk+1 [,
stochastic pertubation at tk .
→ Model simplification by evaluating the nondeterministic events in discrete
time.
Introduction
Model Definition
Problem Setup
Method
Example
Conclusion
5

8. Considered Class of Model
The “Jump Markov Nonlinear Hybrid Automaton (JMNHA)”:
• No resets in the continuous state variable for autonomous transitions
based on a state space partition
•
Spontaneous transitions according to a Markov Process.
•
Uncertain nonlinear dynamics: deterministic behavior for t ∈]tk , tk+1 [,
stochastic pertubation at tk .
PDMP
→ Model simplification by evaluating the nondeterministic events in discrete
time.
Introduction
Model Definition
Problem Setup
Method
Example
Conclusion
5

9. Considered Class of Model
The “Jump Markov Nonlinear Hybrid Automaton (JMNHA)”:
• No resets in the continuous state variable for autonomous transitions
based on a state space partition
•
Spontaneous transitions according to a Markov Process.
•
Uncertain nonlinear dynamics: deterministic behavior for t ∈]tk , tk+1 [,
stochastic pertubation at tk .
PDMP
→ Model simplification by evaluating the nondeterministic events in discrete
time.
Introduction
Model Definition
Problem Setup
Method
Example
Conclusion
5

10. Considered Class of Model
The “Jump Markov Nonlinear Hybrid Automaton (JMNHA)”:
• No resets in the continuous state variable for autonomous transitions
based on a state space partition
•
Spontaneous transitions according to a Markov Process.
•
Uncertain nonlinear dynamics: deterministic behavior for t ∈]tk , tk+1 [,
stochastic pertubation at tk .
PDMP
→ Model simplification by evaluating the nondeterministic events in discrete
time.
Introduction
Model Definition
Problem Setup
Method
Example
Conclusion
5

11. Considered Class of Model
The “Jump Markov Nonlinear Hybrid Automaton (JMNHA)”:
• No resets in the continuous state variable for autonomous transitions
based on a state space partition
•
Spontaneous transitions according to a Markov Process.
•
Uncertain nonlinear dynamics: deterministic behavior for t ∈]tk , tk+1 [,
stochastic pertubation at tk .
PDMP
JMNHA
→ Model simplification by evaluating the nondeterministic events in discrete
time.
Introduction
Model Definition
Problem Setup
Method
Example
Conclusion
5

12. Considered Class of Model
The “Jump Markov Nonlinear Hybrid Automaton (JMNHA)”:
• No resets in the continuous state variable for autonomous transitions
based on a state space partition
•
Spontaneous transitions according to a Markov Process.
•
Uncertain nonlinear dynamics: deterministic behavior for t ∈]tk , tk+1 [,
stochastic pertubation at tk .
xk+1
PDMP
xk
xk+1 = xk +
tk+1
t
f (τ )dτ + νk
k
JMNHA
→ Model simplification by evaluating the nondeterministic events in discrete
time.
Introduction
Model Definition
Problem Setup
Method
Example
Conclusion
5

13. A class of Stochastic Hybrid Systems
Definition 1:
A Jump Markov Nonlinear Hybrid Automaton is defined by
H = (T, Tk , Z, X, U, U, f, ψq , ψd , ν)
with t ∈ T , tk ∈ Tk
•
nonlinear continuous dynamics x = f (x, u, d, q), x(t) ∈ X, u(t) ∈ U ,
˙
d(tk ) ∈ D, q(tk ) ∈ Q
•
hybrid state space S = X × Z, x ∈ X, z = (d, q) ∈ Z
•
update function ψq : X × X → 2Q for the state space region
•
update function ψd : D × D → [0, 1]nd for the Markov process
•
uncertainty ν in the continuous state variable x, xk+1 = xk+1 + νk+1
ˇ
Introduction
Model Definition
Problem Setup
Method
Example
Conclusion
6

14. Admissible behavior of the JMNHA for an example
Continuous dynamics:
f1
f2
⊲ f3
⊲ f4
0.9
X1
X2
1
1
0.1
0.3
2
0.7
x2
Markov process
x1
•
Two state space regions X1 , X2 → Q = {1, 2}
•
Markov Process with state set D = {1, 2}
•
A sequence of hybrid states sk := s(tk ) = ((dk , qk ), xk ) is denoted by
φs = (s0 , s1 , s2 , ...).
•
A set of feasible runs of H for input functions U is denoted by Φs,U
Introduction
Model Definition
Problem Setup
Method
Example
Conclusion
7

15. Admissible behavior of the JMNHA for an example
Continuous dynamics:
f1
f2
⊲ f3
⊲ f4
0.9
X1
X2
1
1
0.1
te
s2
s3
0.3
2
s1
s4
s0
x2
0.7
Markov process
x1
•
Two state space regions X1 , X2 → Q = {1, 2}
•
Markov Process with state set D = {1, 2}
•
A sequence of hybrid states sk := s(tk ) = ((dk , qk ), xk ) is denoted by
φs = (s0 , s1 , s2 , ...).
•
A set of feasible runs of H for input functions U is denoted by Φs,U
Introduction
Model Definition
Problem Setup
Method
Example
Conclusion
7

16. Robust Optimal Control Problem
The goal of the proposed method is to control H in an optimal manner w.r.t.
chance, input and state constraints.
Introduction
Model Definition
Problem Setup
Method
Example
Conclusion
8

17. Robust Optimal Control Problem
The goal of the proposed method is to control H in an optimal manner w.r.t.
chance, input and state constraints.
•
Perfomance index: Jφs =
Introduction
nt
k=1
Model Definition
h(tk , xk , dk , qk , uk )
Problem Setup
Method
Example
Conclusion
8

18. Robust Optimal Control Problem
The goal of the proposed method is to control H in an optimal manner w.r.t.
chance, input and state constraints.
•
•
Perfomance index: Jφs = nt h(tk , xk , dk , qk , uk )
k=1
Unsafe sets: A := ∪na Ai ⊂ X
i=1
Introduction
Model Definition
Problem Setup
Method
Example
Conclusion
8

19. Robust Optimal Control Problem
The goal of the proposed method is to control H in an optimal manner w.r.t.
chance, input and state constraints.
•
•
•
Perfomance index: Jφs = nt h(tk , xk , dk , qk , uk )
k=1
Unsafe sets: A := ∪na Ai ⊂ X
i=1
A maximally permitted probability for entering an unsafe set: δ
Introduction
Model Definition
Problem Setup
Method
Example
Conclusion
8

20. Robust Optimal Control Problem
The goal of the proposed method is to control H in an optimal manner w.r.t.
chance, input and state constraints.
•
•
•
•
Perfomance index: Jφs = nt h(tk , xk , dk , qk , uk )
k=1
Unsafe sets: A := ∪na Ai ⊂ X
i=1
A maximally permitted probability for entering an unsafe set: δ
Goal set: G ⊂ X
Introduction
Model Definition
Problem Setup
Method
Example
Conclusion
8

21. Robust Optimal Control Problem
The goal of the proposed method is to control H in an optimal manner w.r.t.
chance, input and state constraints.
•
•
•
•
Perfomance index: Jφs = nt h(tk , xk , dk , qk , uk )
k=1
Unsafe sets: A := ∪na Ai ⊂ X
i=1
A maximally permitted probability for entering an unsafe set: δ
Goal set: G ⊂ X
Problem Definition
min E(Jφs )
uT ∈U
s.t. s(t0 ) = ((d0 , q0 ), x0 + ν0 )
φs ∈ Φs,U
x(tf ) ∈ G
P rob(xT,φs ∈ A for any t ∈ T ) ≤ δ
Introduction
Model Definition
Problem Setup
Method
Example
Conclusion
8

22. Approximation by Particle Filters
The main properties of a Particle Filter
1
1
[2]: L. Blackmore, B. C. Williams: Optimal Robust Predictive Control of Nonlinear Systems
under Probabilistic Uncertainty using Particles, 2007
Introduction
Model Definition
Problem Setup
Method
Example
Conclusion
9

23. Approximation by Particle Filters
The main properties of a Particle Filter
1
•
A particle represents a sample of a random variable Ξ drawn from a given
probability distribution: ξ (1) , . . . , ξ (N)
•
The expected value can be approximated by the sample mean:
N
1
(i)
ˆ
E(Ξ) = N
i=1 ξ
•
Each particle represents a deterministic realization of the JMNHA over a finite
horizon.
1
[2]: L. Blackmore, B. C. Williams: Optimal Robust Predictive Control of Nonlinear Systems
under Probabilistic Uncertainty using Particles, 2007
Introduction
Model Definition
Problem Setup
Method
Example
Conclusion
9

24. Approximation by Particle Filters
The main properties of a Particle Filter
1
•
A particle represents a sample of a random variable Ξ drawn from a given
probability distribution: ξ (1) , . . . , ξ (N)
•
The expected value can be approximated by the sample mean:
N
1
(i)
ˆ
E(Ξ) = N
i=1 ξ
•
Each particle represents a deterministic realization of the JMNHA over a finite
horizon.
The particles are used to transform a stochastic optimization problem into
a deterministic variant.
1
[2]: L. Blackmore, B. C. Williams: Optimal Robust Predictive Control of Nonlinear Systems
under Probabilistic Uncertainty using Particles, 2007
Introduction
Model Definition
Problem Setup
Method
Example
Conclusion
9

25. Approximation by Particle Filters
The main properties of a Particle Filter
1
•
A particle represents a sample of a random variable Ξ drawn from a given
probability distribution: ξ (1) , . . . , ξ (N)
•
The expected value can be approximated by the sample mean:
N
1
(i)
ˆ
E(Ξ) = N
i=1 ξ
•
Each particle represents a deterministic realization of the JMNHA over a finite
horizon.
The particles are used to transform a stochastic optimization problem into
a deterministic variant.
The setup of a chance constraint
(i)
•
Indicator function 1A (x1:nt ) denotes if the i-th trajectory is in A at any time.
•
Binary vector λ ∈ {0, 1}N×1 is used for a mixed integer formulation:
1
ˆ
PA = N · w · λ ≤ δ with weighting vector w.
1
[2]: L. Blackmore, B. C. Williams: Optimal Robust Predictive Control of Nonlinear Systems
under Probabilistic Uncertainty using Particles, 2007
Introduction
Model Definition
Problem Setup
Method
Example
Conclusion
9

26. Proposed Solution Scheme
X1 X2
G
A1
x2
x1
s0
Algorithm (1)
•
Define and initialize H.
•
Set up a suitable cost function h(tk , xk , dk , qk , uk ), unsafe set A, goal set
G, number of particles N and max. permitted probability δ.
Introduction
Model Definition
Problem Setup
Method
Example
Conclusion
10

27. Proposed Solution Scheme
X1 X2
G
A1
x2
x1
s0
Algorithm (2)
(i)
(i)
•
Draw N samples d0 , x0 according to to the corresponding probability
distribution.
•
Generate a modified transition probability matrix according to the
(i)
(i)
weighting concept and draw a sequence d1:nt for each d0 .
Introduction
Model Definition
Problem Setup
Method
Example
Conclusion
10

28. Proposed Solution Scheme
X1 X2
G
A1
x2
x1
s0
Algorithm (3)
(i)
•
Generate a sequence of disturbance samples ν1:nt ∼ N (µν , σν ) and
calculate the weights wi .
•
Choose an initial sequence of control inputs u0:nt −1 and compute the
(i)
future trajectories x1:nt for every particle.
Introduction
Model Definition
Problem Setup
Method
Example
Conclusion
10

29. Proposed Solution Scheme
X1 X2
G
A1
x2
x1
s0
s1
Algorithm (3)
(i)
•
Generate a sequence of disturbance samples ν1:nt ∼ N (µν , σν ) and
calculate the weights wi .
•
Choose an initial sequence of control inputs u0:nt −1 and compute the
(i)
future trajectories x1:nt for every particle.
Introduction
Model Definition
Problem Setup
Method
Example
Conclusion
10

30. Proposed Solution Scheme
X1 X2
G
A1
x2
x1
s0
s1
te
s2
s3
Algorithm (3)
(i)
•
Generate a sequence of disturbance samples ν1:nt ∼ N (µν , σν ) and
calculate the weights wi .
•
Choose an initial sequence of control inputs u0:nt −1 and compute the
(i)
future trajectories x1:nt for every particle.
Introduction
Model Definition
Problem Setup
Method
Example
Conclusion
10

31. Proposed Solution Scheme
X1 X2
G
A1
x2
s1
s0
x1
s2
te
s3
Algorithm (4)
•
Formulate the chance constraint in terms of the weighted particles:
1
ˆ
PA = N · w · λ ≤ δ
•
Determine the approximated costs:
ˆ
J=
nt
k=1
ˆ
Jk =
nt
k=1
Introduction
1
N
N
i=1
(i)
wi · h(tk , xk , uk , dk , qk )
Model Definition
Problem Setup
Method
Example
Conclusion
10

32. Proposed Solution Scheme
X1 X2
G
A1
x2
s1
s0
x1
te
s3
s2
Algorithm (4)
•
Formulate the chance constraint in terms of the weighted particles:
1
ˆ
PA = N · w · λ ≤ δ
•
Determine the approximated costs:
ˆ
J=
nt
k=1
ˆ
Jk =
nt
k=1
Introduction
1
N
N
i=1
(i)
wi · h(tk , xk , uk , dk , qk )
Model Definition
Problem Setup
Method
Example
Conclusion
10

33. Proposed Solution Scheme
X1 X2
G
A1
x2
s1
s0
x1
te
s3
s2
MINLP optimization problem
ˆ
u0:nt −1 = arg min J
uT ∈U
(i)
s.t. s (t0 ) =
(i)
(i)
(i)
((d0 , q0 ), x0
ˇ
(i)
+ ν0 )
1
ˆ
ˆ
φ(i) ∈ Φs,U , E(xnt ) ∈ G, PA = w · λ ≤ δ
s
N
Introduction
Model Definition
Problem Setup
Method
Example
Conclusion
10

34. Proposed Solution Scheme
X1 X2
G
A1
x2
s1
s0
x1
te
s3
s2
MINLP optimization problem
ˆ
u0:nt −1 = arg min J
uT ∈U
(i)
s.t. s (t0 ) =
(i)
(i)
(i)
((d0 , q0 ), x0
ˇ
(i)
+ ν0 )
1
ˆ
ˆ
φ(i) ∈ Φs,U , E(xnt ) ∈ G, PA = w · λ ≤ δ
s
N
Introduction
Model Definition
Problem Setup
Method
Example
Conclusion
10

35. Trajectory planning for a ground vehicle
•
•
•
vehicle accelerates to
maximum speed
trajectory
start
25
vehicle turns left and stays
close to the obstacle
stop
goal
particles
isocost lines
vehicle decelerates in front
of the goal
20
particles lead to many
trajectories with steering
and braking failure due to
the weighting concept
15
•
at most 1 of the 10
particle trajectories cross
the obstacle
•
η
•
MINLP was solved with an
SQP method within a
Branch-and-Bound
environment.
Introduction
Model Definition
10
5
−2
0
2
Problem Setup
4
6
Method
8
ζ
10
12
Example
14
16
Conclusion
18
11

36. Conclusion
Conclusion
Summary:
•
Introduction of an uncertain nonlinear hybrid system.
•
Presentation of an algorithm for optimal open-loop control.
•
A numerical example showed the results of the proposed method.
Remarks:
•
Scheme generates a probabilistically safe sub-optimal trajectory
•
Computationally expensive due to the complex model class and the
challenging problem.
•
Branch-and-Bound may cut off branches which contain feasible solutions.
Future work:
•
Efficient encoding of the chance constraints and alternatives for solving
the optimization.
•
Theoretical analysis concerning the convergence of the approximated
optimization problem.
Introduction
Model Definition
Problem Setup
Method
Example
Conclusion
12