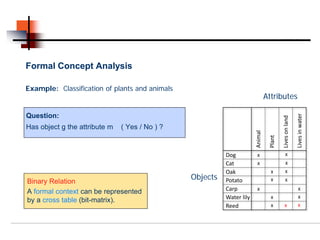
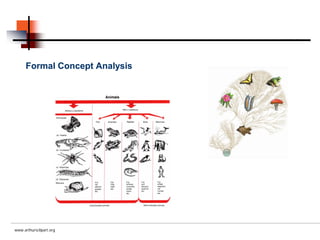
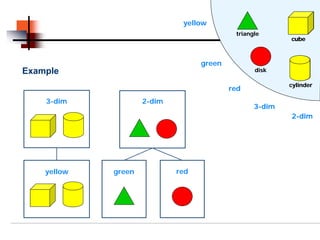
Cat x x A⊂G A′ ⊂ M Oak x x Potato x x Formal concept analysis studies how objects can be grouped hierarchically based on their common attributes. It models concepts as units consisting of an extension (objects belonging to the concept) and an intension (attributes common to those objects). Formal contexts represent relationships between objects and attributes, and derivation operators identify the attributes common to a group of objects or the objects sharing a group of attributes.

1. Summer School
“Achievements and Applications of Contemporary Informatics,
Mathematics and Physics” (AACIMP 2011)
August 8-20, 2011, Kiev, Ukraine
̶ Formal Concept Analysis ̶
Erik Kropat
University of the Bundeswehr Munich
Institute for Theoretical Computer Science,
Mathematics and Operations Research
Neubiberg, Germany

2. Formal Concept Analysis
Formal Concept Analysis studies, how objects can be hierarchically grouped together
according to their common attributes.
Tree of Life
Source: Tree of Life Web Project
http://tolweb.org/tree/

3. Formal Concept Analysis
www.arthursclipart.org

4. What is a “concept” ?
A concept is a cognitive unit of meaning or a unit of knowledge.
Concept Bird
properties − feathered − warm-blooded
− winged − egg-laying
− bipedal − vertebrate
objects
blackbird, sparrow, raven,…

5. Formal Concept Analysis
• . . . is a powerful tool for data analysis, information retrieval,
and knowledge discovery in large databases.
• . . . is a conceptual clustering method,
which clusters simultaneously objects and their properties.
• . . . can mathematically represent, identify and analyze green yellow
conceptual structures.
red
2-dim
cylinder
disk
3-dim
triangle
cube

6. yellow
triangle
cube
green
Example disk
cylinder
red
3-dim 2-dim
3-dim
2-dim
yellow green red

7. Formal Concept Analysis
• . . . models concepts as units of thought, consisting of two parts:
− extension = objects belonging to the concept
− intension = attributes common to all those objects.
• . . . is an exploratory data analysis technique for discovering new knowledge.
• . . . can be used for efficiently computing association rules
applied in decision support systems.
• . . . can extract and visualize hierarchies !!!

8. Formal Concept Analysis
Goal: Derive automatically an ontology from a – very large – collection of objects
and their properties or features.
Target Marketing
Set of objects ⇒ clusters of objects
customers
correspond
⇔
one-for-one
Set of attributes
age, sex, income level, ⇒ clusters of attributes
spending habits, …
predict customer purchase decisions /
⇒ recommend products to customers

9. Sensitive advertisement
clusters of objects
correspond
one-for-one
clusters of attributes

10. Formal Contexts

11. Example: Classification of plants and animals
Animal
Dog Cat
Plant
lives on land
Reed Water lily Oak
lives in water
Carp Potato
Objects Attributes

12. Formal Concept Analysis
Example: Classification of plants and animals
Attributes
Question:
Lives in water
Lives on land
Has object g the attribute m ( Yes / No ) ?
Animal
Plant
Dog x x
Cat x x
Oak x x
Binary Relation
Objects Potato x x
A formal context can be represented Carp x x
Water lily x x
by a cross table (bit-matrix).
Reed x x x

13. Formal Context
A formal context describes the relation between
objects and attributes.
A formal context (G, M, I) consists of
a set G of objects,
a set M of attributes and
a binary relation I ⊂ G x M.
Has object g the attribute m ( yes / no ) ?

14. Notation
• g I m means: “object g has attribute m”.
Example: (a) dog I animal
(b) carp I lives in water

15. Derivation Operators

16. The Derivation Operators (Type I)
A ⊂ G selection of objects.
Question: Which attributes from M are common to all these objects?
Lives in water
Set of common attributes of the objects in A
Lives on land
A’ := A↑:= { m ∈ M | g I m for all g ∈ A }
Animal
Plant
Dog x x
Cat x x
A⊂G A′ ⊂ M Oak x x
Potato x x
{Dog, Cat} Carp x x
{Oak, Potato} Water lily x x
Reed x x x

17. The Derivation Operators (Type I)
A ⊂ G selection of objects.
Question: Which attributes from M are common to all these objects?
Lives in water
Set of common attributes of the objects in A
Lives on land
A’ := A↑:= { m ∈ M | g I m for all g ∈ A }
Animal
Plant
Dog x x
Cat x x
A⊂G A′ ⊂ M Oak x x
Potato x x
{Dog, Cat} {Animal, lives on land} Carp x x
{Oak, Potato} Water lily x x
Reed x x x

18. The Derivation Operators (Type I)
A ⊂ G selection of objects.
Question: Which attributes from M are common to all these objects?
Lives in water
Set of common attributes of the objects in A
Lives on land
A’ := A↑:= { m ∈ M | g I m for all g ∈ A }
Animal
Plant
Dog x x
Cat x x
A⊂G A′ ⊂ M Oak x x
Potato x x
{Dog, Cat} {Animal, lives on land} Carp x x
{Oak, Potato} Water lily x x
Reed x x x

19. The Derivation Operators (Type I)
A ⊂ G selection of objects.
Question: Which attributes from M are common to all these objects?
Lives in water
Set of common attributes of the objects in A
Lives on land
A’ := A↑:= { m ∈ M | g I m for all g ∈ A }
Animal
Plant
Dog x x
Cat x x
A⊂G A′ ⊂ M Oak x x
Potato x x
{Dog, Cat} {Animal, lives on land} Carp x x
{Oak, Potato} {Plant, lives on land} Water lily x x
Reed x x x

20. The Derivation Operators (Type II)
B ⊂ M a set of attributes.
Question: Which objects have all the attributes from B?
Lives in water
Set of objects that have all the attributes from B
Lives on land
B’ := B↓:= { g ∈ G | g I m for all m ∈ B }
Animal
Plant
Dog x x
Cat x x
B⊂M B′ ⊂ G Oak x x
Potato x x
{Plant, lives on land} Carp x x
{Animal, lives in water} Water lily x x
Reed x x x

21. The Derivation Operators (Type II)
B ⊂ M a set of attributes.
Question: Which objects have all the attributes from B?
Lives in water
Set of objects that have all the attributes from B
Lives on land
B’ := B↓:= { g ∈ G | g I m for all m ∈ B }
Animal
Plant
Dog x x
Cat x x
B⊂M B′ ⊂ G Oak x x
Potato x x
{Plant, lives on land} {Oak, Potato, Reed} Carp x x
{Animal, lives in water} Water lily x x
Reed x x x

22. The Derivation Operators (Type II)
B ⊂ M a set of attributes.
Question: Which objects have all the attributes from B?
Lives in water
Set of objects that have all the attributes from B
Lives on land
B’ := B↓:= { g ∈ G | g I m for all m ∈ B }
Animal
Plant
Dog x x
Cat x x
B⊂M B′ ⊂ G Oak x x
Potato x x
{Plant, lives on land} {Oak, Potato, Reed} Carp x x
{Animal, lives in water} Water lily x x
Reed x x x

23. The Derivation Operators (Type II)
B ⊂ M a set of attributes.
Question: Which objects have all the attributes from B?
Lives in water
Set of objects that have all the attributes from B
Lives on land
B’ := B↓:= { g ∈ G | g I m for all m ∈ B }
Animal
Plant
Dog x x
Cat x x
B⊂M B′ ⊂ G Oak x x
Potato x x
{Plant, lives on land} {Oak, Potato, Reed} Carp x x
{Animal, lives in water} {Carp} Water lily x x
Reed x x x

24. 1) If a selection of objects is enlarged,
Derivation Operators - Facts then
the attributes which are common
Let (G, M, I) be a formal context. to all objects of the larger selection
are among
A, A1, A2 ⊂ G sets of objects.
the common attributes of the smaller selection.
B, B1, B2 ⊂ G sets of attributes.
1) A1 ⊂ A2 ⇒ A′2 ⊂ A′1 1′) B1 ⊂ B2 ⇒ B′2 ⊂ B′1
2) A ⊂ A′′ 2′) B ⊂ B′′
3) A′ = A′′′ 3′) B′ = B′′′
4) A ⊂ B′ ⇔ B ⊂ A′ ⇔ A x B ⊂ I
The derivation operators constitute a Galois connection
between the power sets P(G) and P (M).

25. Formal Concepts

26. Formal Concepts
Formal Context: Defines a relation between objects and attributes.
Real World: Objects are characterized by particular attributes.
Object
Attributes

27. Formal Concepts
Let (G, M, I) be a formal context, where A ⊂ G and B ⊂ M.
(A, B) is a formal concept of (G, M, I), iff
A′ = B and B′ = A.
The set A is called the extent and
the set B is called the intent
of the formal concept (A, B).

28. Formal Concepts
• Extent A and intent B of a formal concept (A,B)
correspond to each other by the binary relation I of the underlying formal context.
• The description of a formal concept is redundant,
because each of the two parts determines the other
Extent Intent
(objects) (attributes)
Duality

29. How can we find “formal concepts”?
Lives in water
Lives on land
A formal concept (A, B) corresponds to a
Animal
Plant
filled rectangular subtable
with row set A and column set B. Dog x x
Cat x x
Oak x x
Potato x x
( {Dog, Cat}, {Animal, lives on land} ) Carp x x
Water lily x x
Reed x x x

30. How can we find “formal concepts”?
Lives in water
Lives on land
A formal concept (A, B) corresponds to a
Animal
Plant
filled rectangular subtable
with row set A and column set B. Dog x x
Cat x x
Oak x x
Potato x x
( {Dog, Cat}, {Animal, lives on land} ) Carp x x
Water lily x x
Reed x x x
Each of the two parts determines the other!

31. Exercise
Determine the sets of objects A and the set of attributes B
such that the pair (A, B) represents a formal concept.
(a) A = {oak, potato, reed}, B = ?
(b) A = ?, B = {animal, lives in water}

32. How can we find “formal concepts”?
Lives in water
Lives on land
A formal concept (A, B) corresponds to a
Animal
Plant
filled rectangular subtable
with row set A and column set B. Dog x x
Cat x x
Oak x x
Potato x x
( {Dog, Cat}, {Animal, lives on land} ) Carp x x
Water lily x x
Reed x x
( {Oak, Potato, Reed}, {Plant, lives on land} ) x

33. How can we find “formal concepts”?
Lives in water
Lives on land
A formal concept (A, B) corresponds to a
Animal
Plant
filled rectangular subtable
with row set A and column set B. Dog x x
Cat x x
Oak x x
Potato x x
( {Dog, Cat}, {Animal, lives on land} ) Carp x x
Water lily x x
Reed x x
( {Oak, Potato, Reed}, {Plant, lives on land} ) x
( {Carp}, {Animal, lives in water} )

34. How can we find “formal concepts”?
Lives in water
Lives on land
A formal concept (A, B) corresponds to a
Animal
Plant
filled rectangular subtable
with row set A and column set B. Dog x x
Cat x x
Oak x x
Potato x x
Question: Is the following pair a formal concept? Carp x x
Water lily x x
Reed x x x
( {Oak, Potato}, {Plant, lives on land} )

35. How can we find “formal concepts”?
Lives in water
Lives on land
A formal concept (A, B) corresponds to a
Animal
Plant
filled rectangular subtable
with row set A and column set B. Dog x x
Cat x x
Oak x x
Potato x x
Question: Is the following pair a formal concept? Carp x x
Water lily x x
Reed x x x
( {Oak, Potato}, {Plant, lives on land} )
There exist filled rectangular subtables that do not determine formal concepts

36. Computing all Formal Concepts
Lemma
Each formal concept (A, B) of a formal context (G,M,I)
has the form (A′′, A′) for some subset A⊂G
and the form (B′, B′′) for some subset B ⊂ M.
Conversely, all such pairs are formal concepts.
Compute all formal concepts

37. Observations
• (A′′, A′) ist a formal concept.
• A ⊂ G extent ⇔ A = A′′.
B ⊂ M intent ⇔ B = B′′.
• The intersection of arbitrary many extents is an extent.
The intersection of arbitrary many intents is an intent.

38. Algorithm for Computing all Formal Concepts
A) Determine all Concept Extents
1. Initialize a list of concept extents.
Write for each attribute m ∈ M the extent {m}’ to the list.
2. For any two sets in the list, compute their intersection.
If the result is set that is not yet in the list, then extend the list by this set.
With the extended list, continue to build all pairwise intersections.
Extend the list by the set G.
⇒ The list contains all concept extents.
B) Determine all Concept Intents
3. Compute intents
For every concept extent A in the list compute the corresponding intent A′
to obtain a list of all formal concepts (A, A′).

39. Exercise
Compute the formal concepts of the following formal context.

40. Exercise
1. Initialize a list of concept extents.
Write for each attribute m ∈ M the extent {m}’ to the list.
Item Extent {m}' Attribute m∈M
e1 {Dog, Cat, Carp} {Animal}
e2 {Oak, Potato, Water lily, Reed} {Plant}
e3 {Dog, Cat, Oak, Potato, Reed} {Lives on land}
e4 {Carp, Water lily, Reed} {Lives in water}

41. Exercise
2. For any two sets in the list, compute their intersection.
- If the result is a set that is not yet in the list, then extend the list by this set.
- With the extended list, continue to build all pairwise intersections.
- Extend the list by the set G.
Item Extent Defined by
e1 {Dog, Cat, Carp} {Animal}
e2 {Oak, Potato, Water lily, Reed} {Plant}
e3 {Dog, Cat, Oak, Potato, Reed} {Lives on land}
e4 {Carp, Water lily, Reed} {Lives in water}
e5 ∅ e1 ∩ e2
e6 {Dog, Cat} e1 ∩ e3
e7 {Carp} e1 ∩ e4
e8 {Oak, Potato, Reed} e2 ∩ e3
e9 {Water lily, Reed} e2 ∩ e4
e10 {Reed} e3 ∩ e4
e11 {Dog, Cat, Oak, Potato, Carp, Water lily, Reed} G

42. Exercise
2. For any two sets in the list, compute their intersection.
- If the result is a set that is not yet in the list, then extend the list by this set.
- With the extended list, continue to build all pairwise intersections.
- Extend the list by the set G.
Item Extent Defined by
e1 {Dog, Cat, Carp} {Animal}
e2 {Oak, Potato, Water lily, Reed} {Plant}
e3 {Dog, Cat, Oak, Potato, Reed} {Lives on land}
e4 {Carp, Water lily, Reed} {Lives in water}
e5 ∅ e1 ∩ e2
e6 {Dog, Cat} e1 ∩ e3
e7 {Carp} e1 ∩ e4
e8 {Oak, Potato, Reed} e2 ∩ e3
e9 {Water lily, Reed} e2 ∩ e4
e10 {Reed} e3 ∩ e4
e11 {Dog, Cat, Oak, Potato, Carp, Water lily, Reed} G

43. Exercise
3. Determine intents
For every concept extent A in the list compute the corresponding intent A′
to obtain a list of all formal concepts (A, A′).
Item Extent A Intent A′
e1 {Dog, Cat, Carp} {Animal}
e2 {Oak, Potato, Water lily, Reed} {Plant}
e3 {Dog, Cat, Oak, Potato, Reed} {Lives on land}
e4 {Carp, Water lily, Reed} {Lives in water}
e5 ∅ M
e6 {Dog, Cat} {Animal, lives on land}
e7 {Carp} {Animal, lives in water}
e8 {Oak, Potato, Reed} {Plant, lives on land}
e9 {Water lily, Reed} {Plant, lives in water}
e10 {Reed} {Plant, lives on land, lives in water}
e11 {Dog, Cat, Oak, Potato, Carp, Water lily, Reed} ∅

44. Conceptual Hierarchies
and
Concept Lattices

45. Is there a relation between the formal concepts?
Animal super-concept
Dog, Cat, Carp
≤
Animal, lives on land Animal, lives in water
sub-concept
Dog, Cat Carp
Idea: Order concepts in a sub-concept ̶ super-concept hierarchy

46. Is there a relation between the formal concepts?
Animal super-concept
Dog, Cat, Carp
≤
Animal, lives on land Animal, lives in water
sub-concept
Dog, Cat Carp
The extent of the sub-concept is a subset of the extent of the super-concept
The intent of the super-concept is a subset of the intent of the sub-concept

47. Conceptual Hierarchy
Let (A1, B1) and (A2, B2) be formal concepts of (G,M,I).
(A1, B1) sub-concept of (A2, B2) :⇔ A1 ⊂ A2 [⇔ B2 ⊂ B1 ].
Animal
Dog, Cat, Carp
• (A2, B2) is a super-concept of (A1, B1).
• Notation: (A1, B1) ≤ (A2, B2)
Animal, lives on land
Dog, Cat

48. Conceptual Hierarchy
• The set of all formal concepts of (G, M, I)
is called the concept lattice of the formal context (G, M, I)
and is denoted by B (G,M,I) .

49. Conceptual Hierarchy
Theorem
The concept lattice of a formal context is a partially ordered set.
We need a notion of
neighborhood
⇒ We can draw figures that indicate intricate relationships!!

50. Conceptual Hierarchy
Let P be a set and ≤ is a binary relation on P.
A partially ordered set is a pair (P, ≤), iff
1) x≤x (reflexive)
2) x ≤ y and x ≠ y ⇒ ¬ y ≤ x (antisymmetric)
3) x ≤ y and y ≤ z ⇒ x ≤ z (transitive)
for all x, y, z ∈ P.

51. Conceptual Hierarchy
Let (A1, B1) and (A2, B2) be formal concepts of the context (G,M,I).
(A1, B1) proper sub-concept of (A2, B2) [ (A1, B1) < (A2, B2)]
:⇔ (A1, B1) ≤ (A2, B2) and (A1, B1) ≠ (A2, B2) .
(A2 , B2)
(A1 , B1)

52. Conceptual Hierarchy
Examples: In the following examples (A1, B1) is a proper sub-concept of (A2, B2)
(a) (A2 , B2) (b) (A2 , B2)
(A1 , B1) (A , B )
(A1 , B1)
Question: What is the difference between (a) and (b)?
Answer: In (a) the concept (A1, B1) is the lower neighbor of (A2, B2).
In (b) the concept (A1, B1) is not the lower neighbor of (A2, B2).

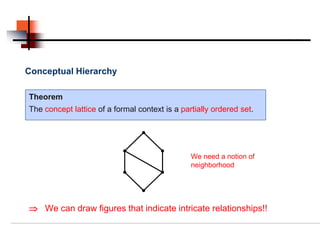
53. Conceptual Hierarchy
Proper sub-concepts can be used to define a notion of neighborhood.
Let (A1, B1) and (A2, B2) be formal concepts of the context (G,M,I) (A2 , B2)
and (A1, B1) is a proper sub-concept of (A2, B2).
(A1, B1) is a lower neighbor of (A2, B2) [(A1, B1)  (A2, B2)], (A , B )
if no formal concept (A, B) exists with
(A1 , B1)
(A1, B1) < (A, B) < (A2, B2).

54. Drawing Concept Lattices
• Draw formal concepts
Draw a small circle for every formal concept.
A circle for a concept is always positioned higher than the circles of its proper sub-concepts.
• Draw lines
Connect each formal concept (circle) with the circles of its lower neighbors.
• Label with attribute names
Attach the attribute m to the circle representing the concept ( {m}′, {m}′′ ).
• Label with object names
Attach each object g to the circle representing the ({g}′′ , {g}′).

55. Exercise
Compute the concept lattice of the following formal concept.

56. Drawing Concept Lattices
G
e11
plant e2 e4 aquatic e1 animal e3 terrestrial
water water
plant
e9 e7 animal e6 land
animal
terrestrial
e8 plants
water lily carp dog, cat oak, potato
plants, on land
e10
& in water
reed
e5
∅

57. Exercise
Compute the formal concepts of the following formal context:
Attributes
Habital zone
Terrestrial
Gas giant
Moon
Earth x x x
Jupiter x x
Objects
Mercury x
Mars x x

58. Exercise
1. Initialize a list of concept extents.
Write for each attribute m ∈ M the extent {m}’ to the list.
Item Extent {m}' Attribute m∈M
e1 {jupiter} {gas giant}
e2 {earth, mercury, mars} {terrestrial}
e3 {earth, jupiter, mars} {moon}
e4 {earth} {habital zone}

59. Exercise
2. For any two sets in the list, compute their intersection.
If the result is a set that is not yet in the list, then extend the list by this set.
With the extended list, continue to build all pairwise intersections.
Extend the list by the set G.
Item Extent Defined by
e1 {jupiter} {gas giant}
e2 {earth, mercury, mars} {terrestrial}
e3 {earth, jupiter, mars} {moon}
e4 {earth} {habital zone}
e5 ∅ e1 ∩ e2
e6 {earth, mars} e2 ∩ e3
e7 {earth, jupiter, mercury, mars} G

60. Exercise
3. Determine intents
For every concept extent A in the list compute the corresponding intent A′
to obtain a list of all formal concepts (A, A′).
Item Extent Intent
e1 {jupiter} {gas giant, moon}
e2 {earth, mercury, mars} {terrestrial}
e3 {earth, jupiter, mars} {moon}
e4 {earth} {terrestrial, moon, habital zone}
e5 ∅ M
e6 {earth, mars} {terrestrial, moon}
e7 {earth, jupiter, mercury, mars} ∅

61. Exercise
G
Concept Lattice e7
terrestrial moon
earth, mercury, e2 e3 earth, jupiter,
mars mars
terrestrial,
e6
moon
earth, mars
gas giant,
terrestrial,
e4 e1 moon
moon, habitual
jupiter
earth
e5
∅

62. Applications

63. Applications
• Web information retrieval
→ How can web search results retrieved by search engines be conceptualized
and represented in a human-oriented form.
• Partner selection for interfirm collaborations
→ Identification of structural similarities between potential partners
according to the characteristics of the prospective partner firms.
• Information systems for IT security management
→ Identification of security-sensitive operations performed by a server.
• Data warehousing and database analysis
→ Controlling the trade of stocks and shares.

64. Bioinformatics
Verducci J S et al. Physiol. Genomics 2006;25:355-363
©2006 by American Physiological Society

65. Bioinformatics
Biclustering / co-clustering
Simultaneous clustering of the
rows and columns of a matrix.
Verducci J S et al. Physiol. Genomics 2006;25:355-363
©2006 by American Physiological Society

66. Summary
• Formal concept analysis provides methods for an automatic derivation
of ontologies from very large collections of objects and their attributes.
• Reveal unknown, hidden and meaningful connections
between groups of objects and groups of attributes.
• The methods are supported by algebra, lattice theory and order theory.
• Visualization techniques are available.
• Strong connections to co-clustering (bi-clustering) methods
(important tools in DNA-microarray analysis).

67. Literature
• Bernhard Ganter, Gerd Stumme, Rudolf Wille (ed.)
Formal Concept Analysis. Foundations and Applications.
Springer, 2005.
• Claudio Carpineto, Giovanni Romano
Concept Data Analysis: Theory and Applications.
Wiley, 2004.
Software
www.fcahome.org.uk/fcasoftware.html

68. Thank you very much!