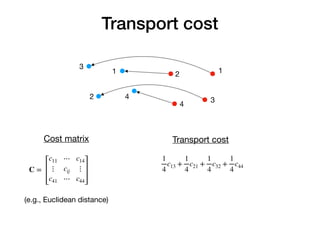
The document discusses the Sinkhorn algorithm for optimal transport. It describes how the Sinkhorn algorithm can be used to find the optimal transport plan between distributions by iteratively applying linear operations. It also introduces the GeomLoss Python library for using Sinkhorn divergences and mentions applications of Sinkhorn for latent permutations and solving jigsaw puzzles.

1. Sinkhorn algorithm and its
applications
PyData Osaka meetup #11
Taku Yoshioka

2. • Problem: Optimal transport
• Algorithm: Sinkhorn algorithm
• Python implementation: GeomLoss
• Another application: latent permutations

3. https://dfdazac.github.io/sinkhorn.html
https://arxiv.org/abs/1802.08665
http://marcocuturi.net/SI.html
https://github.com/jeanfeydy/geomloss

4. • Problem: Optimal transport
• Algorithm: Sinkhorn algorithm
• Python implementation: GeomLoss
• Another application: Jigsaw puzzle

5. Fitting generative models
Observations
Likelihood of generative model
• Fitting generative model using parameter gradient of
likelihood of observations

6. Implicit generative model
• Likelihood not available
• Can generate samples
Low-dimensional
random variable
Deterministic transformation
(e.g., Neural network)
High-dimensional
random variable
Typical example of implicit model

7. Fitting without likelihood function
Observations Samples from generative model
(likelihood not available)
• Fitting generative model without likelihood function (aka
implicit models)
• Alternative to likelihood: distance between these sets of
points (underlying distributions)
• To do this, GAN utilizes classifier (JS-divergence)

8. Distance between distributions
Observations Samples from generative model
(likelihood not available)
i
j
Cost matrix
C =
c11 ⋯ c14
⋮ cij ⋮
c41 ⋯ c44
(e.g., Euclidean distance)

9. Transport cost
11
2
3
4
2
3
4
Transport cost
1
4
c13 +
1
4
c21 +
1
4
c32 +
1
4
c44
Cost matrix
C =
c11 ⋯ c14
⋮ cij ⋮
c41 ⋯ c44
(e.g., Euclidean distance)

10. Transport cost
11
2
3
4
2
3
4
Transport cost
1
4
c11 +
1
4
c23 +
1
4
c34 +
1
4
c42
Minimum transport cost over possible assignment
-> Optimal transport (discrete case)
Cost matrix
C =
c11 ⋯ c14
⋮ cij ⋮
c41 ⋯ c44
(e.g., Euclidean distance)

11. Generalization of assignment
11
2
3
4
2
3
4
Coupling matrix
P =
p11 ⋯ p14
⋮ pij ⋮
p41 ⋯ p44
Transport cost
⟨C, P⟩ ≡
∑
ij
CijPij
Cost matrix
C =
c11 ⋯ c14
⋮ cij ⋮
c41 ⋯ c44
p13c13
c42p42
∑
j
pij =
1
4
,
∑
i
pij =
1
4 P1 = r, PT
1 = cGeneral form:
p21c21

12. • Problem: Optimal transport
• Algorithm: Sinkhorn algorithm
• Python implementation: GeomLoss
• Another application: Jigsaw puzzle

13. Regularized OT problem
d = min
P
⟨C, P⟩,
d = min
P
⟨C, P⟩ − ϵH(P)
Optimal transport
Entropy regularized
P1 = r, PT
1 = c

14. Regularized OT problem
d = min
P
⟨C, P⟩,
d = min
P
⟨C, P⟩ − ϵH(P)
Optimal transport
Entropy regularized
Solution obtained with Lagrangian (Cuturi 2013, Lemma 2)
P = diag(u) ⋅ K ⋅ diag(v) Kij = exp(−cij/ϵ), u ≥ 0, v ≥ 0
The same form of the solution obtained with
Sinkhorn algorithm
P1 = r, PT
1 = c

15. Sinkhorn algorithm
u(k+1)
=
r
Kv(k)
v(k+1)
=
c
KTu(k+1)
pij = diag(u) ⋅ K ⋅ diag(v) Kij = exp(−cij/ϵ), u ≥ 0, v ≥ 0
How to get u and v: repeat applying linear operations until
convergence (stops at a finite iteration in practice)
Sinkhorn and Knopp (1967) proposed this iterative
algorithm and analyzed convergence.

16. Sinkhorn algorithm
u(k+1)
=
r
Kv(k)
v(k+1)
=
c
KTu(k+1)
P = diag(u) ⋅ K ⋅ diag(v) Kij = exp(−cij/ϵ), u ≥ 0, v ≥ 0
Backprop
How to get u and v: repeat applying linear operations until
convergence (stops at a finite iteration in practice)
https://arxiv.org/abs/1706.00292

17. • Problem: Optimal transport
• Algorithm: Sinkhorn algorithm
• Python implementation: GeomLoss
• Another application: Jigsaw puzzle

18. GeomLoss library (pytorch)
https://github.com/jeanfeydy/geomloss
• Provides the following loss functions:
• Kernel norms (maximum mean discrepancies)
• Hausdorff divergences
• Unbiased Sinkhorn divergences
• Can be used in a wide variety of settings, from shape
analysis (LDDMM, optimal transport…) to machine
learning (kernel methods, GANs…) and image processing.

19. https://www.kernel-operations.io/geomloss/_auto_examples/comparisons/plot_gradient_flows_2D.html#sphx-glr-auto-examples-
comparisons-plot-gradient-flows-2d-py

21. • Problem: Optimal transport
• Algorithm: Sinkhorn algorithm
• Python implementation: GeomLoss
• Another application: Jigsaw puzzle

22. Latent permutations
https://duvenaud.github.io/learn-discrete/slides/Gumbel-Sinkhorn-Slides.pdf

23. Jigsaw puzzle

24. Jigsaw puzzle

26. Summary
• Optimal transport for measuring distance of distributions
• Sinkhorn algorithm is just a sequential application of
linear operation, thus it’s possible to backprop
• GeomLoss makes it easy to use Sinkhorn algorithm with
PyTorch
• Sinkhorn algorithm can be used to find a good latent
permutation from observation