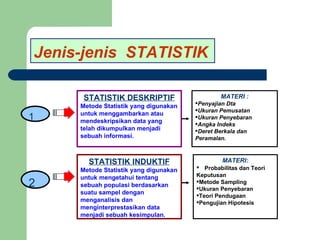
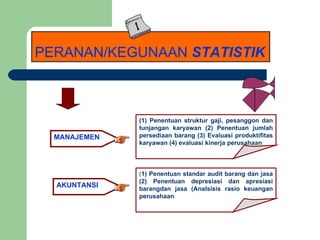
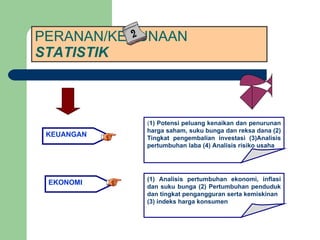
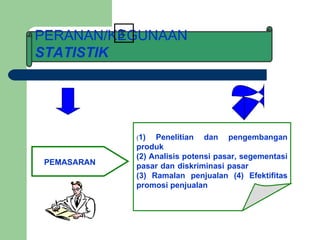
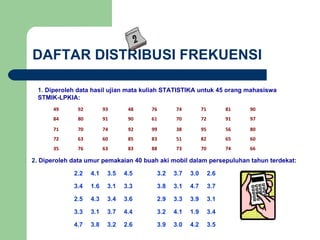
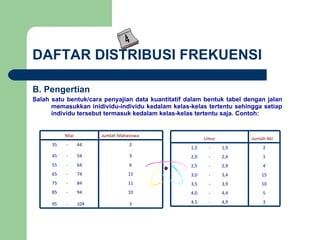
Dokumen tersebut memberikan penjelasan mengenai statistika dan distribusi frekuensi. Secara singkat, statistika digunakan untuk menganalisis data kuantitatif dengan merangkumnya ke dalam tabel atau grafik, sedangkan distribusi frekuensi merupakan salah satu cara penyajian data statistik dengan memasukkan data ke dalam kelas-kelas tertentu beserta frekuensinya.

1. STATISTIKA Untuk Ekonomi (untuk lingkungan sendiri STIE Muhammadiyah Bandung) Oleh: Ia Kurnia, Drs., M.Pd

2. Definisi STATISTIK Sebagai keterangan 2 yang dibutuhkan oleh negara dan berguna bagi negara. Sebagai data kuantitatif baik yang masih belum teersusun maupun yang telah tersusun dalam bentuk tabel (kumpulan data yang berwujud angka-angka). Sebagai metode statistik dan bukan kumpulan data kuantitatif ( Wilks, Elementary Statistical Analysis , 1949: bab 2). Metode guna mengumpulkan, mengolah, menyajikan, menganalisa dan menginterpretasi data yang berwujud angka-angka sehingga angka tersebut berbicara ( Croxton & Cowden, Applied General Statistics , 1955: bab 1 ). Definisi STATISTIK

3. Definisi STATISTIK SUDJANA ( Statistika Untuk Ekonomi Dan Niaga , 1996); RIDUWAN ( Dasar-dasar Statistika, 2003); SUHARYADI, Dkk. ( Statistika Untuk Ekonomi & Keuangan Modern , 2003) STATISTIK : Kumpulan angka-angka yang menggambarkan sesuatu persoalan, dimana angka-angka tersebut disusun dalam tabel, daftar, diagram ataupun grafik disertai keterangan. STATISTIKA : Pengetahuan yang berhubungan dengan cara pengumpulan bahan/keterangan, pengolahan serta penganalisaannya, penarikan kesimpulan serta pembuatan keputusan yang beralasan berdasarkan penganalisaan J. SUPRANTO ( Statistik, Teori dan Aplikasi, 2000) : Statistik dalam pengertian sempit : pengertian STATISTIK (dalam Sudjana dan Riduwan). (2) Statistik dalam pengertian luas : pengertian Statistika (dalam Sudjana dan Riduwan). Definisi STATISTIK

4. Definisi STATISTIK Sedangkan ANTO DAJAN ( Pengantar Metode Statistik, 1986) tidak membedakan Statistik dan Statistika, maka ketika berbicara Statistik seharusnya mengenai Metode Statistik . Statistics is the science and art of the development and application of the most effective methods of collecting, tabulating, and interpreting quantitative data in such a manner that the fallibility of conclusions and estimates may be assessed by means of inductive reasoning based on the mathematics of probability. ( Anderson and Bancroft , Statistical Theory and Research, 1952. Definisi STATISTIK 3

5. Jenis-jenis STATISTIK 1 STATISTIK DESKRIPTIF Metode Statistik yang digunakan untuk menggambarkan atau mendeskripsikan data yang telah dikumpulkan menjadi sebuah informasi. MATERI : Penyajian Dta Ukuran Pemusatan Ukuran Penyebaran Angka Indeks Deret Berkala dan Peramalan. 2 STATISTIK INDUKTIF Metode Statistik yang digunakan untuk mengetahui tentang sebuah populasi berdasarkan suatu sampel dengan menganalisis dan menginterprestasikan data menjadi sebuah kesimpulan. MATERI: Probabilitas dan Teori Keputusan Metode Sampling Ukuran Penyebaran Teori Pendugaan Pengujian Hipotesis

6. PERANAN/KEGUNAAN STATISTIK MANAJEMEN (1) Penentuan struktur gaji, pesanggon dan tunjangan karyawan (2) Penentuan jumlah persediaan barang (3) Evaluasi produktifitas karyawan (4) evaluasi kinerja perusahaan AKUNTANSI ( 1) Penentuan standar audit barang dan jasa (2) Penentuan depresiasi dan apresiasi barangdan jasa (Analsisis rasio keuangan perusahaan

7. PERANAN/KEGUNAAN STATISTIK KEUANGAN ( 1) Potensi peluang kenaikan dan penurunan harga saham, suku bunga dan reksa dana (2) Tingkat pengembalian investasi (3)Analisis pertumbuhan laba (4) Analisis risiko usaha EKONOMI (1) Analisis pertumbuhan ekonomi, inflasi dan suku bunga (2) Pertumbuhan penduduk dan tingkat pengangguran serta kemiskinan (3) indeks harga konsumen

8. PERANAN/KEGUNAAN STATISTIK PEMASARAN ( 1) Penelitian dan pengembangan produk (2) Analisis potensi pasar, segementasi pasar dan diskriminasi pasar (3) Ramalan penjualan (4) Efektifitas promosi penjualan 3

9. KEGUNAAN STATISTIKA sebagai ALAT KOMUNIKASI DESKRIPSI REGRESI KORELASI KOMPARASI

10. LANDASAN LANDASAN KERJA STATISTIKA VARIASI REDUKSI GENERALISASI

11. D A T A MENURUT SIFATNYA MENURUT SUMBERNYA MENURUT PROSES PENGOLAHANNYA

12. DAFTAR DISTRIBUSI FREKUENSI Tujuan Instruksional Khusus: Setelah mengikuti materi ini, mahasiswa diharapkan mampu: Menjelaskan pengertian distribusi frekuensi Menyebutkan tujuan distribusi frekuensi Menyusun distribusi frekuensi Membedakan jenis-jenis distribusi frekuensi Mengggambarkan Grafik Distribusi Frekuensi : (a) Histogram (b) Polygon Frekuensi © Kurva Ogive Membedakan model-model populasi berdasarkan grafik distribusi frekuensi

13. DAFTAR DISTRIBUSI FREKUENSI A. Tujuan Guna memperoleh gambaran yang sederhana, jelas dan sistematis mengenai peristiwa-peristiwa yang dinyatakan dalam angka. Perhatikan dua contoh berikut ini:

14. DAFTAR DISTRIBUSI FREKUENSI 2. Diperoleh data umur pemakaian 40 buah aki mobil dalam persepuluhan tahun terdekat: 1. Diperoleh data hasil ujian mata kuliah STATISTIKA untuk 45 orang mahasiswa STMIK-LPKIA: 2.2 4.1 3.5 4.5 3.2 3.7 3.0 2.6 3.4 1.6 3.1 3.3 3.8 3.1 4.7 3.7 2.5 4.3 3.4 3.6 2.9 3.3 3.9 3.1 3.3 3.1 3.7 4.4 3.2 4.1 1.9 3.4 4.7 3.8 3.2 2.6 3.9 3.0 4.2 3.5 49 92 93 48 76 74 71 81 90 84 80 91 90 61 70 72 91 97 71 70 74 92 99 38 95 56 80 72 63 60 85 83 51 82 65 60 35 76 63 83 88 73 70 74 66

15. DAFTAR DISTRIBUSI FREKUENSI Dari data kasar di atas, secara langsung tidak begitu besar kegunaannya bagi penggambaran peristiwa-peristiwa yang bersifat kuantitatif. Beberapa pertanyaan yang sulit secara langsung bisa dijawab: Berapa mahasiswa yang memperoleh nilai antara 85 dan 94 ? Berapa angka nilai yang diperoleh oleh sebagian besar mahasiswa ? Berapa persen mahasiswa yang memperoleh nilai dibawah 50 ? Berapa mahasiswa yang memperoleh nilai diatas rata-ratan ? Berapa % aki yang umur pakainya diatas 3 tahun ? Jika jaminan pemakaian aki tersebut selama 4 tahun, akankah kita membeli aki tersebut ? Lebih sulit lagi apabila data kasar di atas terdiri dari beribu-ribu angka. Keterangan-keterangan akan lebih banyak diperoleh jika data kasar di atas disusun secara berkelompok dalam sebuah daftar yang disebut DAFTAR DISTRIBUSI FREKUENSI .

16. DAFTAR DISTRIBUSI FREKUENSI B. Pengertian Salah satu bentuk/cara penyajian data kuantitatif dalam bentuk tabel dengan jalan memasukkan inidividu-individu kedalam kelas-kelas tertentu sehingga setiap individu tersebut termasuk kedalam kelas-kelas tertentu saja. Contoh: Nilai Jumlah Mahasiswa 35 - 44 2 45 - 54 3 55 - 64 6 65 - 74 15 75 - 84 11 85 - 94 10 95 - 104 3 Umur Jumlah Aki 1,5 - 1,9 2 2,0 - 2,4 1 2,5 - 2,9 4 3,0 - 3,4 15 3,5 - 3,9 10 4,0 - 4,4 5 4,5 - 4,9 3

17. DAFTAR DISTRIBUSI FREKUENSI Istilah-istilah dalam Distribusi Frekuensi Frekuensi : Banyaknya individu yang terdapat pada kelas interval Class/Kelas : Penggolongan data yang dibatasi dengan nilai terendah dan nilai tertinggi Class Limit/Batas Kelas : Nilai batas dari tiap kelas yang dibagi atas: 1. Stated Class Limit : Nilai-nilai yang tertera di dalam suatu distribusi frekuensi, terdiri dari: 1.1 Lower Class Limit yaitu batas bawah kelas 1.2 Upper Class Limit yaitu batas atas kelas 2. Class Boundaries/True Limits : nilai yang membatasi antara tiap dua kelas yang berurutan, digunakan untuk menggambarkan grafik suatu distribusi frekuensi, terdiri dari: 2.1 Lower Class Boundary : Batas Bawah Kelas yang sebenarnya 2.2 Upper Class Boundary : Batas atas kelas yang sebenarnya Class Interval/Panjang Kelas/Lebar Kelas : Merupakan lebar dari sebuah kelas dan dihitung dari perbedaan Class Boundaries atau perbedaan dari dua titik tengah kelas yang berurutan. Mid Point/Class Mark : bilangan yang tepat berada ditengah antara Lower Class Limit dan Upper Class Limit.

18. DAFTAR DISTRIBUSI FREKUENSI D. Tahap Penyusunan Distribusi Frekuensi 1. Meng- array data kasar menurut urutan besar-kecil Bisa tidak dilaksanakan tergantung banyak-sedikitnya data Untuk mempermudah perhitungan frekuensi 2. Menentukan jumlah kelas Tergantung kepada pertimbangan praktis pengolah data Berhubungan erat dengan Interval Kelas, sifat data kasar dan jumlah angka Umumnya jumlah kelas berkisar 5 - 15 kelas Untuk kondisi tertentu, bisa menggunakan rumus STURGES (1926): k = jumlah kelas n = jumlah data 3. Menentukan besaran RANGE (jarak sebaran data) Dapat menggunakan: data terbesar dikurangi data terkecil Atau perbedaan data terkecil yang telah mengalami pembulatan kebawah dan data terbesar yang telah mengalami pembulatan keatas k = 1 + 3,3 log n

19. DAFTAR DISTRIBUSI FREKUENSI 4. Mencari Interval/Panjang/Lebar Kelas R = Range k = Jumlah Kelas Umumnya, hasil dibulatkan ke atas. 5. Menentukan Batas Bawah Kelas Pertama Bisa menggunakan data terkecil atau data yang lebih kecil dari data terkecil yang dianggap paling praktis perhitungannya Batas bawah kelas berikutnya = Batas Bawah + CI 6. Tentukan frekuensi bagi masing-masing kelas, jumlah frekuensi tersebut harus sama dengan jumlah data. 7

20. DAFTAR DISTRIBUSI FREKUENSI E. Jenis Distribusi Frekuensi Absolut Relatif Absolut Kumulatif “Kurang Dari” Absolut Kumulatif “Atau Lebih” Relatif Kumulatif “Kurang Dari” Relatif Kumulatif “Atau lebih”