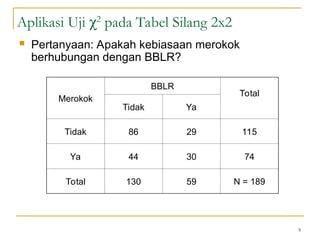
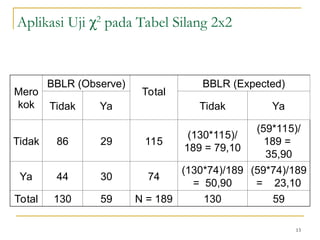
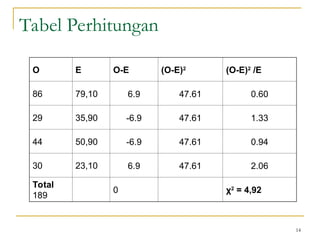
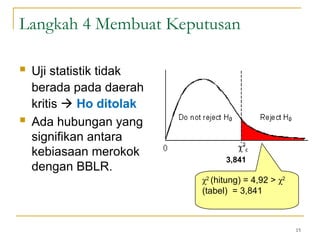
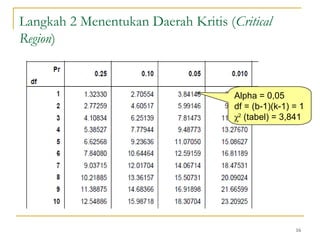
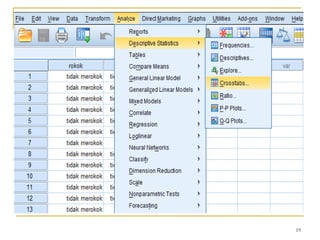
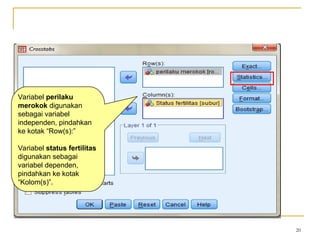
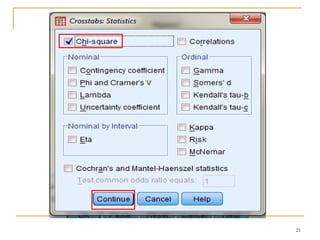
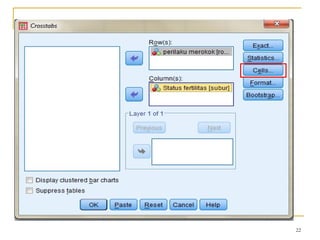
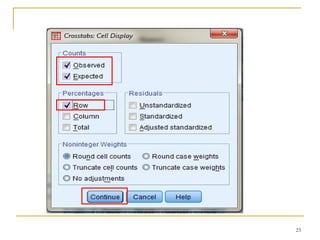
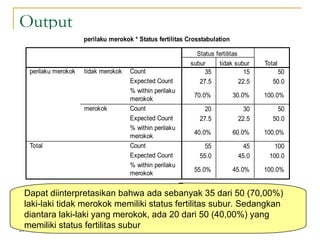
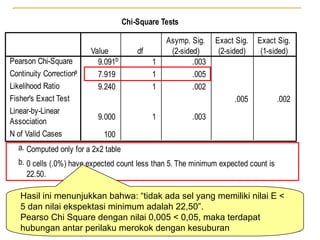
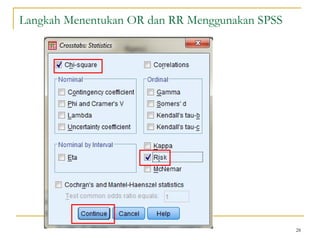
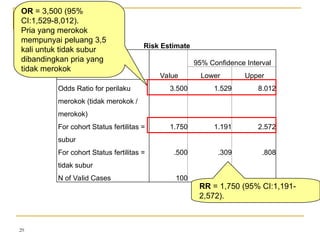
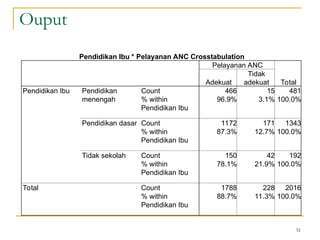
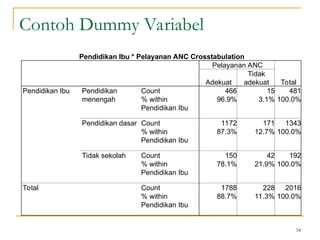
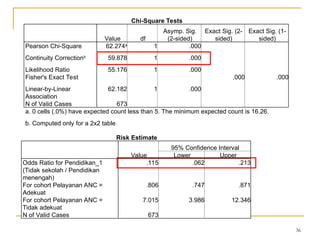
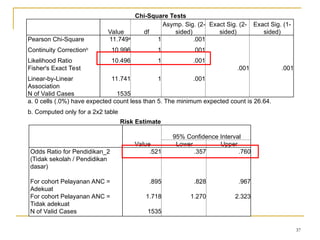
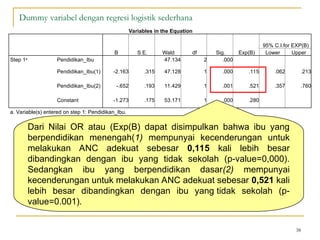
Dokumen ini membahas penggunaan SPSS dalam analisis statistik deskriptif, mencakup metode seperti frekuensi, uji chi-square, dan analisis hubungan antar variabel. Selain itu, dokumen menjelaskan aplikasi chi-square pada berbagai tabel serta cara menghitung odds ratio dan relative risk. Terakhir, terdapat contoh penerapan analisis pada hubungan antara perilaku merokok dan status fertilitas pria, serta pendidikan ibu terhadap pemanfaatan pelayanan antenatal care.

1. Abdul Aziz Setiawan
STF Muhammadiyah Tangerang
2020
SPSS
(Statistical Product and Service Solutions)
Deskriptif

2. Bagian SPSS yang berhubungan dengan
Statistik Deskriptif
1. Frequencies
Membahas beberapa penjabaran ukuran statistik deskriptif seperti Mean,
Median, Kuartil, Persentil, Standar Deviasi dll
2. Descriptive
Berfungsi untuk mengetahui skor z dari suatu distribusi data dan menguji
apakah data berdistribusi normal atau tidak
3. Explore
Berfungsi untuk memeriksa lebih teliti terhadap sekelompok data dengan
Box-Plot dan Steam and Leaf Plot, selain beberapa uji tambahan untuk
menguji apakah data berasal dari distribusi normal.

3. 4. Crosstab
Digunakan untuk menyajikan deskripsi data dalam bentuk
tabel silang. Menu ini juga dilengkapi dengan analisis
hubungan di antara baris dan kolom, seperti independensi
antara mereka, besar hubungannya dsb
5. Case Summaries
Digunakan untuk melihat lebih jauh isi statistik deskriptif yang
meliputi subgroup dari sebuah kasus.
Bagian SPSS yang berhubungan dengan
Statistik Deskriptif

4. Uji Statistik yang Digunakan
Untuk ANALISA BIVARIAT
Variabel I Variabel II J enis uji statistik yang
digunakan
Katagorik  Katagorik - Kai kuadrat
- Fisher Exact
Katagorik  Numerik - Uji T
- ANOVA
Numerik  Numerik - Korelasi
- Regresi
4

5.  Apakah ada perbedaan proporsi
hipertensi pada populasi perokok dan
populasi bukan perokok
 Apakah ada perbedaan proporsi
anemia pada ibu dengan sosek
ekonomi tinggi, sedang, dan rendah
 Disusun dalam suatu tabel (tabel
kontingensi)
5
Contoh

6.  Secara spesifik uji chi square dapat
digunakan untuk menentukan/menguji:
◦ Ada tidaknya hubungan/asosiasi antara 2
variabel (test of independency)
◦ Apakah suatu kelompok homogen dengan
sub kelompok lain (test of homogenity)
◦ Apakah ada kesesuaian antara
pengamatan dengan parameter tertentu
yang dispesifikasikan (Goodness of fit)
6
TUJUAN UJI CHI SQUARE

7.  Jenis data kategori
 Sampel independen
 Distribusi tidak normal/tidak
diketahui distribusinya (free
distribution)
7
PERSYARATAN/ASUMSI

8.  Membandingkan frekuensi yang terjadi (observasi)
dengan frekuensi harapan (ekspektasi)
 Pembuktian dengan uji chi square menggunakan
formula:
Pearson Chi Square:
8
PRINSIP DASAR UJI CHI SQUARE
dengan df = (b-1)(k-1)
fo= nilai observasi (pengamatan)
fe = nilai ekspektasi (harapan)
b = jumlah baris
k = jumlah kolom


E
E
O 2
)
(
χ2
=

9. Aplikasi Uji χ2
pada Tabel Silang 2x2
 Pertanyaan: Apakah kebiasaan merokok
berhubungan dengan BBLR?
9
Merokok
BBLR
Total
Tidak Ya
Tidak 86 29 115
Ya 44 30 74
Total 130 59 N = 189

10.  Hipotesis nol (Ho):
 Proporsi BBLR pada ibu perokok sama dengan
proporsi BBLR pada ibu yang bukan perokok
 ATAU tidak ada hubungan merokok dengan kejadian
BBLR
 Hipotesis alternatif (Ha):
 Proporsi BBLR pada ibu perokok berbeda proporsi
BBLR pada ibu yang bukan perokok
 ATAU ada hubungan merokok dengan kejadian BBLR
10
Langkah 1 Menentukan hipotesis statistik

11. Langkah 3 Perhitungan Uji Statistik
 Formula:
χ2
=
Metode:
1. Hitung nilai/frekuensi ekspektasi dari masing-masing sel.
2. Lengkapi tabel perhitungan untuk memperoleh χ2
(hitung)


E
E
O 2
)
(
11

12. Menghitung nilai/frekuensi ekspektasi
masing-masing sel
 E =
 Perkalian antara marginal kolom dan marginal
baris masing-masing sel dan dibagi N.
 (130*115)/189 = 79,10
 (59*115)/189 = 35,90
 (130*74)/189 = 50,90
 (59*74)/189 = 23,10
N
kolom
marginal
baris
marginal 
12

13. Aplikasi Uji χ2
pada Tabel Silang 2x2
13
Mero
kok
BBLR (Observe)
Total
BBLR (Expected)
Tidak Ya Tidak Ya
Tidak 86 29 115
(130*115)/
189 = 79,10
(59*115)/
189 =
35,90
Ya 44 30 74
(130*74)/189
= 50,90
(59*74)/189
= 23,10
Total 130 59 N = 189 130 59

14. Tabel Perhitungan
O E O-E (O-E)2
(O-E)2
/E
86 79,10 6.9 47.61 0.60
29 35,90 -6.9 47.61 1.33
44 50,90 -6.9 47.61 0.94
30 23,10 6.9 47.61 2.06
Total
189
0 χ2
= 4,92
14

15.  Uji statistik tidak
berada pada daerah
kritis  Ho ditolak
 Ada hubungan yang
signifikan antara
kebiasaan merokok
dengan BBLR.
15
Langkah 4 Membuat Keputusan
χ2
(hitung) = 4,92 > χ2
(tabel) = 3,841
3,841

16. 16
Langkah 2 Menentukan Daerah Kritis (Critical
Region)
Alpha = 0,05
df = (b-1)(k-1) = 1
χ2
(tabel) = 3,841

17.  Pearson Chi Square/Likehood
Untuk tabel > 2x2 (misal 3x2 atau 3x3) dengan memperhatikan
persyaratan:
◦ Tidak ada frekuensi harapan kurang dari 1 (E<1)
◦ Nilai frekuensi harapan < 5 maksimal 20%
◦ Apabila kedua persyaratan di atas tidak dipenuhi, maka
penggabungan kategori perlu dilakukan agar diperoleh nilai
harapan yang berharga besar
 Yates Correction:
Untuk tabel 2x2 bila tidak ada nilai E < 5, maka dipakai
Continuity Correction
 Fisher Exact Test
Untuk tabel 2x2 bila terdapat nilai E < 5 maka digunakan Uji
Fisher Exact
17
Persyaratan Penggunaan Chi Square

18.  Kasus
Suatu penelitian ingin mengetahui hubungan
antara perilaku merokok (merokok dan tidak
merokok) dengan status fertilitas seorang pria
(subur dan tidak subur).
18
Aplikasi Uji Chi Square (Tabel 2x2)
Menggunakan Spss

19. 19

20. 20
Variabel perilaku
merokok digunakan
sebagai variabel
independen, pindahkan
ke kotak “Row(s):”
Variabel status fertilitas
digunakan sebagai
variabel dependen,
pindahkan ke kotak
“Kolom(s)”.

21. 21

22. 22

23. 23

24. 24
Output
perilaku merokok * Status fertilitas Crosstabulation
35 15 50
27.5 22.5 50.0
70.0% 30.0% 100.0%
20 30 50
27.5 22.5 50.0
40.0% 60.0% 100.0%
55 45 100
55.0 45.0 100.0
55.0% 45.0% 100.0%
Count
Expected Count
% within perilaku
merokok
Count
Expected Count
% within perilaku
merokok
Count
Expected Count
% within perilaku
merokok
tidak merokok
merokok
perilaku merokok
Total
subur tidak subur
Status fertilitas
Total
Dapat diinterpretasikan bahwa ada sebanyak 35 dari 50 (70,00%)
laki-laki tidak merokok memiliki status fertilitas subur. Sedangkan
diantara laki-laki yang merokok, ada 20 dari 50 (40,00%) yang
memiliki status fertilitas subur

25. 25
Chi-Square Tests
9.091b 1 .003
7.919 1 .005
9.240 1 .002
.005 .002
9.000 1 .003
100
Pearson Chi-Square
Continuity Correctiona
Likelihood Ratio
Fisher's Exact Test
Linear-by-Linear
Association
N of Valid Cases
Value df
Asymp. Sig.
(2-sided)
Exact Sig.
(2-sided)
Exact Sig.
(1-sided)
Computed only for a 2x2 table
a.
0 cells (.0%) have expected count less than 5. The minimum expected count is
22.50.
b.
Hasil ini menunjukkan bahwa: “tidak ada sel yang memiliki nilai E <
5 dan nilai ekspektasi minimum adalah 22,50”.
Pearso Chi Square dengan nilai 0,005 < 0,05, maka terdapat
hubungan antar perilaku merokok dengan kesuburan

26.  Uji chi quare hanya membuktikan bahwa ada
hubungan (P-value)
 Tidak menggambarkan kekuatan hubungan.
 Untuk menggambarkan hubungan digunakan
ukuran OR dan RR
26
Keterbatasan Uji Chi Square

27.  RR (Relative Risk) =
 OR (Odds Ratio) = AD / BC
27
Kekuatan Hubungan
A/(A+B)
---------
C/(C+D)

28. 28
Langkah Menentukan OR dan RR Menggunakan SPSS

29. 29
Output
Risk Estimate
Value
95% Confidence Interval
Lower Upper
Odds Ratio for perilaku
merokok (tidak merokok /
merokok)
3.500 1.529 8.012
For cohort Status fertilitas =
subur
1.750 1.191 2.572
For cohort Status fertilitas =
tidak subur
.500 .309 .808
N of Valid Cases 100
OR = 3,500 (95%
CI:1,529-8,012).
Pria yang merokok
mempunyai peluang 3,5
kali untuk tidak subur
dibandingkan pria yang
tidak merokok
RR = 1,750 (95% CI:1,191-
2,572).

30.  Contoh:
Ingin diketahui apakah ada hubungan antara
tingkat pendidikan ibu dengan pemanfaatan
pelayanan ANC
30
Aplikasi Uji Chi Square pada Tabel > 2x2

31. 31
Ouput
Pendidikan Ibu * Pelayanan ANC Crosstabulation
Pelayanan ANC
Total
Adekuat
Tidak
adekuat
Pendidikan Ibu Pendidikan
menengah
Count 466 15 481
% within
Pendidikan Ibu
96.9% 3.1% 100.0%
Pendidikan dasar Count 1172 171 1343
% within
Pendidikan Ibu
87.3% 12.7% 100.0%
Tidak sekolah Count 150 42 192
% within
Pendidikan Ibu
78.1% 21.9% 100.0%
Total Count 1788 228 2016
% within
Pendidikan Ibu
88.7% 11.3% 100.0%

32. Chi-Square Tests
Value df
Asymp. Sig. (2-
sided)
Pearson Chi-Square 56.253a
2 .000
Likelihood Ratio 63.661 2 .000
Linear-by-Linear Association 56.204 1 .000
N of Valid Cases 2016
a. 0 cells (.0%) have expected count less than 5. The minimum expected count is
21.71.
32
Output Ho ditolak atau ada
hubungan “pendidikan ibu”
dengan “anc”.

33.  Pada tabel > 2 x 2, tidak bisa ditampilkan
nilai OR
 Tiga cara:
 Harus dibuat dummy variabel tabel dahulu,
kemudian dilakukan Crosstabs
 Lakukan analisis regresi logistik sederhana
33
Dummy Variabel

34. 34
Contoh Dummy Variabel
Pendidikan Ibu * Pelayanan ANC Crosstabulation
Pelayanan ANC
Total
Adekuat
Tidak
adekuat
Pendidikan Ibu Pendidikan
menengah
Count 466 15 481
% within
Pendidikan Ibu
96.9% 3.1% 100.0%
Pendidikan dasar Count 1172 171 1343
% within
Pendidikan Ibu
87.3% 12.7% 100.0%
Tidak sekolah Count 150 42 192
% within
Pendidikan Ibu
78.1% 21.9% 100.0%
Total Count 1788 228 2016
% within
Pendidikan Ibu
88.7% 11.3% 100.0%

35.  Untuk membuat dummy variabel dari pendidikan
(0.Pendidikan menengah, 1. Pendidikan dasar & 2.
Tidak sekolah), ditetapkan kelompok mana yang akan
dijadikan sebagai pembanding
 Sebagai kelompok pembanding kita tetapkan Tidak
sekolah.
 Melakukan transformasi data dengan menu RECODE:
 Pendidikan_1 (0=Tidak sekolah, 1=Pendidikan menengah)
 Pendidikan_2 (0=Tidak sekolah, 1=Pendidikan dasar)
35

36. Risk Estimate
Value
95% Confidence Interval
Lower Upper
Odds Ratio for Pendidikan_1
(Tidak sekolah / Pendidikan
menengah)
.115 .062 .213
For cohort Pelayanan ANC =
Adekuat
.806 .747 .871
For cohort Pelayanan ANC =
Tidak adekuat
7.015 3.986 12.346
N of Valid Cases 673
Chi-Square Tests
Value df
Asymp. Sig.
(2-sided)
Exact Sig. (2-
sided)
Exact Sig. (1-
sided)
Pearson Chi-Square 62.274a
1 .000
Continuity Correctionb
59.878 1 .000
Likelihood Ratio 55.176 1 .000
Fisher's Exact Test .000 .000
Linear-by-Linear
Association
62.182 1 .000
N of Valid Cases 673
a. 0 cells (.0%) have expected count less than 5. The minimum expected count is 16.26.
b. Computed only for a 2x2 table
36

37. Chi-Square Tests
Value df
Asymp. Sig. (2-
sided)
Exact Sig. (2-
sided)
Exact Sig. (1-
sided)
Pearson Chi-Square 11.749a
1 .001
Continuity Correctionb
10.996 1 .001
Likelihood Ratio 10.496 1 .001
Fisher's Exact Test .001 .001
Linear-by-Linear
Association
11.741 1 .001
N of Valid Cases 1535
a. 0 cells (.0%) have expected count less than 5. The minimum expected count is 26.64.
b. Computed only for a 2x2 table
Risk Estimate
Value
95% Confidence Interval
Lower Upper
Odds Ratio for Pendidikan_2
(Tidak sekolah / Pendidikan
dasar)
.521 .357 .760
For cohort Pelayanan ANC =
Adekuat
.895 .828 .967
For cohort Pelayanan ANC =
Tidak adekuat
1.718 1.270 2.323
N of Valid Cases 1535
37

38. Variables in the Equation
B S.E. Wald df Sig. Exp(B)
95% C.I.for EXP(B)
Lower Upper
Step 1a
Pendidikan_Ibu 47.134 2 .000
Pendidikan_Ibu(1) -2.163 .315 47.128 1 .000 .115 .062 .213
Pendidikan_Ibu(2) -.652 .193 11.429 1 .001 .521 .357 .760
Constant -1.273 .175 53.171 1 .000 .280
a. Variable(s) entered on step 1: Pendidikan_Ibu.
Dari Nilai OR atau (Exp(B) dapat disimpulkan bahwa ibu yang
berpendidikan menengah(1) mempunyai kecenderungan untuk
melakukan ANC adekuat sebesar 0,115 kali lebih besar
dibandingkan dengan ibu yang tidak sekolah (p-value=0,000).
Sedangkan ibu yang berpendidikan dasar(2) mempunyai
kecenderungan untuk melakukan ANC adekuat sebesar 0,521 kali
lebih besar dibandingkan dengan ibu yang tidak sekolah (p-
value=0.001).
38
Dummy variabel dengan regresi logistik sederhana