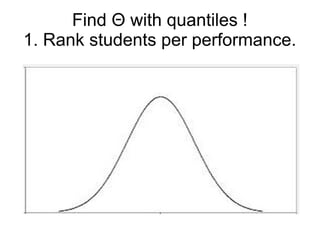
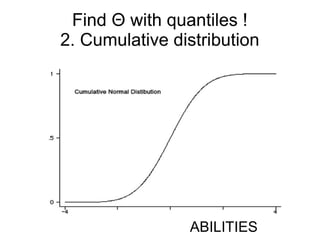
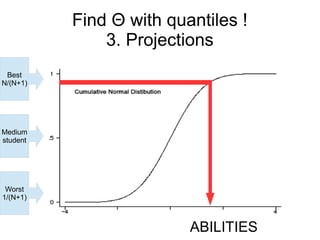
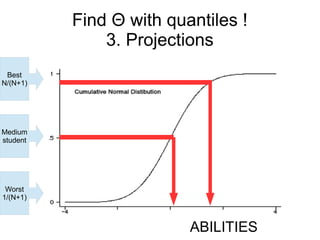
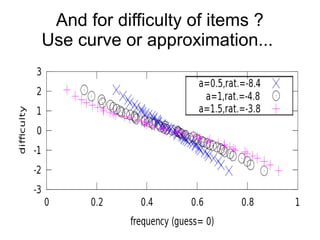
This document provides an overview of statistical concepts related to item response theory (IRT), including posterior probability, Bayes' theorem, maximum a posteriori (MAP) estimation, and the Jacobi algorithm. It discusses how to initialize IRT parameters like student abilities and item parameters, and evaluates options for fitting IRT models like R and Octave packages.

1. A little bit of statistics
P( waow | news ) = ?

2. Posterior probability
● In case of independent items,
● P( Observations | Θ) = product of
P( Observation1 | Θ)
x P( Observation2 | Θ)
x …
x P( ObservationZ | Θ)

3. Bayes theorem
● Bayes :
P( Θ | observations) P(observations)
= P( observations | Θ) P(Θ)
● So :
P( Θ | observations) = P(observations | Θ)
x P(Θ) / P(observation)

4. So, by independ. Items + Bayes,
● P( Θ | observations ) is proportional to
P(Θ) x P( obs1 | Θ) x … x P(obsZ | Θ)
● Definitions :
– MAP (maximum a posteriori) : find Θ* such that
P(Θ*|observations) is max
– BPE (Bayesian posterior expectation): find ΘE =
expectation of (Θ|observations)
– Maximum likelihood : P(Θ) uniform
– there are other possible tools
– ErrorEstimate = Expect. (Θ – estimator)2

5. log-likelihood
● Instead of probas, use log-probas.
● Because :
– Products become sums ==> more precise on a
computer for very small probabilities

6. Finding the MAP (or others
estimates)
● Dimension 1 :
– Golden Search (unimodal)
– Grid Search (multimodal, slow)
– Robust search (compromise)
– Newton Raphson (unimodal, precise expensive
computations)
● Dimension large :
– Jacobi algorithm
– Or Gauss-Seidel, or Newton, or NewUoa, or ...

7. Jacobi algorithm for maximizing in
dimension D>1
● x=clever initialization, if possible
● While ( ||x' – x|| > epsilon )
– x'=current x
– For each parameter x(i), optimize it
● by a 1Dim algorithm
● with just a few iterates
Jacobi = great when the objective function
– can be restricted to 1 parameter
– and then be much faster

8. Jacobi algorithm for maximizing in
dimension D>1
● x=clever initialization, if possible
● While ( ||x' – x|| > epsilon )
– x'=current x
– For each parameter x(i), optimize it
● One iteration of robust search
● But don't decrease the interval if optimum = close to current bounds
Jacobi = great when the objective function
– can be restricted to 1 parameter
– and then be much faster

9. Possible use
● Computing student's abilities, given item
parameters
● Computing item parameters, given student
abilities
● Computing both item parameters and student
abilities (need plenty of data)

10. Priors
● How to know P(Θ) ?
● Keep in mind that difficulties and abilities are
translation invariant
– ==> so you need a reference
– ==> possibly reference = average Θ = 0
● If you have a big database and trust your model
(3PL ?), you can use Jacobi+MAP.

11. What if you don't like Jacobi's
result ?
● Too slow ? (initialization, epsilon larger, better 1D algorithm,
better implementation...)
● Epsilon too large ?
● Maybe you use Map whereas you want Bpe ?
==> If you get convergence and don't like the result, it's not because
of Jacobi, it's because of the criterion.
● Maybe not enough data ?

12. Initializing IRT parameters ?
● Roughy approximations for IRT parameters :
– Abilities (Θ)
– Item parameters (a,b,c in 3PL models)
● Priors can be very convenient for that.

13. Find Θ with quantiles !
1. Rank students per performance.

14. Find Θ with quantiles !
2. Cumulative distribution
ABILITIES

15. Find Θ with quantiles !
3. Projections
Medium
student
Best
N/(N+1)
Worst
1/(N+1)
ABILITIES

16. Find Θ with quantiles !
3. Projections
Medium
student
Best
N/(N+1)
Worst
1/(N+1)
ABILITIES

17. Equation version for approximating
abilities Θ
if you have a prior (e.g. Gaussian), then a
simple solution :
– Rank students per score on the test
– For student i over N, Θ initialized at the prior's
quantile 1 – i/(N+1)
E.g. With Gaussian prior mu, sigma,
then ability(i)=mu+sigma*norminv(1-i/(N+1))
With norminv e.g. as in
http://www.wilmott.com/messageview.cfm?
catid=10&threadid=38771

18. Equation version for approximating
item parameters
Much harder !
There are formulas based on correlation. It's a
very rough approximation.
How to estimate b if c=0 ?

19. Approximating item parameters
Much harder !
There are formulas based on correlation. It's a
very rough approximation.
How to estimate b=difficulty if c=0 ?
Simple solution :
– Assume a=1 (discrimination)
– Use the curve, or approximate
b = 4.8 x (1/2 - proba(success))
– If you know students' abilities, it's much easier

20. And for difficulty of items ?
Use curve or approximation...

21. Codes
● IRT in R : there are packages, it's free, and R is
a widely supported language for statistics.
● IRT in Octave : we started our implementation,
but still very preliminary :
– No missing data (the main strength of IRT) ==>
though this would be easy
– No user-friendly interface to data
● Others ? I did not check
● ==> Cross-validation for comparing ?

22. How to get the percentile from the
ability
● percentile is norm-cdf( (theta*-mu)/sigma).
(some languages have normcdf included)
● Slow/precise implementation of norm-cdf:
http://stackoverflow.com/questions/2328258/cumula
● Fast implementation of norm-cdf:
http://finance.bi.no/~bernt/gcc_prog/recipes/recipes
● Maybe fast Exp, if you want to save up time :-)