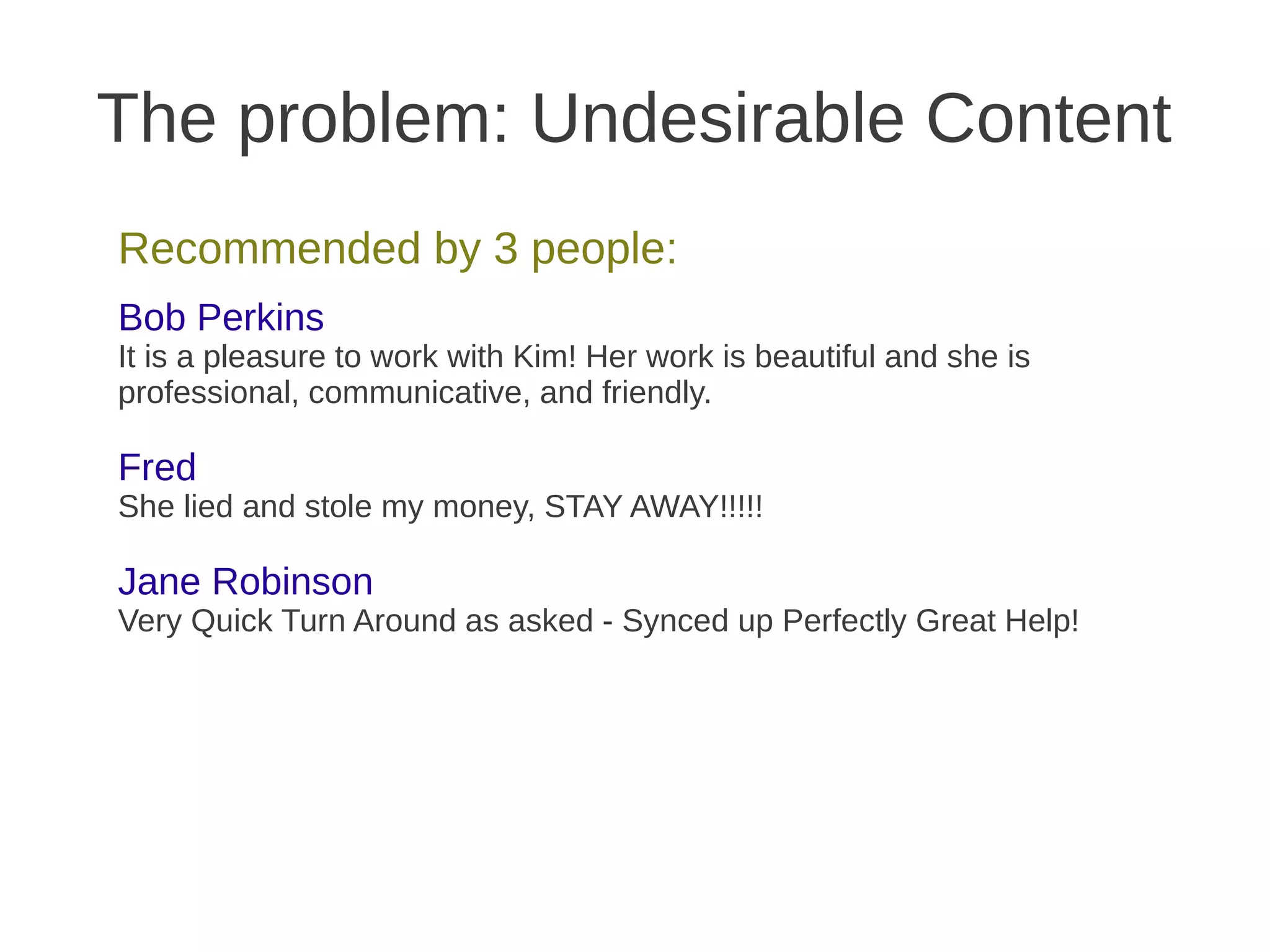
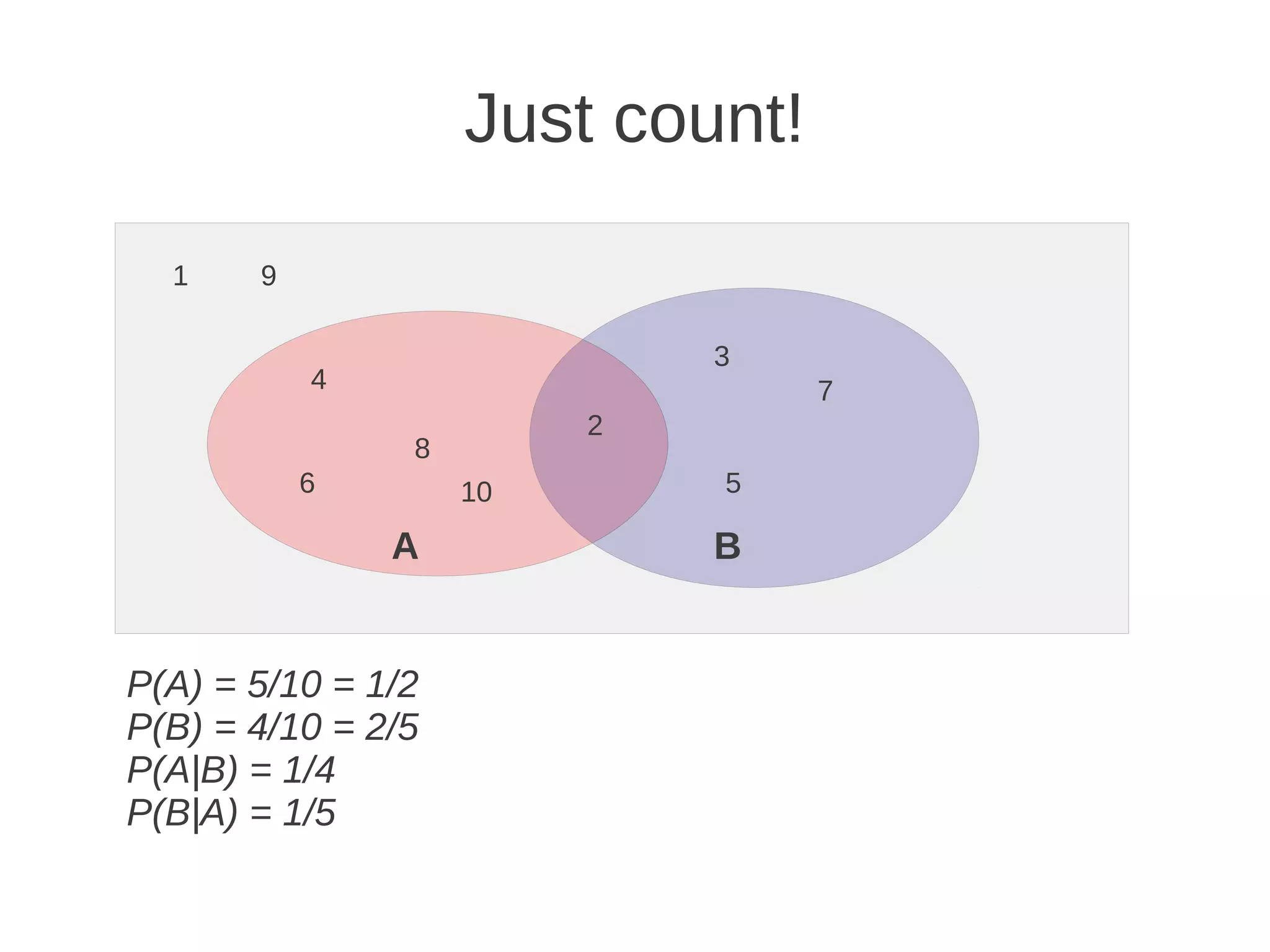
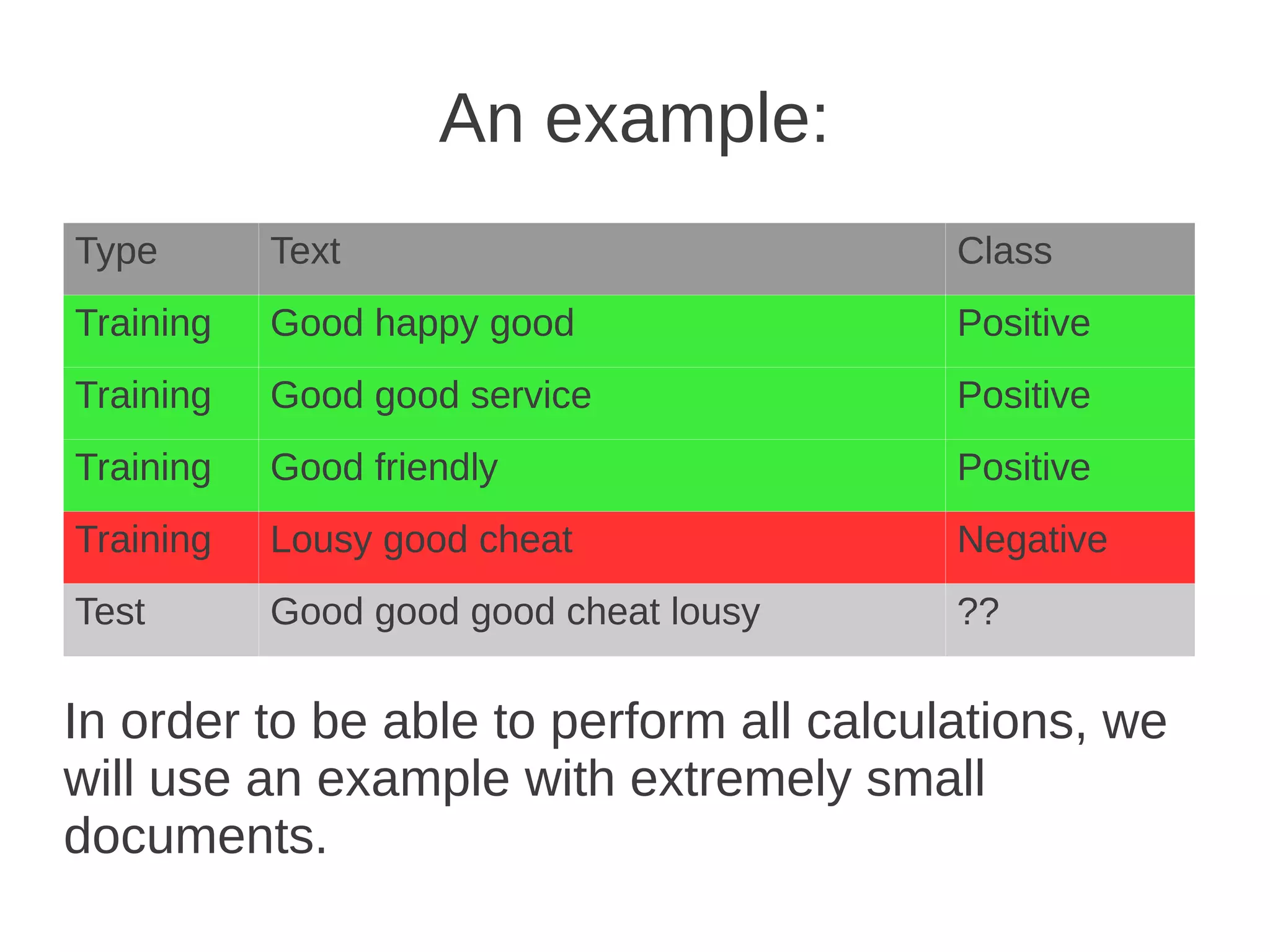
The document discusses building a Naive Bayes classifier to filter undesirable content, detailing steps such as manually removing content, using banned word lists, and applying machine learning algorithms. It explains key concepts of probability, Bayes' theorem, tokenization challenges, and the training process for the classifier, along with practical considerations like smoothing and evaluating classifier performance. Eric Wilson also provides his contact information for further inquiries.

1. Building a Naive Bayes Classifier
Eric Wilson
Search Engineer
Manta Media

2. The problem: Undesirable Content
Recommended by 3 people:
Bob Perkins
It is a pleasure to work with Kim! Her work is beautiful and she is
professional, communicative, and friendly.
Fred
She lied and stole my money, STAY AWAY!!!!!
Jane Robinson
Very Quick Turn Around as asked - Synced up Perfectly Great Help!

3. Possible solutions
● First approach: manually remove undesired
content.
● Attempt to filter based on lists of banned
words.
● Use a machine learning algorithm to identify
undesirable content based on a small set of
manually classified examples.

4. Using Naive Bayes isn't too hard!
● We'll need a bit of probability, including the
concept of conditional probability.
● A few natural language processing ideas will
be necessary.
● Facility with any modern programming
language.
● Persistence with many details.

5. Probability 101
Suppose we choose a number from the set:
U = {1,2,3,4,5,6,7,8,9,10}
Let A be the event that the number is even,
and B be the event that the number is prime.
Compute P(A), P(B), P(A|B), and P(B|A),
where P(A|B) is the probability of A given B.

6. Just count!
1 9
3
4 7
2
8
6 10 5
A B
P(A) = 5/10 = 1/2
P(B) = 4/10 = 2/5
P(A|B) = 1/4
P(B|A) = 1/5

7. Bayes Theorem
P(A|B) = P(AB)/P(B)
P(B)P(A|B) = P(AB)
P(B)P(A|B) = P(A)P(B|A)
P(A|B) = P(A)P(B|A)/P(B)

8. A simplistic language model
Consider each document to be a set of words,
along with frequencies.
For example: “The premium quality for the
discount price” is viewed as:
{'the':2, 'premium':1, 'quality':1, 'for':1,
'discount':1, 'price':1}
Same as “The discount quality for the premium
price,” since we don't care about order.

9. That seems … foolish
● English is so complicated that we won't have
any real hope of understanding semantics.
● In many real-life scenarios, text that you want
to classify is not exactly subtle.
● If necessary, we can improve our language
model later.

10. An example:
Type Text Class
Training Good happy good Positive
Training Good good service Positive
Training Good friendly Positive
Training Lousy good cheat Negative
Test Good good good cheat lousy ??
In order to be able to perform all calculations, we
will use an example with extremely small
documents.

11. What was the question?
We are trying to determine whether the last
recommendation was positive or negative.
We want to compute:
P(Pos|good good good lousy cheat)
By Bayes Theorem, this is equal to:
P(Pos)P(good good good lousy cheat|Pos)
P(good good good lousy cheat)

12. What do we know?
P(Pos) = 3/4
P(good|Pos), P(cheat|Pos), P(lousy|Pos)
Are all easily computed by counting using the
training set.
Which is almost what we want ...

13. Wouldn't it be nice ...
Maybe we have all we need? Isn't
P(good good good lousy cheat|Pos) =
P(good|Pos)3P(lousy|Pos)P(cheat|Pos) ?
Well, yes, if these are independent events,
which almost certainly doesn't hold.
The “naive” assumption is that we can
consider these events independent.

14. The Naive Bayes Algorithm
If C1,C2,...,Cn are classes, and an instance has
features F1,F2,...,Fm, then the most likely class
for this instance is the one that maximizes the
following:
P(Ci )P(F1|Ci )P(F2|Ci )...P(Fm|Ci )

15. Wasn't there a denominator?
If our goal was to compute the probability of
the most likely class, we should divide by:
P(F1)P(F2)...P(Fm)
We can ignore this part because, we only care
about which class has the highest probability,
and this term is the same for each class.

16. Interesting theory but …
Won't this break as soon as we encounter a
word that isn't in our training set?
For example, if “goood” is not in our training
set, and occurs in our test set, then since
P(Pos|goood) = 0, so our product is zero for all
classes.
We need nonzero probabilities for all words,
even words that don't exist.

17. Plus-one smoothing
Just count every word one time more than it
actually occurs.
Since we are only concerned with relative
probabilities, this inaccuracy should be of no
concern.
P(word|C) = count(word|C) + 1
count(C) + V
(V is the total vocabulary, so that our
probabilities sum to 1.)

18. Let's try it out:
P(Pos) = ¾ Type Text Class
P(Neg) = ¼ Training Good happy good Positive
Good good service Positive
Good friendly Positive
Lousy good cheat Negative
Test Good good good cheat lousy ??
P(good|Pos) = (5+1)/(8+6) = 3/7
P(cheat|Pos) = (0+1)/(8+6) = 1/14 P(Pos|D5) ~ ¾ * (3/7)3*(1/14)*(1/14)
P(lousy|Pos) = (0+1)/(8+6) = 1/14 = 0.0003
P(good|Neg) = (1+1)/(3+6) = 2/9 P(Neg|D5) ~ ¼ * (2/9)3*(2/9)*(2/9)
P(cheat|Neg) = (1+1)/(3+6) = 2/9 = 0.0001
P(lousy|Neg) = (1+1)/(3+6) = 2/9

19. Training the classifier
● Count instances of classes, store counts in a map.
● Store counts of all words in a nested map:
{'pos':
{'good': 5, 'friendly': 1, 'service': 1, 'happy': 1},
'neg':
{'cheat': 1, 'lousy': 1, 'good': 1}
}
● Should be easy to compute probabilities.
● Should be efficient (training time and memory.)

20. Some practical problems
● Tokenization
● Arithmetic
● How to evaluate results?

21. Tokenization
● Use whitespace?
– “food”, “food.”, food,” and “food!” all different.
● Use whitespace and punctuation?
– “won't” tokenized to “won” and “t”
● What about emails? Urls? Phone numbers?
What about the things we haven't thought
about yet?
● Use a library. Lucene is a good choice.

22. Arithmetic
What happens when you multiply a large
amount of small numbers?
To prevent underflow, use sums of logs instead
of products of true probabilities.
Key properties of log:
● log(AB) = log(A) + log(B)
● x > y => log(x) > log(y)
● Turns very small numbers into managable negative
numbers

23. Evaluating a classifier
● Precision and recall
● Confusion matrix
● Divide training set into nine “folds”, train
classifier on nine folds, and check accuracy of
classifying the tenth fold

24. Experiment
● Tokenization strategies
– Stop words
– Capitalization
– Stemming
● Language model
– Ignore multiplicities
– Smoothing

25. Contact me
● wilson.eric.n@gmail.com
● ewilson@manta.com
● @wilsonericn
● http://wilsonericn.wordpress.com