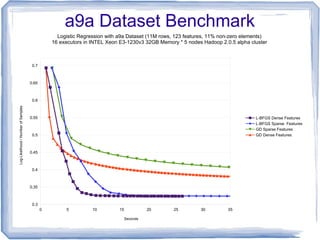
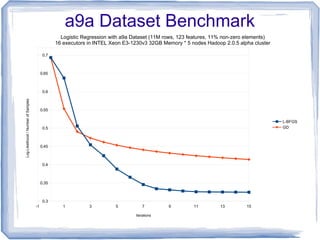
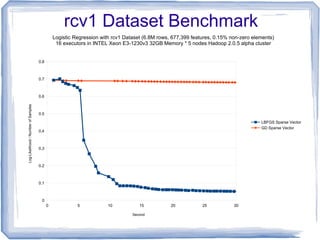
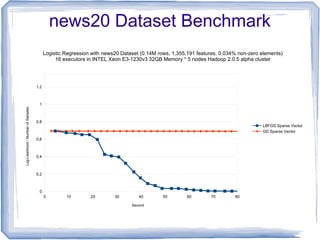
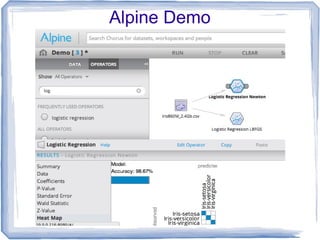
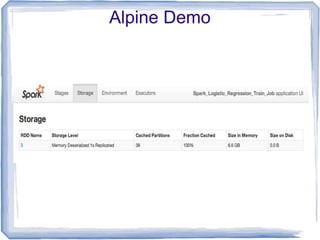
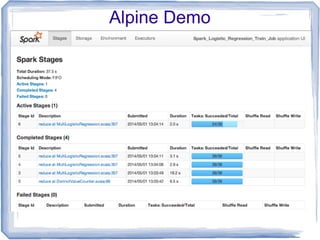
The document discusses the implementation of multinomial logistic regression using Apache Spark, highlighting its advantages over traditional Hadoop MapReduce for machine learning tasks by providing faster and more efficient model training. It details the optimization techniques, such as maximum likelihood estimation and various minimization approaches, alongside a comparison of logistic regression performance on different datasets. Additionally, it addresses challenges like overfitting and regularization, while presenting API options available in Spark for distributed data processing.





![Problem of Second Order Minimizer
● Scale horizontally (the numbers of training
data) by leveraging Spark to parallelize this
iterative optimization process.
● Don't scale vertically (the numbers of training
features). Dimension of Hessian is
● Recent applications from document
classification and computational linguistics are
of this type.
dim(H )=[(k−1)(n+1)]
2
where k is numof class ,nis num of features](https://image.slidesharecdn.com/2014-05-01mlor-140505025944-phpapp01/85/Multinomial-Logistic-Regression-with-Apache-Spark-7-320.jpg)






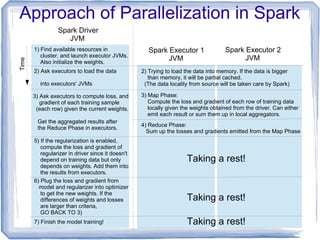
![Mini School of Spark APIs
● mapPartitions(func) : Similar to map, but runs
separately on each partition (block) of the
RDD, so func must be of type Iterator[T] =>
Iterator[U] when running on an RDD of type T.
● This API allows us to have global variables on
entire partition to aggregate the result locally
and efficiently.](https://image.slidesharecdn.com/2014-05-01mlor-140505025944-phpapp01/85/Multinomial-Logistic-Regression-with-Apache-Spark-15-320.jpg)



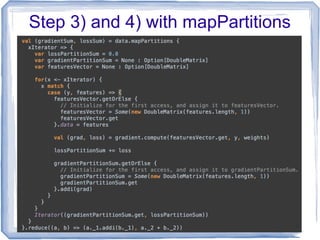

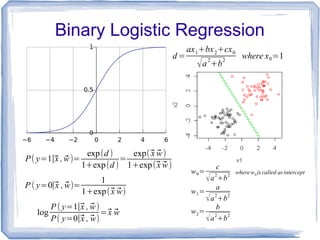
![Extension to Multinomial Logistic Regression
● In Binary Logistic Regression
● For K classes multinomial problem where labels
ranged from [0, K-1], we can generalize it via
● The model, weights becomes
(K-1)(N+1) matrix, where N is number of features.
log
P( y=1∣⃗x , ̄w)
P ( y=0∣⃗x , ̄w)
=⃗x ⃗w1
log
P ( y=2∣⃗x , ̄w)
P ( y=0∣⃗x , ̄w)
=⃗x ⃗w2
...
log
P ( y=K −1∣⃗x , ̄w)
P ( y=0∣⃗x , ̄w)
=⃗x ⃗wK −1
log
P( y=1∣⃗x , ⃗w)
P ( y=0∣⃗x , ⃗w)
=⃗x ⃗w
̄w=(⃗w1, ⃗w2, ... , ⃗wK −1)T
P( y=0∣⃗x , ̄w)=
1
1+∑
i=1
K −1
exp(⃗x ⃗wi )
P( y=1∣⃗x , ̄w)=
exp(⃗x ⃗w2)
1+∑
i=1
K −1
exp(⃗x ⃗wi)
...
P( y=K −1∣⃗x , ̄w)=
exp(⃗x ⃗wK −1)
1+∑i=1
K −1
exp(⃗x ⃗wi )](https://image.slidesharecdn.com/2014-05-01mlor-140505025944-phpapp01/85/Multinomial-Logistic-Regression-with-Apache-Spark-22-320.jpg)