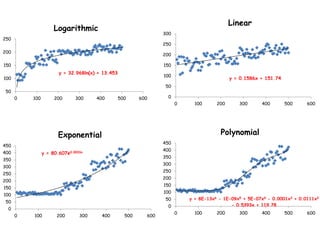
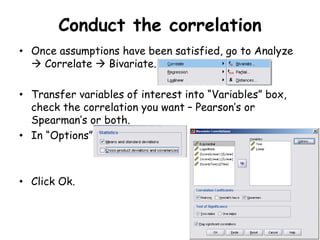
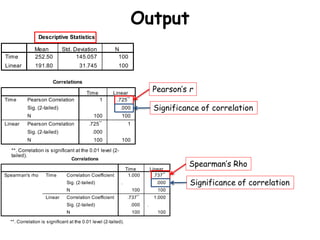
This document discusses correlations and how to perform them using SPSS. It defines correlation as finding a relationship between two variables, without implying causation. There are two parts to a correlation analysis: 1) assessing the significance of the correlation, which indicates how consistent the association is between variables, and 2) the coefficient of correlation, which indicates the magnitude and direction of the correlation. The document outlines the assumptions that must be met to perform correlations in SPSS, such as having quantitative variables, no outliers, and normally distributed data. It then provides step-by-step instructions for conducting correlations in SPSS and interpreting the output.

1. Inferential Statistics
Correlations
Dhritiman Chakrabarti
Assistant Professor,
Dept of Neuroanaesthesiology
and Neurocritical Care,
NIMHANS, Bangalore

2. What is Correlation
• Trying to find a relationship/association between two
variables is called correlation.
• Does not signify the direction of relationship  in
that you cannot predict the causation from predictor
to outcome variable  That is regression.
• Relationship between two variables can be described
by mathematic formulae which describe the
relationship. Some common relationships are linear,
logistic, exponential, quadratic, cubic and so on.
• For our purposes, the only important relationship that
we test for is linear. If data follows some other curve
in scatter plot, better to go for curve fitting –
advanced stats.

3. y = 32.968ln(x) + 13.453
50
100
150
200
250
0 100 200 300 400 500 600
Logarithmic
y = 0.1586x + 151.74
0
50
100
150
200
250
300
0 100 200 300 400 500 600
Linear
y = 80.607e0.0033x
0
50
100
150
200
250
300
350
400
450
0 100 200 300 400 500 600
Exponential
y = 8E-13x6 - 1E-09x5 + 5E-07x4 - 0.0001x3 + 0.0111x2
- 0.5393x + 119.780
50
100
150
200
250
300
350
400
450
0 100 200 300 400 500 600
Polynomial

4. Types of Correlations
So, essentially there are two parts of a correlation analysis:
1. Significance of correlation  Tells about consistency of association between
one variable and other.
2. Coefficient of correlation  Tells about magnitude and direction of
correlation between one variable and other.

5. How to do correlations
• Normally in biological sciences, correlations are
performed for measuring association between interval
and/or ordinal type variables, or as bivariate analysis
for inclusion/exclusion from regression model.
• Manual calculation is a bit lengthy. No point in going
into it.
• Correlation Coefficient can be seen as change in one
variable with unit change in other – in a bivariate
manner.
• Regression in change in dependent variable with unit
change in independent. Reg coeff changes if dep and
indep are reversed.
• But standardized coeff of univariate linear regression
with single predictor is same as pearson’s correlation
coeff.

6. How to on SPSS
• Assumptions:
1. Quantitative variable (for Pearson’s)  In Ordinal
use Spearman’s correlation (non-parametric equiv of
Pearson’s)
2. Pair of variables to be analyzed per case.
3. Absence of outliers  Outlier is >3.29 SD away
from mean.
4. Variables be normally distributed  Use Shapiro
Wilk  If not normal, use Spearman’s.
5. Linear relationship on scatter plot.

7. Checking for Outliers
• Go to Analyze  Descriptive statisctics  Descriptives 
Insert variables for correlation into “Variables”
• Check
• Click OK.
• No use of the output other than descriptives. You will see 2 new
columns formed in the data sheet  These are the standardized
normal deviates (Z-scores) of the variables. Check if any are ≥
±3.29, and delete them  These can skew a Pearson’s r.

8. Conduct the correlation
• Once assumptions have been satisfied, go to Analyze
 Correlate  Bivariate.
• Transfer variables of interest into “Variables” box,
check the correlation you want – Pearson’s or
Spearman’s or both.
• In “Options”
• Click Ok.

9. Output
Pearson’s r
Significance of correlation
Spearman’s Rho
Significance of correlation