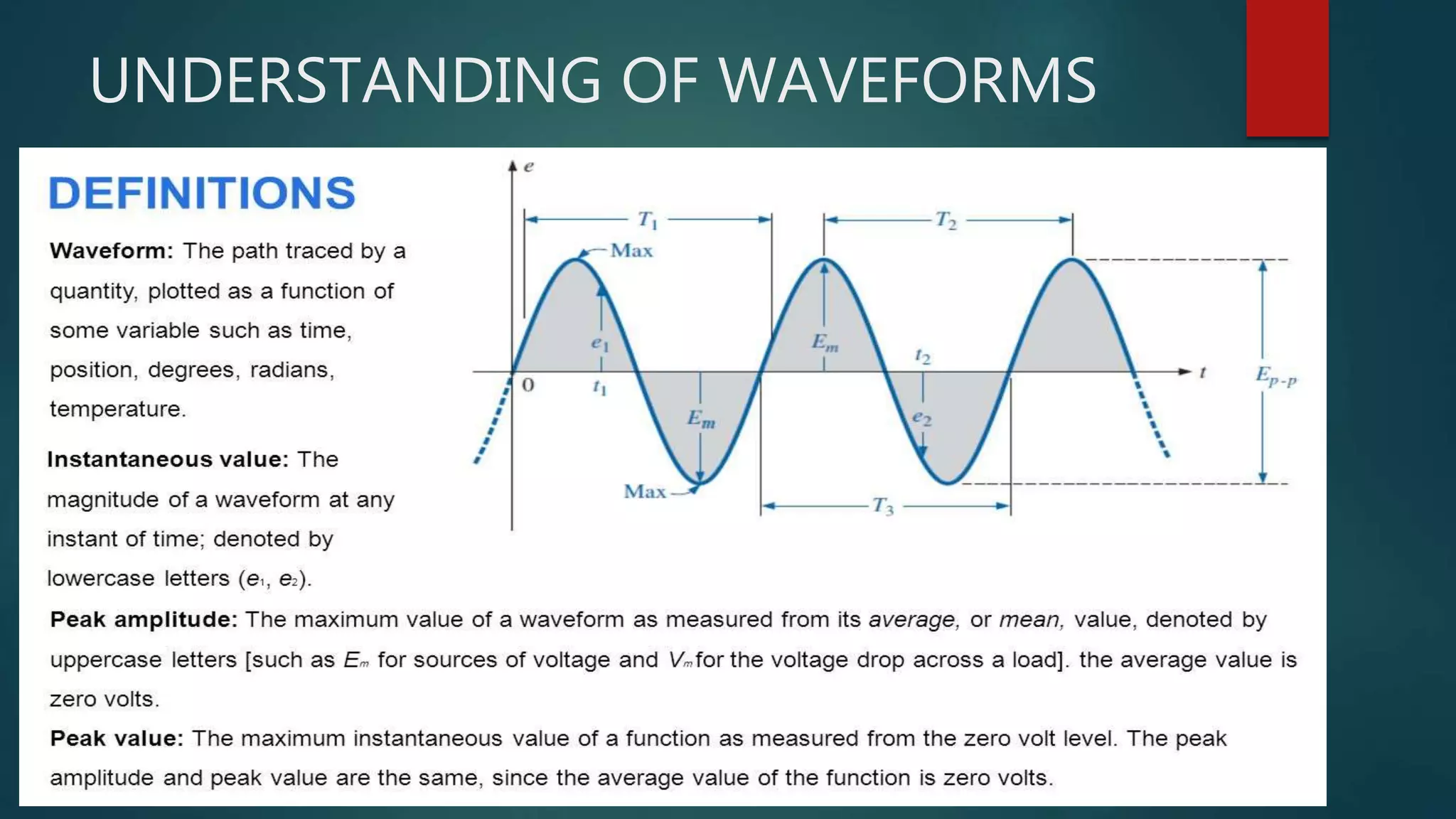
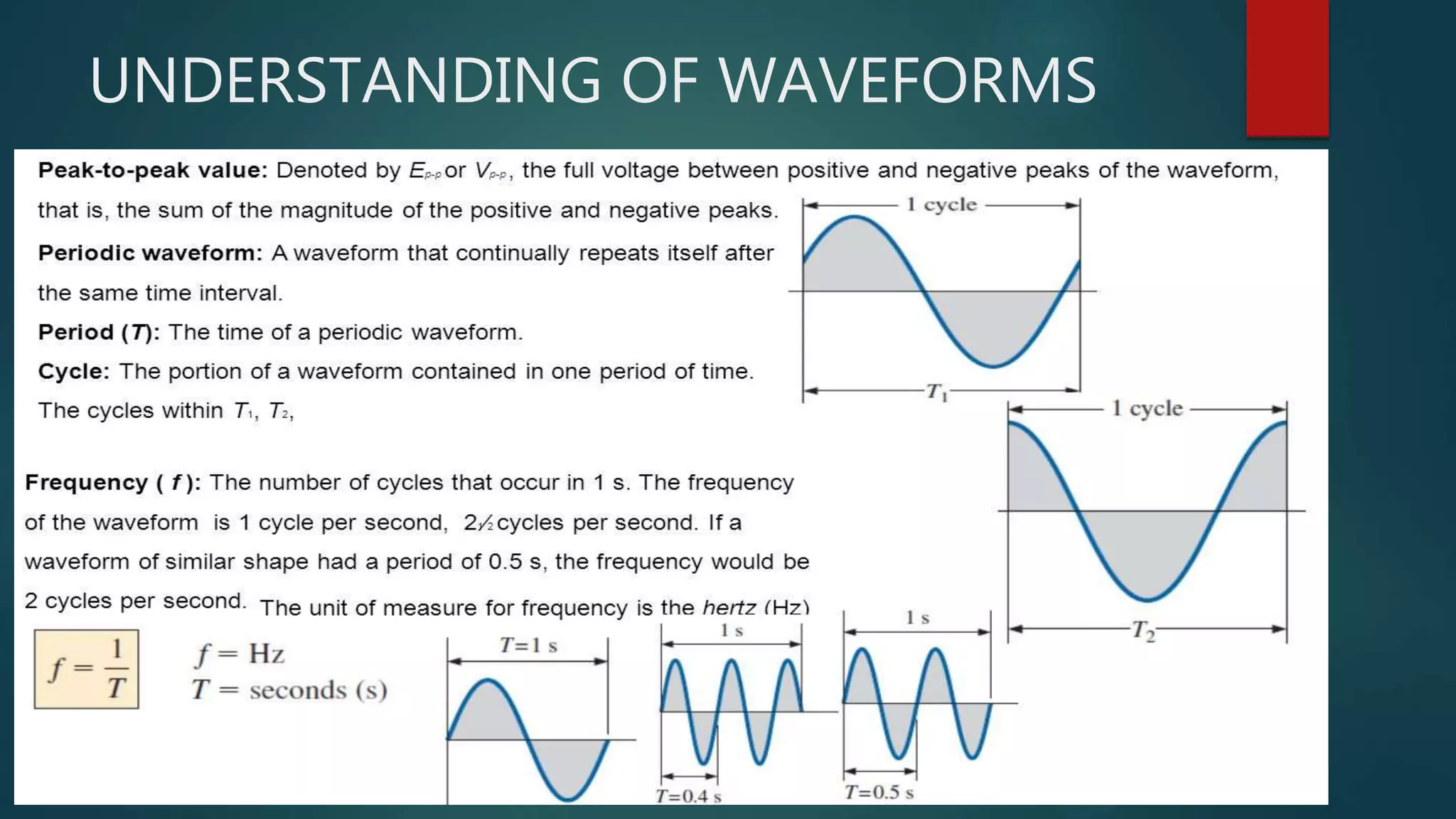
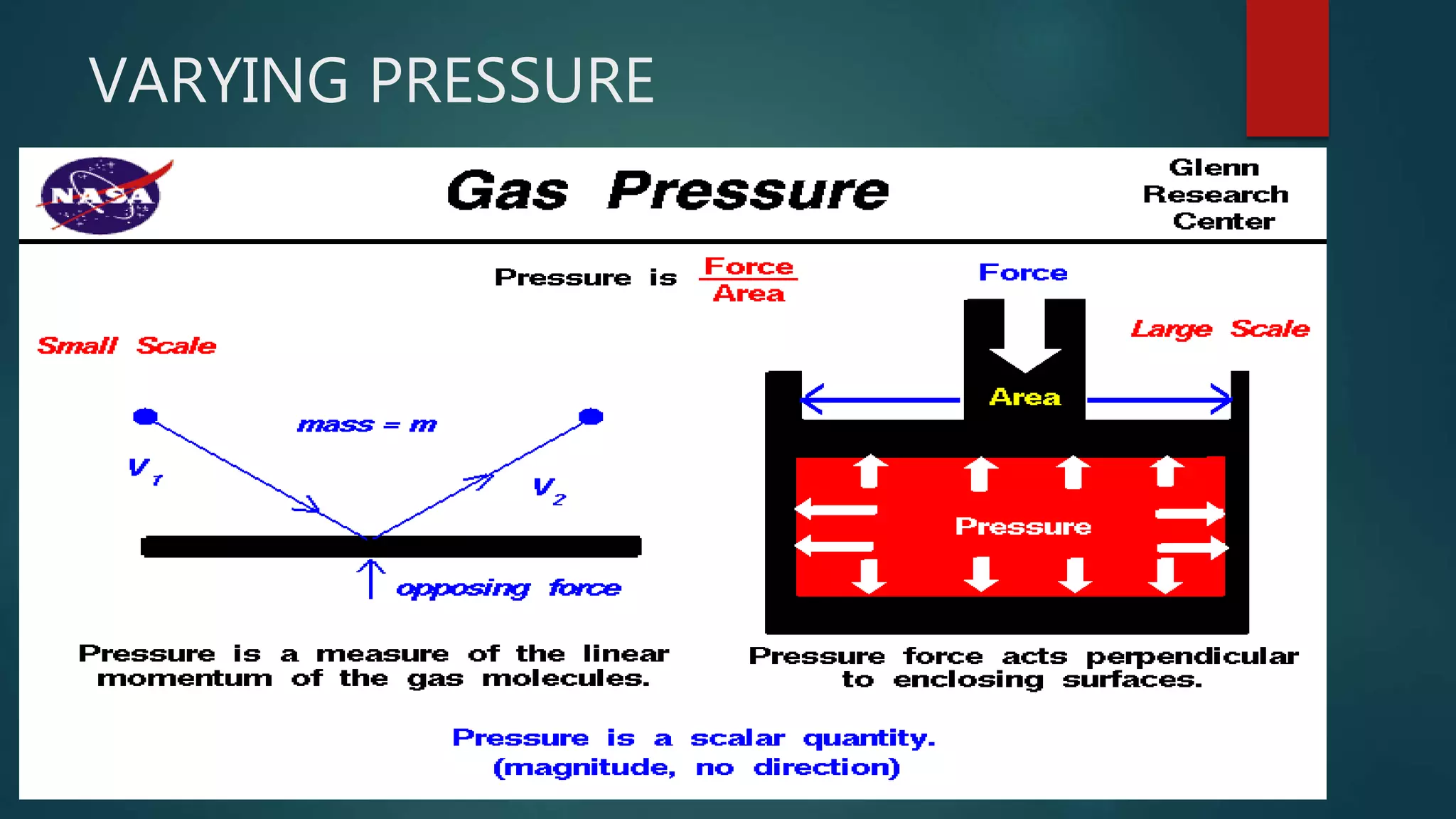
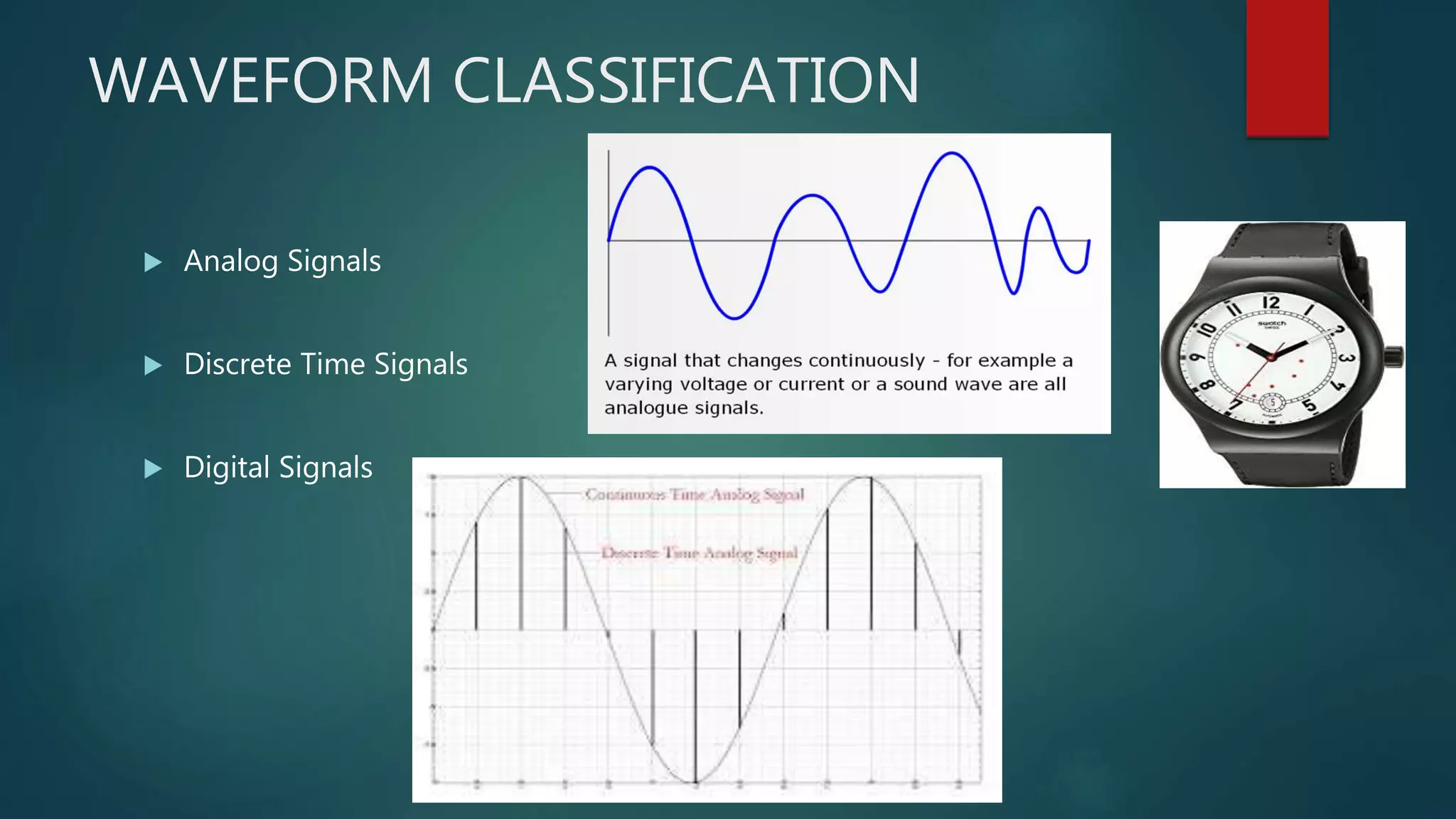
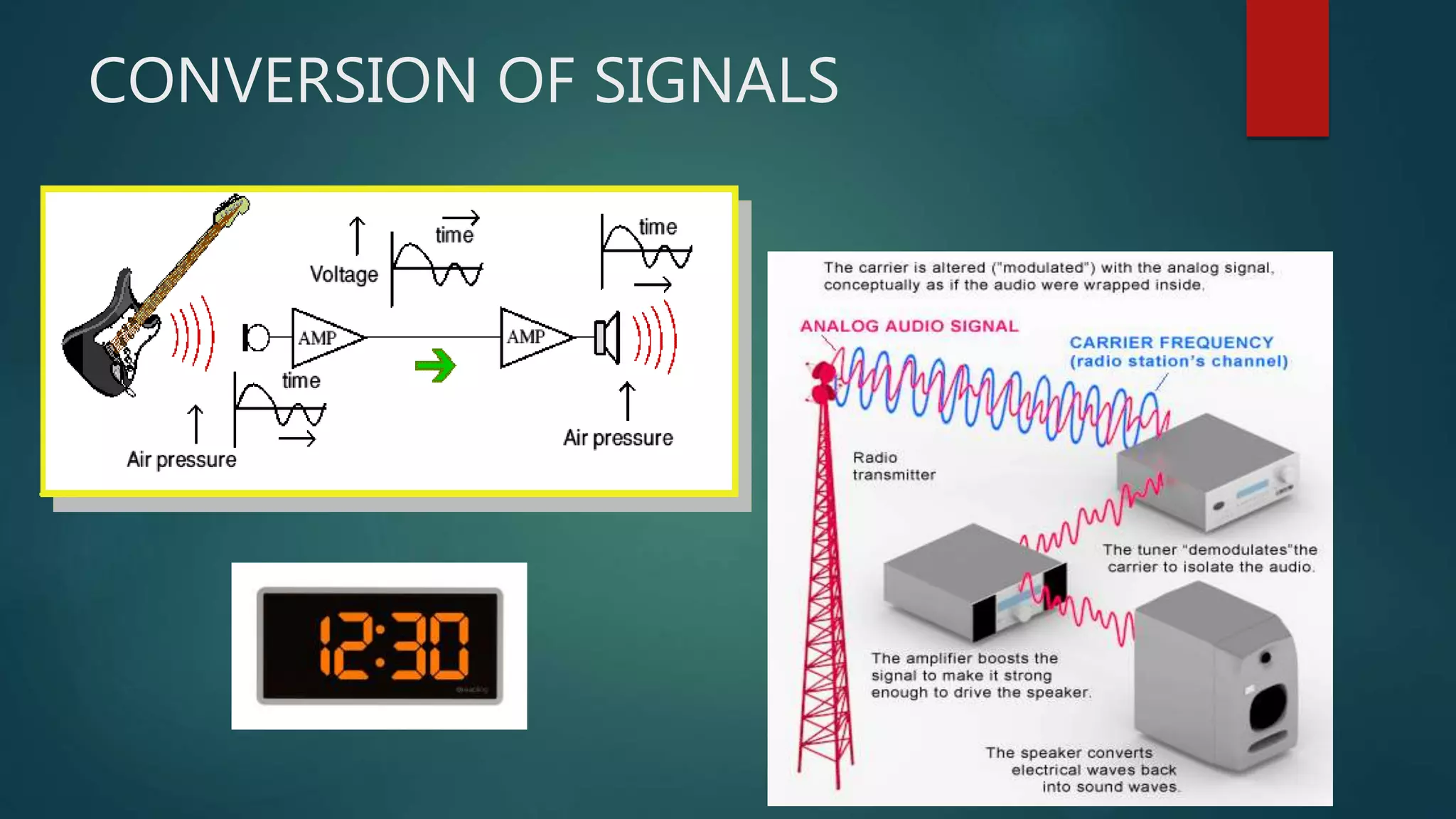
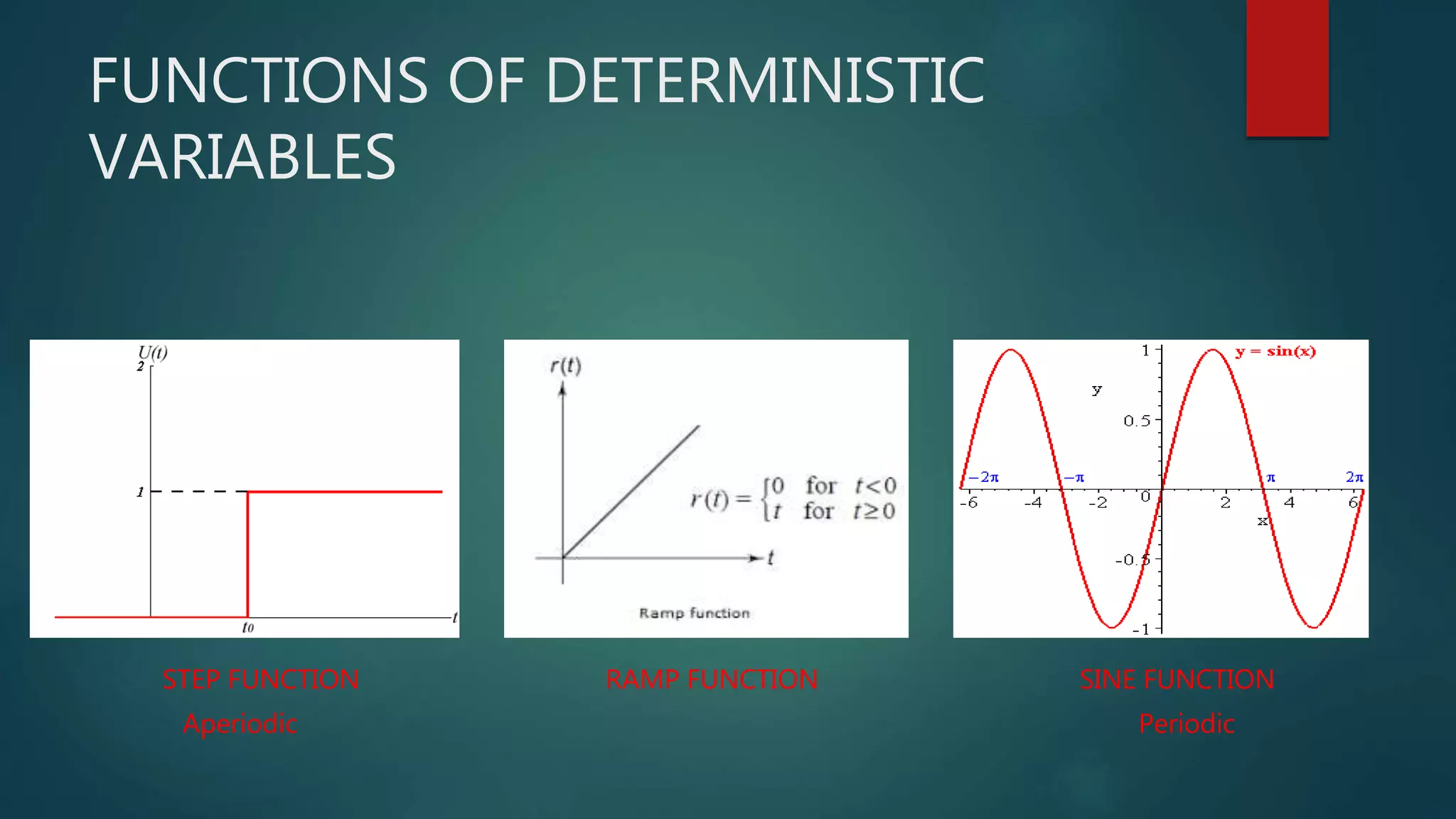
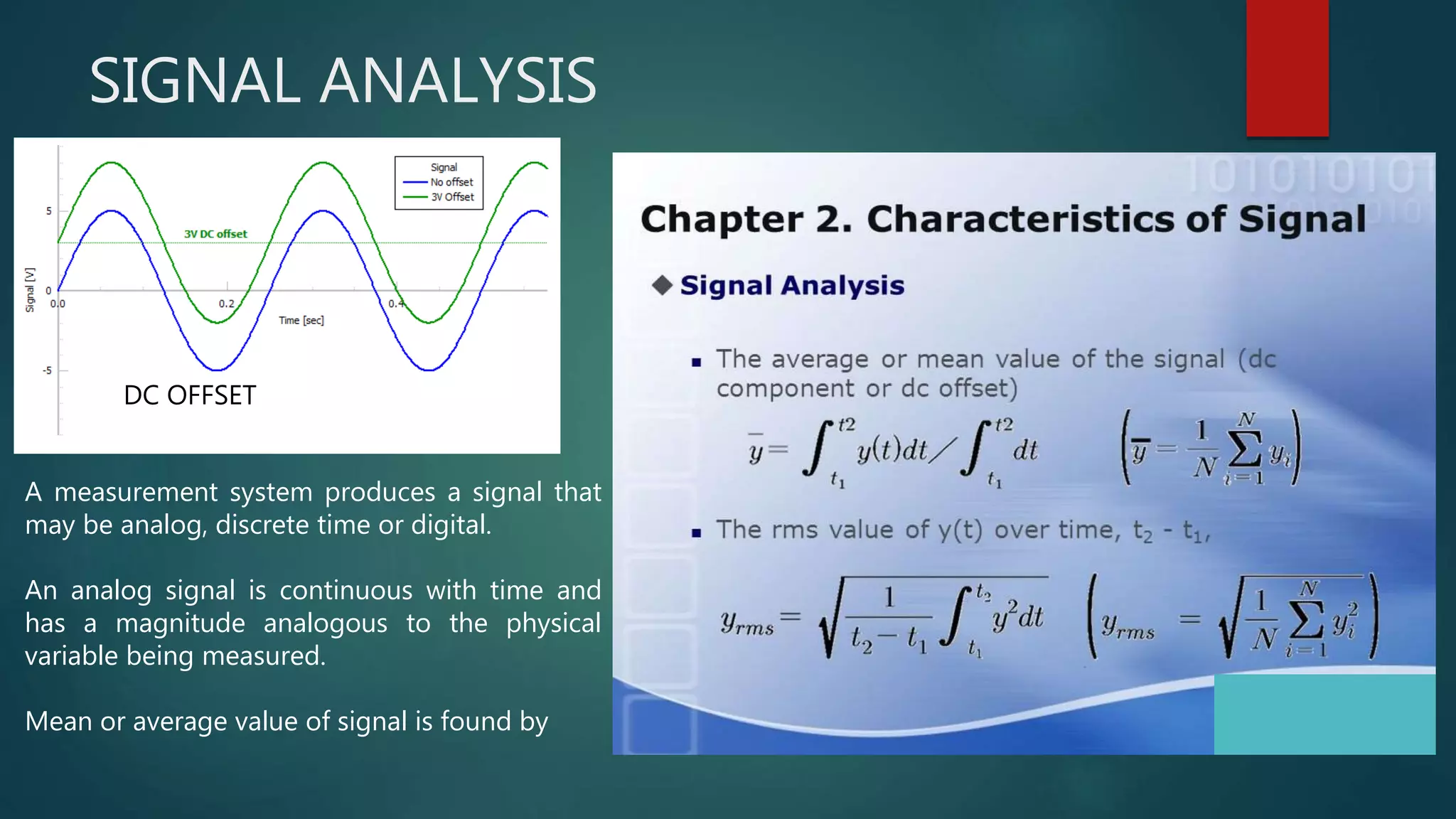
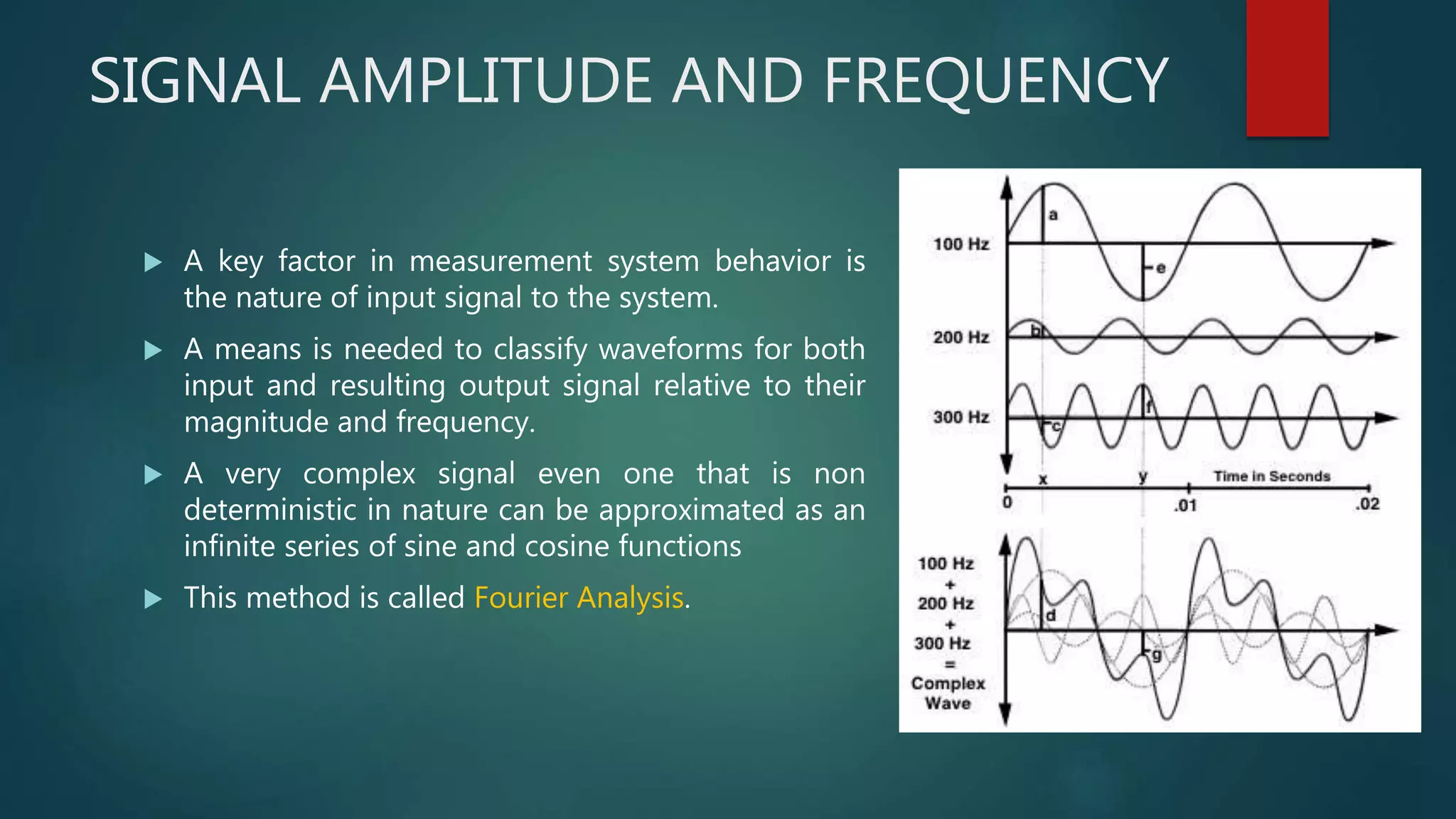
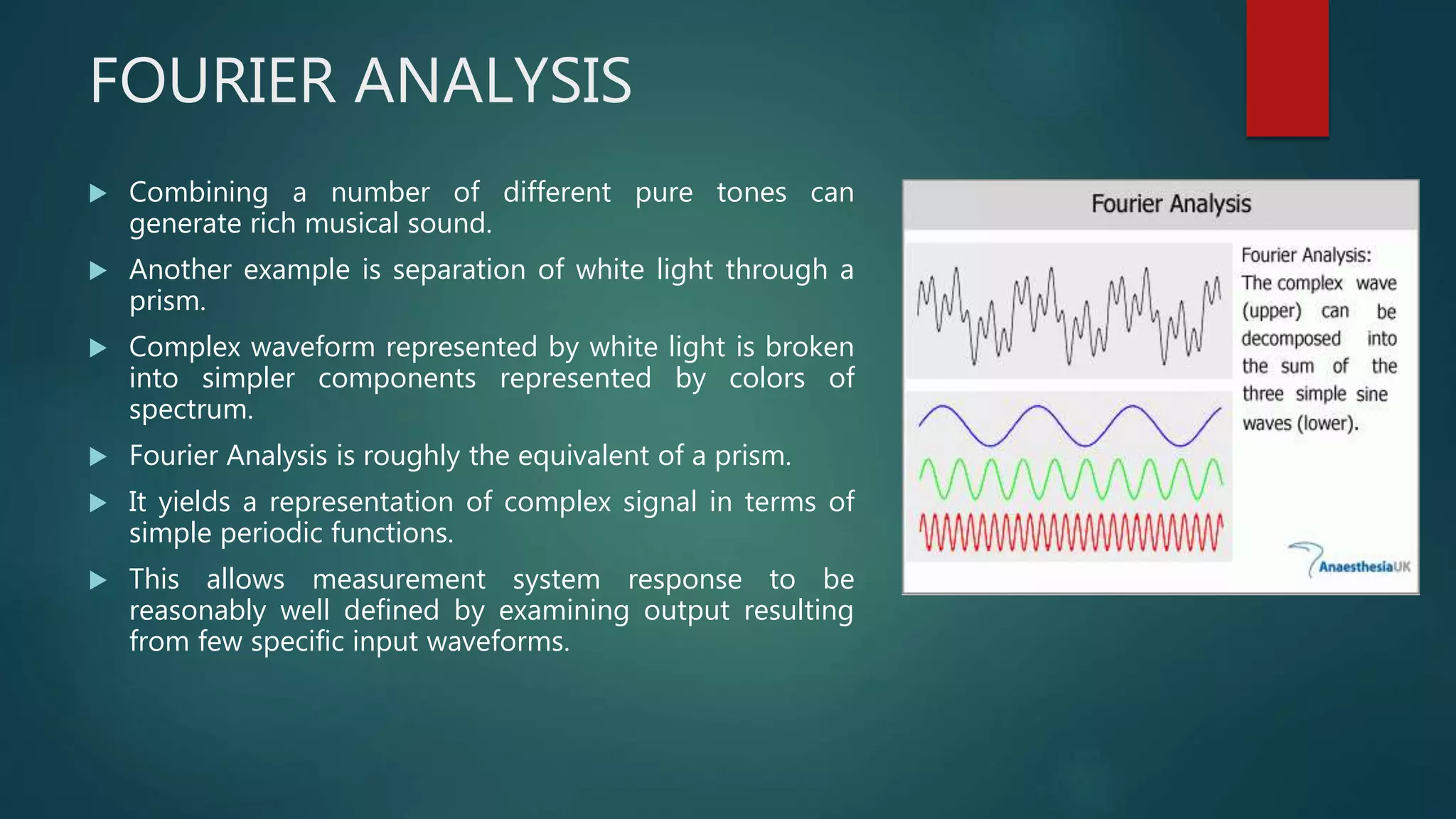
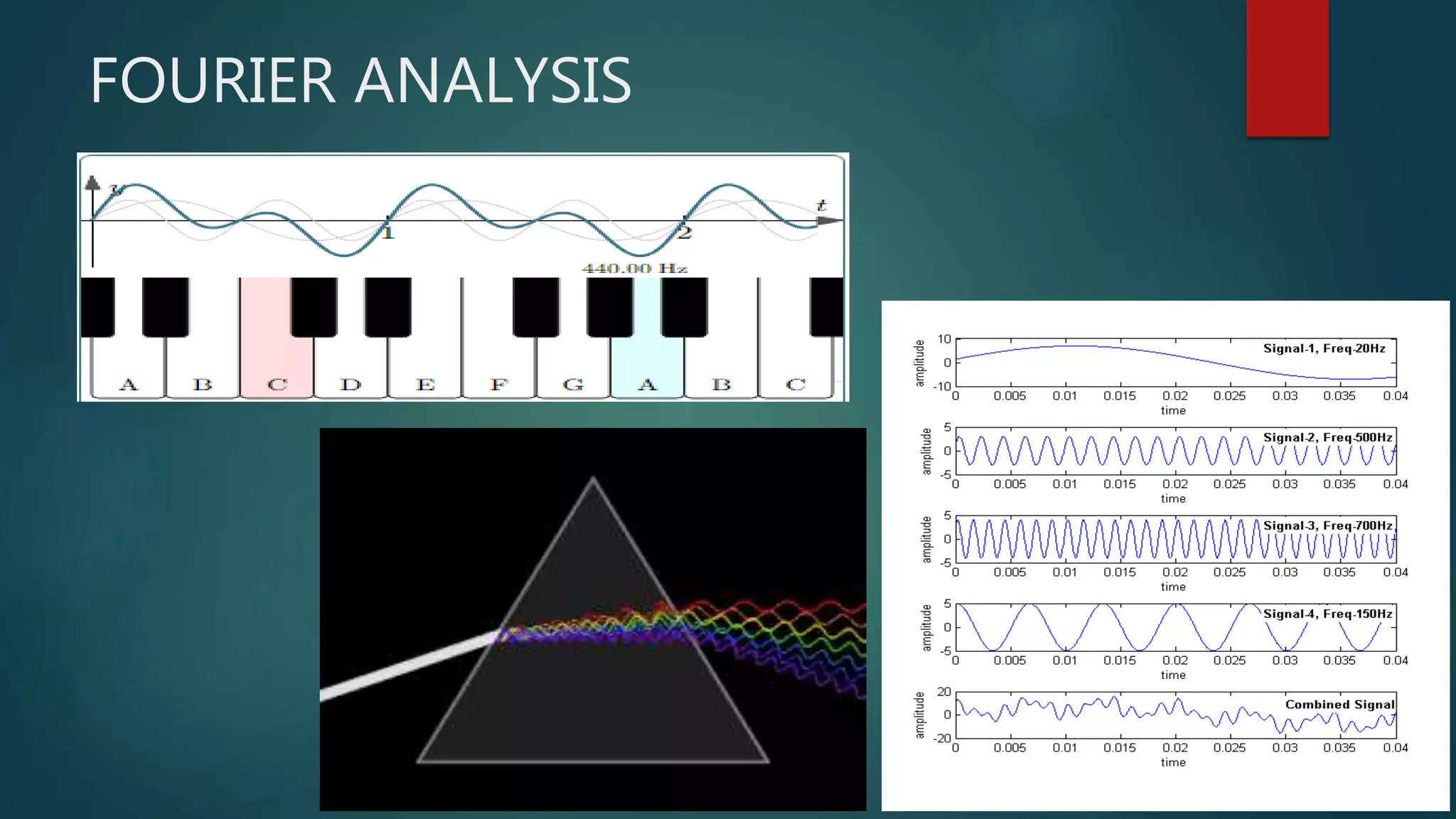
Chapter 2 of 'Theory and Design for Mechanical Measurements' discusses the characteristics of signals in measurement systems, focusing on static and dynamic signals, waveforms, and classifications such as deterministic and non-deterministic signals. It emphasizes the importance of understanding input and output signals for effective measurement and analysis, including the use of Fourier analysis to decompose complex signals into simpler components. The chapter concludes with exercises that reinforce the concepts presented.