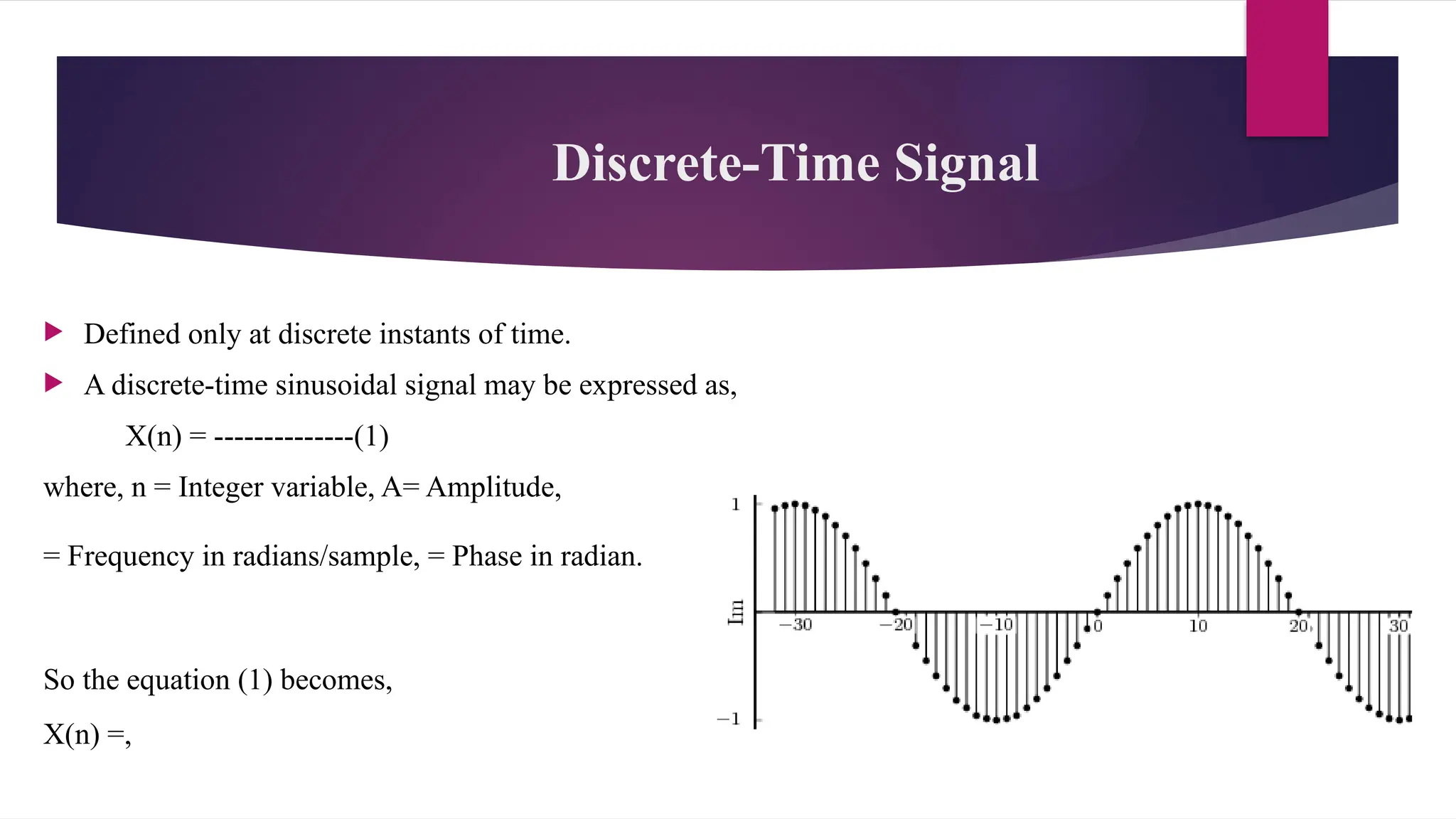
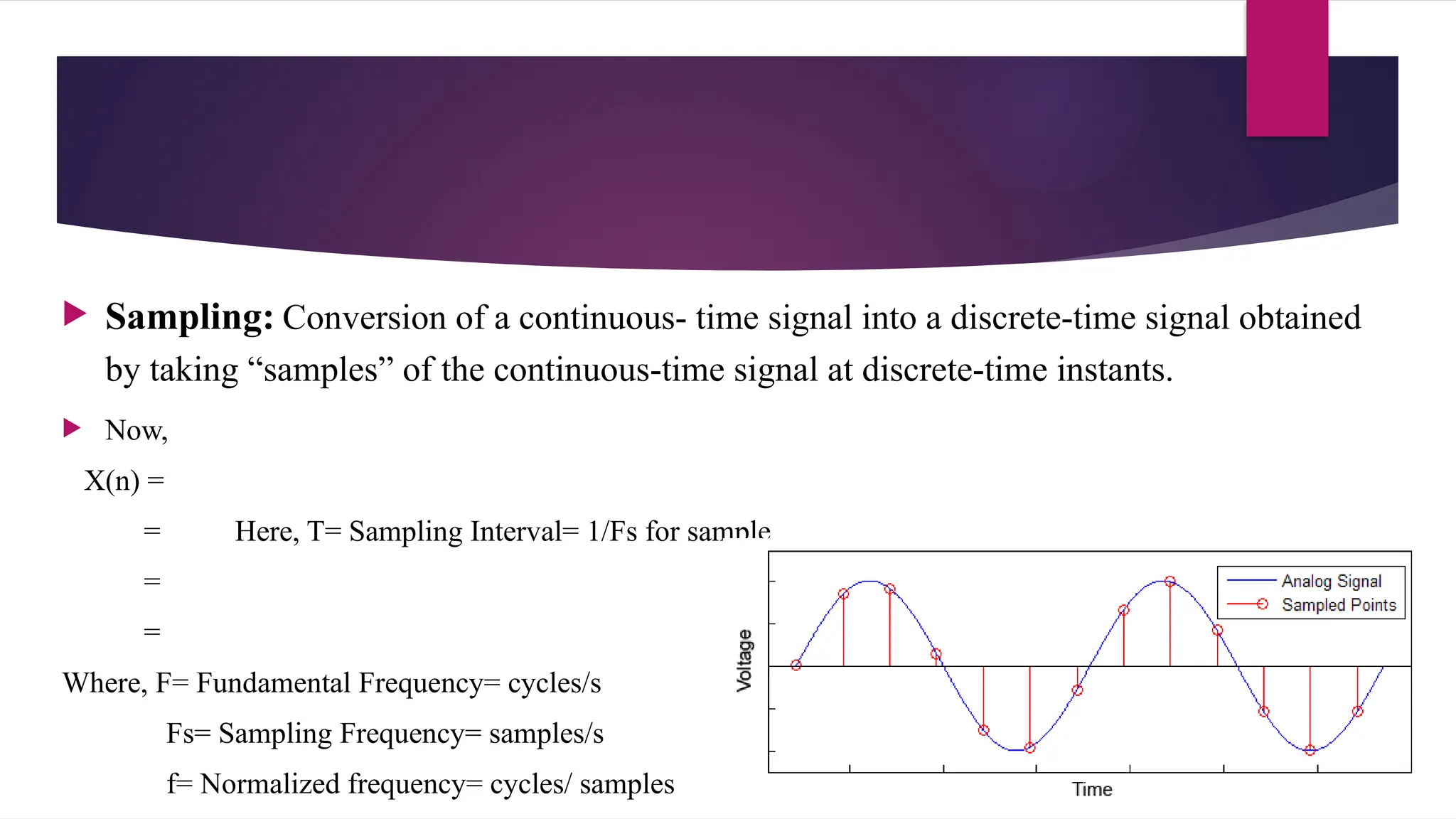
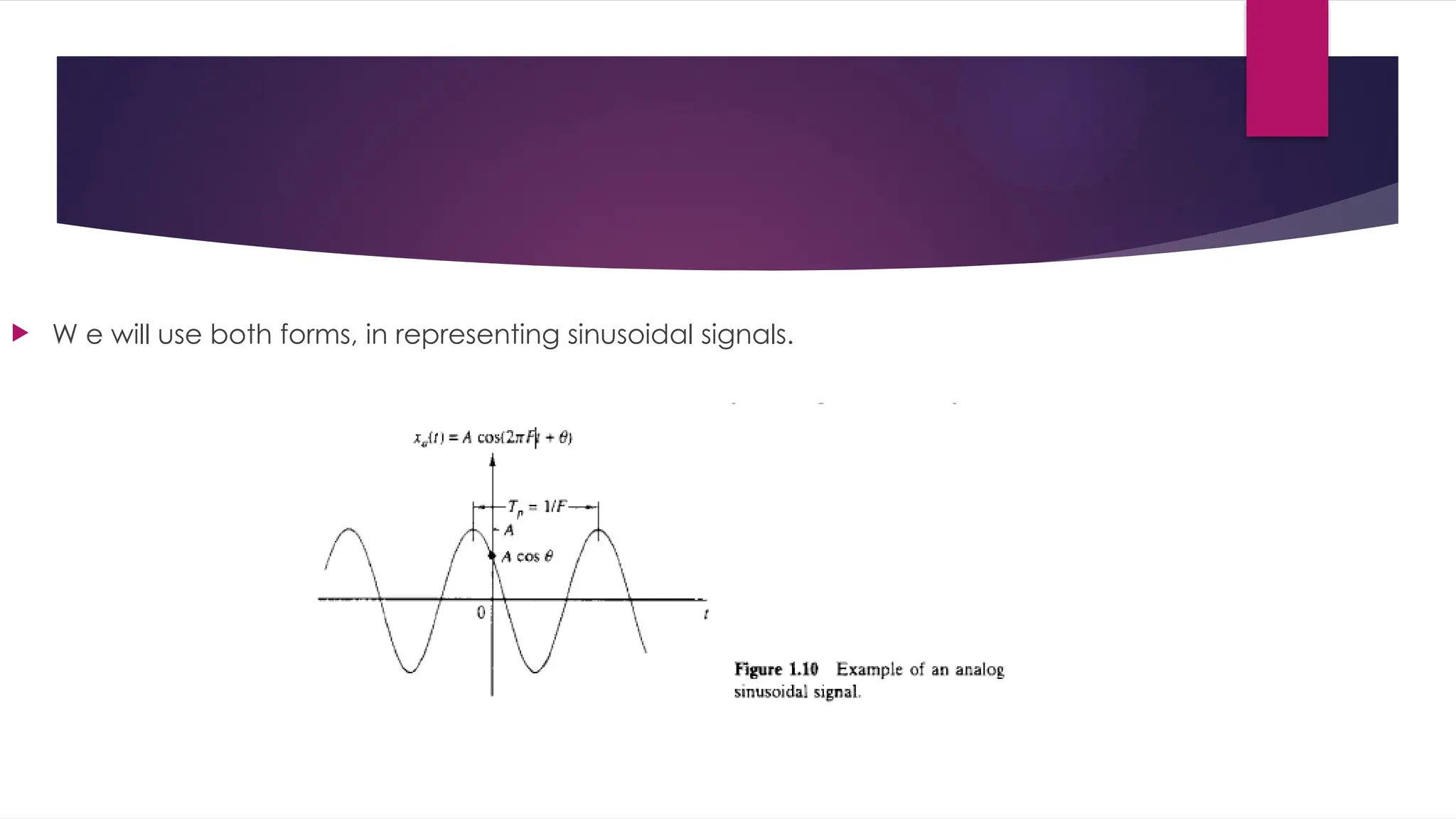
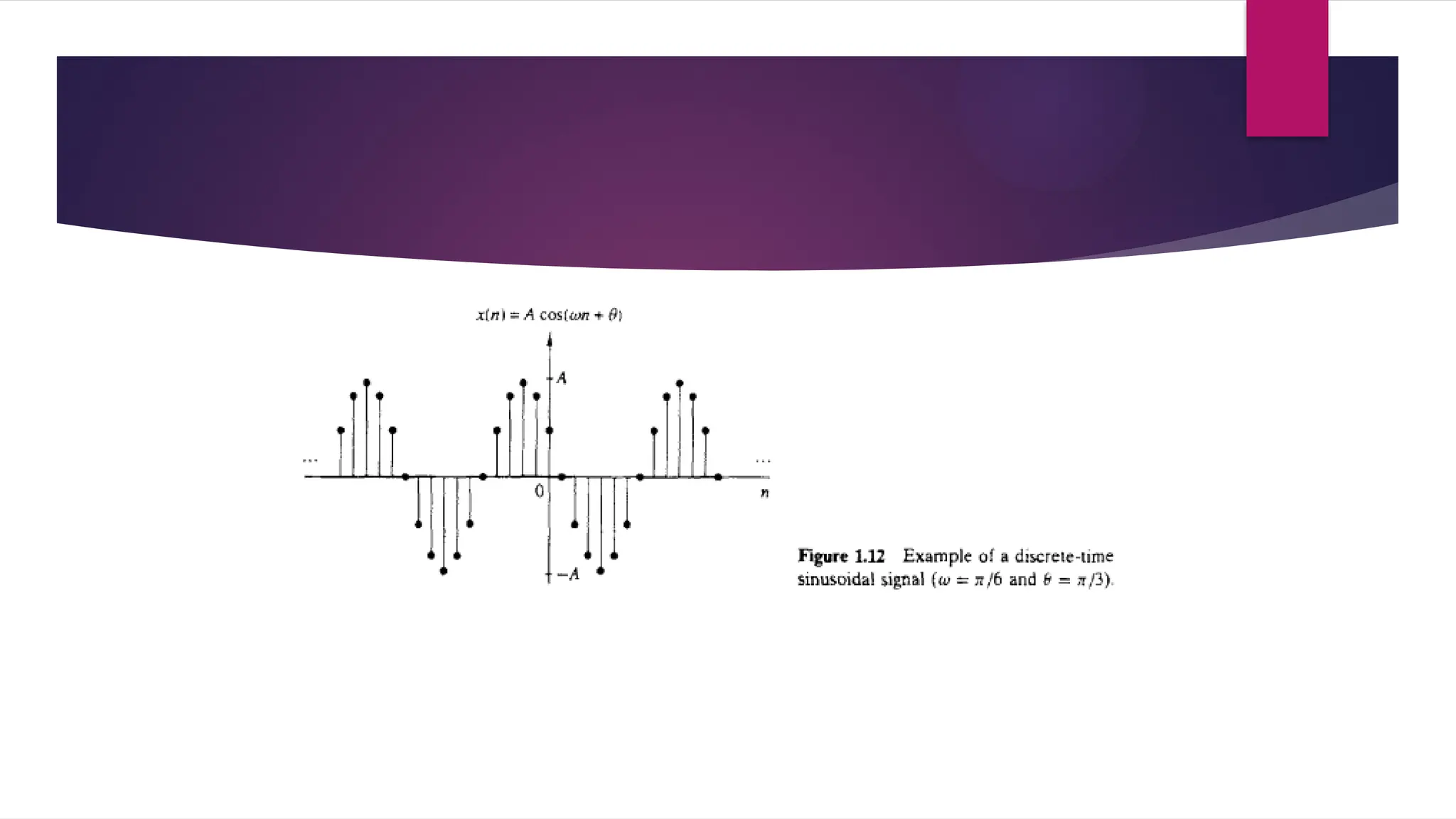
The document outlines the principles and elements of digital signal processing, including definitions of signals, systems, and the processes involved in filtering and processing signals. It differentiates between analog and digital signal processing, highlighting the advantages of digital systems, such as improved accuracy and ease of storage. Additionally, it classifies signals into various types, such as continuous versus discrete, deterministic versus random, and introduces key concepts like sampling and quantization.

1. Digital Signal Processing
 COURSE CODE: BEC502
 CREDITS: 4
 TEACHING HOURS/WEEK(L:T:P:S)= 3:0:2:0

2. Signals, System and Signal Processing
 Signal: A signal is the variation of physical quantity with respect to one or more
independent variable.
 It varies with time, space, or any other independent variables.
 It is a function which carries some information.

3. Examples
 S(t) = 5t,
The function varies linearly with the independent variable, t (time)
 S (x, y) = 3x + 2xy + 10y2
,
Two independent variables, x, y.

4. Characteristics of Signals
 A sign wave has three characteristics:
 Amplitude
 Frequency or period
 Phase
Where,
Ai (t)= Amplitude, Fi (t)=Frequency,i(t)=Phase
෍ 𝐴
𝑖ሺ
𝑡ሻ𝑆
𝑖𝑛[2𝜋
𝐹
𝑖ሺ
𝑡ሻ𝑡+ 𝜃𝑖(𝑡)]
𝑁
𝑖=1

5. System
 A physical device that performs an operation on signal.
 Example: Filters.
 A filter used to reduce the noise and interference corrupting a desired information-bearing
signal is called a system.

6. Signal Processing
 When we pass a signal through a system, as in filtering, we say that we have processed
the signal. In this case the processing of the signal involves filtering the noise and
interference from the desired signal.
 In general, the system is characterized by the type of operation that it performs on the
signal. Such operations are usually referred to as signal processing.

7. Basic Elements of a Digital Signal
Processing
System
Analog input signal Analog output signal
Fig: Analog Signal Processing
Analog Signal
Processing

8. Block Diagram of a Digital Signal Processing
A/D
Converter
Digital Signal
Processor
D/A Converter
Analog Input
signal
Analog output
signal
Digital Input
signal
Digital Output
signal
Fig: Block Diagram of a digital signal processing

9. Advantages of digital over analog signal processing
 Digital signal processing operations can be changed by changing the program in digital programmable
 Better control of accuracy in digital systems compared to analog systems.
 Digital signals are easily stored on magnetic media such as magnetic tape without loss of quality of reproduction of
signal.
 Digital signals can be processed off line, i.e., these are easily transported.
 Sophisticated signal processing algorithms can be implemented by DSP method.
 Digital circuits are less sensitive to tolerances of component values.
 Digital systems are independent of temperature, ageing and other external parameters.
 Digital circuits can be reproduced easily in large quantities at comparatively lower cost..
 Processor characteristics during processing, as in adaptive filters can be easily adjusted in digital implementation.

10. Classification of Signals
 Multichannel and Multidimensional signals
 Continuous-Time versus Discrete-Time signals
 Continuous-Valued versus Discrete-Valued Signals
 Deterministic versus Random signals

11. Multichannel and Multidimensional signals
 Multichannel Signals:
 Signals which are generated by multiple sources or multiple sensors are called multichannel signals.
 These signals are represented by vector
S(t) = [(S1(t) S2(t) S3 (t)]
Above signal represents a 3-channel signal.
 Multidimensional signals:
 A signal is called multidimensional signal if it is a function of M independent variables.
 For example : Speech signal is a one dimensional signal because amplitude of signal depends upon
single independent variable, namely, time.

12. Continuous-Time Signals
 Defined for every values of time.
 Take on values in the continuous interval ( a, b)
where, a can be -∞ and b can be ∞
 Function of a continuous variable
 Example: x (t) = sinπt

13. Discrete-Time Signal
 Defined only at discrete instants of time.
 A discrete-time sinusoidal signal may be expressed as,
X(n) = --------------(1)
where, n = Integer variable, A= Amplitude,
= Frequency in radians/sample, = Phase in radian.
So the equation (1) becomes,
X(n) =,

14. Continuous-Valued Signals versus
Discrete-Valued signals
 If a signal tak es on all possible values on a finite or an infinite range, itis
said to be continuous valued signal.
 Alternatively , if the signal takes on values from a finite set of possible
values, it is said to be a discrete-valued signal.
 A discrete-time signal having a set of discrete values is called a digital
signal.

15.  Sampling: Conversion of a continuous- time signal into a discrete-time signal obtained
by taking “samples” of the continuous-time signal at discrete-time instants.
 Now,
X(n) =
= Here, T= Sampling Interval= 1/Fs for sample
=
=
Where, F= Fundamental Frequency= cycles/s
Fs= Sampling Frequency= samples/s
f= Normalized frequency= cycles/ samples

17. Digital Signal
 Quantization: Conversion of a discrete-time continuous-valued signal into a discrete-time,
discrete-valued (Digital) signal.
5.6 7.2 8.3 9.6
6 7 8 10  sampling, quantized value
5.6-6= -0.4 7.2-7= 0.2 8.3-8= 0.3 9.6-10= -0.4
Quantization Error Quantization Error

18. Deterministic Versus Random Signals
 Any signal that can be uniquely described by an explicit mathematical expression ,a table
of data , or a well-defined rule is called deterministic.
 This term is used to emphasize the fact that all past, present, and future values o f the
signal are known precisely, without any uncertainity .
 There are signals that either cannot be described to any reasonable degree of accuracy
by explicit mathematical formulas, o r such a description is too complicated to be of any
practical use. The lack of such a relationship implies tha t such signals evolve in time in an
unpredictable manner. We refer to these signals as random . The output of a noise
generator,the seismic signal , and th e speech signal are examples of random signals.

19. THE CONCEPT OF FREQUENCY IN CONTINUOUS-TIME AND
DISCRETE-TIME SIGNALS
1)Continuous-Time Sinusoidal Signals
 A simple harmonic oscillation is mathematically described by the follow ing continuous-time
sinusoidal signal:
 The subscript a used with x(t)denotes an analog signal.
 This signal is completely characterized by three parameters: A is the amplitude of the
 sinusoid. Ω is the frequency in radians per second (rad/s), and θ is the phase in
 radians. Instead of Ω, we often use the frequency F in cycles per second or hertz
 (H z), where
Ω =2πF
In term s of F can be written as

20.  W e will use both forms, in representing sinusoidal signals.

21. The analog sinusoidal signal is characterized by the following properties:
A1: For every fixed value of the frequency F, xa(t) is periodic. Indee d , it can
easily be shown, using elementary trigonometry , that
x a(t + Tp ) = xa(t)
where Tp = 1/F is the fundamental period of the sinusoidal signal.
A 2. Continuous-time sinusoidal signals with distinct(different) frequencies are
themselves distinct.
A 3. Increasing the frequency F results in an increase in the rate of oscillation
of the signal, in the sense that more periods are included in a given time
interval.

22. The relationships we have described for sinusoidal signals carry over to the
class of complex exponential signals
This can easily be seen by expressing these signals in terms of sinusoids using the
Euler identity

23. Discrete Time Sinusoidal Signal
A discrete-time sinusoidal signal may be expressed as
where n is an integer variable, called the sample number. A is the amplitude of the
sinusoid, ω is the frequency in radians per sample, and θ is the phase in radians.
If instead of ω we use the frequency variable f defined by
ω=2πf
the relation
becomes

25. properties


26.  Sin(.1)= = =
 Sin(.2)=
 Problem: Sin() , find fundamental period.
Solution:
L.C.M= 20
So, N= 20 (Fundamental Period).
 Discrete-time sinusoids whose frequencies are separated by an integer multiple of 2.

27.  B 3. The highest rate o f oscillation in a discrete-time sin u s o id is attained
when ω=π or(ω=-π) or equivalently, f=1/2 or(f=-1/2)
 To illustrate this property , let us investigate the characteristics of the
sinusoidal signal sequence
w hen the freq u e n cy varies from 0 to π .
To simplify the argument, we take values of (ωo = 0, π/8, π/4 , π/2 , π corresponding to f=
0, 1/16,1/8,1/4,1/2 which result in periodic sequences having periods N = ∞,16, 8, 4, 2. as
depicted in Fig..
We note that the period of the sinusoid decreases as the frequency increases.
In fact,we can see that the rate o f oscillation increases as the frequency increases.

29. Discrete Time Signal & System
 Functional Representation:
 Sequence Representation:
1, for n=1,3
x(n)=4, for n=2
0, elsewhere
x(n)= {1, 2, -1, 3, -2, 1}

30. Some Elementary Discrete-time Signal
 Unit Sample Sequence/Unit Impulse Response: It is denoted by where,
= 1, for n
0, for n
 Unit Step signal: It is denoted by u where,
u(n)= 1, for n 0
0, for n

31.  Unit ramp signal: It is denoted by ur(n) where,
ur(n)= n, for n
0, for n< 0
 The exponential signal:
x(n) = an

34. Classification of Discrete-time Signal
 Energy Signals: The energy E of a signal x(n) is defined by,
 The energy of a signal can be finite or infinite.
 If E is finite (0 < E < ), then x(n) is called an energy signal.
 Power Signals: The average power of a discrete-time signal x(n) is defined by,
P=

35.  If we define the signal energy of x(n) over the finite interval -Nn as,
Then the signal energy E is,
E
and The average power of the signal x(n) is,
P=

36. Periodic signals and aperiodic signals.
 A signal x(n) is periodic with period N ( N > 0) if and only if
x(n+N)=x(n) for all n
The smallest value of N for which the above eqn holds is called the
(fundamental) period.
 If there is no value of N that satisfies above eqn, the signal is called
nonperiodic or aperiodic.

37. Symmetric (even) and antisymmetric
(odd) signals.
 A real valued signal x(n) is called symmetric (even) if
x(-n)=x(n)
 On the other hand , a signal x( n ) is called antisymmetric (odd) if
x(-n)=-x(n)

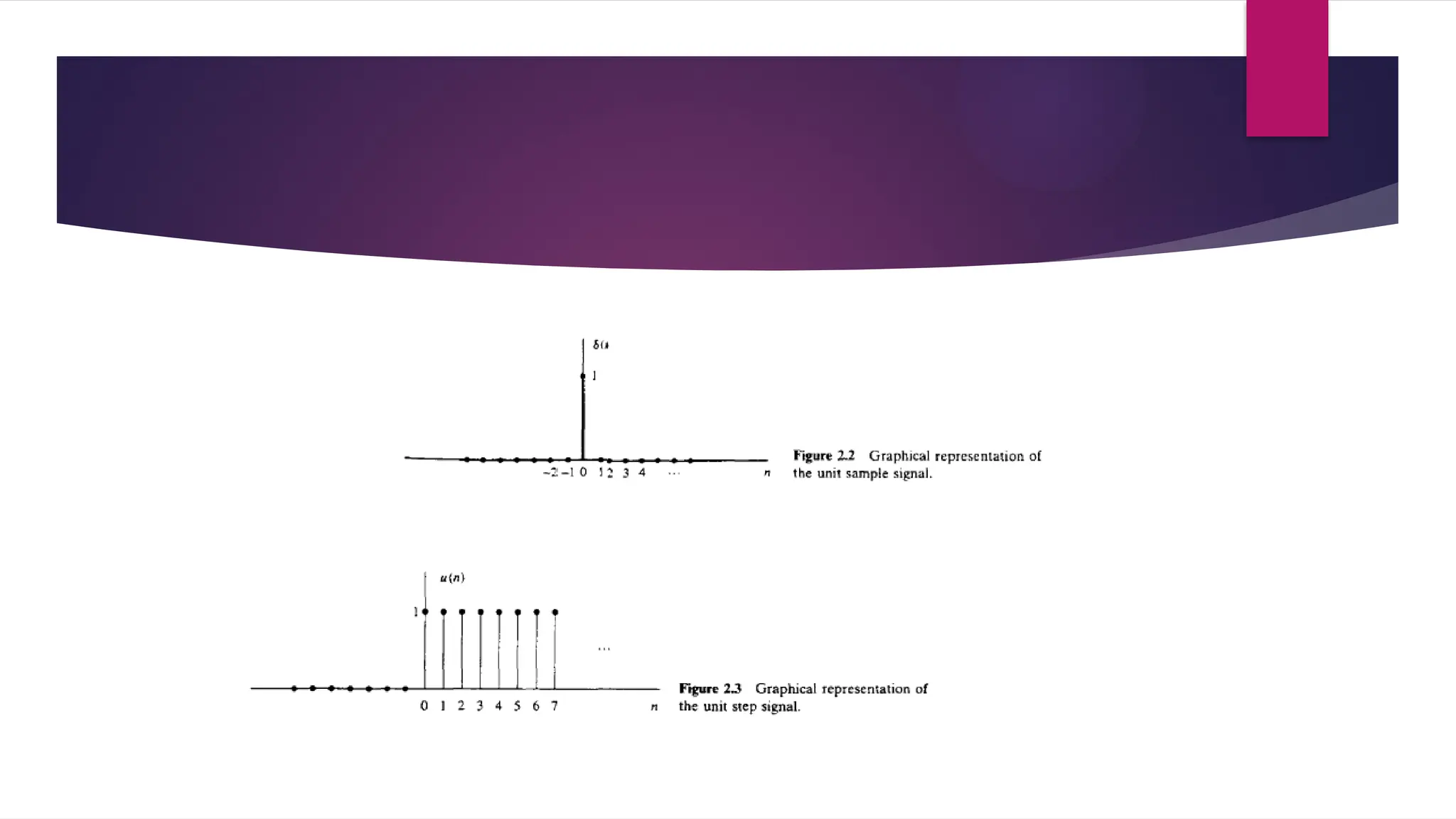
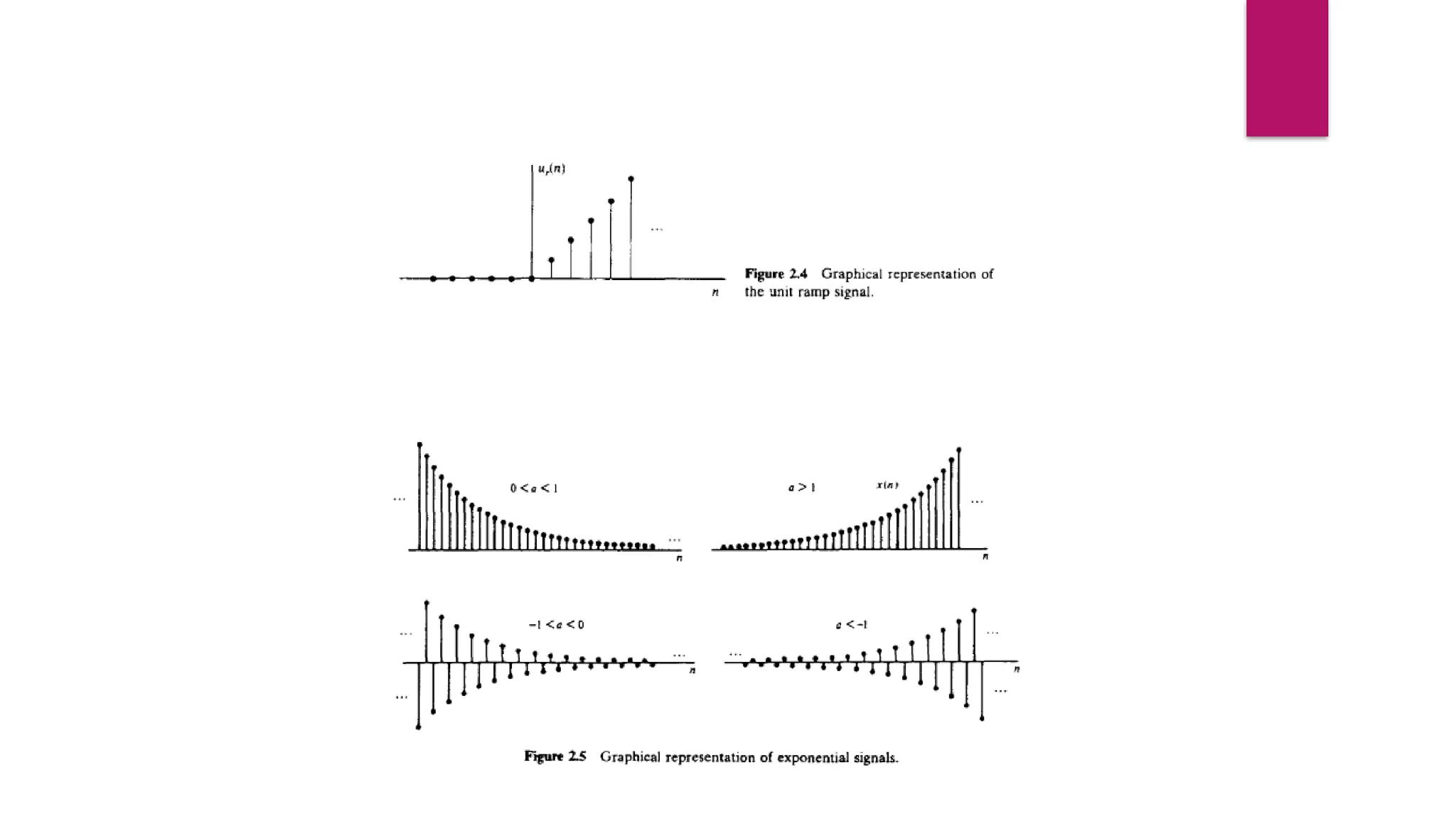
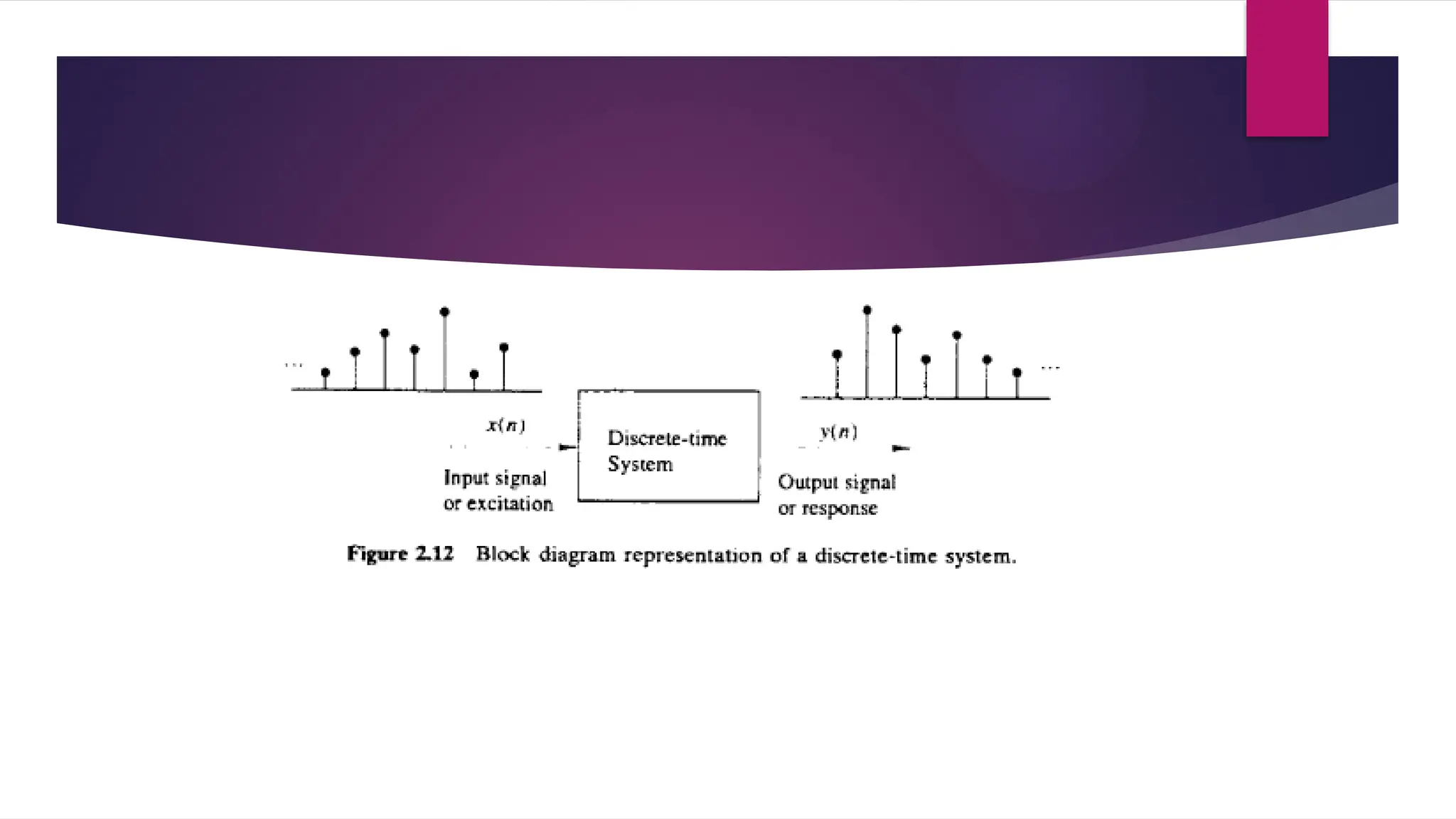
38. DISCRETE-TIME SYSTEMS
 A discrete-time system is a device or algorithm that operates on a discrete -time
signal,called the input or excitation, according to some well-defined rule, to
produce an other discrete-tim e signal called the output or response of the
system .
In general,
 We view a system as an operation or a set of operations performed on the input
signal x(n) to produce the output signal y(n). We say that the input signal x(n) is
transformed by the system in to a signal y(n), and express the general
relationship between x(n) and y(n) as
y(n)=Τ[x(n)]
 where the symbol T denotes th e transformatio n (also called an operator), or
processing performed by the system on x(n) to produce y(n).

40. Block Diagram Representation of
Discrete-Time Systems
 An adder. Figure illustrates a system (adder) that performs the addition of
two signal sequences to form another (the sum) sequence, which we
denote